Ground-breaking on the way to a new experiment at Fermilab to look for the neutrinoless transformation of a muon into an electron.

Image credit, top: Reidar Hahn/Fermilab.
The Mu2e experiment at Fermilab recently achieved an important milestone, when it received the US Department of Energy’s critical-decision 2 (CD-2) approval in March. This officially sets the baselines in the scope, cost and schedule of the experiment. At the same time, the Mu2e collaboration was awarded authorization to begin fabricating one of the experiment’s three solenoids and to begin the construction of the experimental hall, which saw ground-breaking on 18 April (figure 1). The experiment will search with unprecedented sensitivity for the neutrinoless conversion of a muon into an electron.
Some history
The muon was first observed in 1937 in cosmic-ray interactions. The implications of this discovery, which took decades of additional progress in both experiment and theory to reveal, were profound and ultimately integral to the formulation of the Standard Model. Among the cornerstones of the model are symmetries in the underlying mathematics and the conservation laws they imply. This connection between theory (the mathematical symmetries) and experiment (the measurable conservation laws) was formalized by Emmy Noether in 1918, and is fundamental to particle physics. For example, the mathematics describing the motion of a system of particles gives the same answer regardless of where in the universe this system is placed. In other words, the equations of motion are symmetric, or invariant, to translations in space. This symmetry manifests itself as the conservation of momentum. A similar symmetry to translations in time is responsible for the conservation of energy. In this way, in particle physics, observations of conserved quantities offer important insights into the underlying mathematics that describe nature’s inner workings. Conversely, when a conservation law is broken, it often reveals something important about the underlying physics.
The implications of neutrino mixing have yet to be revealed fully.
In the Standard Model there are three families of quarks and three families of leptons. Generically speaking, members of the same family interact preferentially with one another. However, it has long been known that quark families mix. The Cabibbo–Kobayashi–Maskawa matrix characterizes the degree to which a particular quark interacts with quarks of a different family. This phenomenon has profound implications, and plays a role in the electroweak interactions that power the Sun and in the origin of CP violation. For decades it appeared that the lepton family did not mix: the lepton family number was always conserved in experiments. This changed with the observation that neutrinos mix (Fukuda et al. 1998, Ahmad et al. 2001). This discovery has profound implications; for example, neutrinos must have a finite mass, which requires the addition of a new field or a new interaction to the original Standard Model – the updated Standard Model is sometimes denoted the νSM. Indeed, the implications of neutrino mixing have yet to be revealed fully, and a vigorous worldwide experimental programme is aimed at further elucidating the physics underlying this phenomena. As often happens in science, the discovery of neutrino oscillations gave rise to a whole new set of questions. Among them is this: if the quarks mix, and the neutral leptons (the neutrinos) mix, what about the charged leptons?
A probe of new physics
Searches for charged-lepton flavour violation (CLFV) have a long history in particle physics. When the muon was discovered, one suggestion was that it might be an excited state of the electron, and so experiments searched for μ → eγ decays (Hicks and Pontecorvo 1948, Sard and Althaus 1948). The non-observation of this reaction, and the subsequent realization that there are two distinct neutrinos produced in traditional muon decay, led physicists to conclude that the muon was a new type of lepton, distinct from the electron. This was an important step along the way to formulating a theory that included several families of leptons (and, eventually, quarks). Nevertheless, searches for CLFV have continued ever since, and it is easy to understand why. In the Standard Model, with massless neutrinos, CLFV processes are strictly forbidden. Therefore, any observation of a CLFV decay would signal unambiguous evidence of new physics beyond the Standard Model. Today, even with the introduction of neutrino mass, the situation is not significantly different. In the νSM, the rate of CLFV decays is proportional to [Δm2ij/M2W]2, where Δm2ij is the mass-squared difference between the ith and jth neutrino, and MW is the mass of the W boson. The predicted rates are therefore in the region of 10–50 or smaller – far below any experimental sensitivity currently conceivable. Therefore, it remains the case that any observation of a CLFV interaction would be a discovery of new physics.
The case for pursuing CLFV searches is compelling. A wide variety of models of new physics predict large enhancements relative to the νSM (30–40 orders of magnitude) for CLFV interactions. Extra dimensions, little Higgs, lepto quarks, heavy neutrinos, grand unified theories, and all variety of supersymmetric models predict CLFV rates to which upcoming experiments will have sensitivity (see, for example, Mihara et al. 2013). Importantly, ratios of various CLFV interactions can discriminate among the different models and offer insights into the underlying new physics complementary to what experiments at the LHC, neutrino experiments, or astroparticle-physics endeavours can accomplish.
The most constraining limits on CLFV come from μ → eγ muon-to-electron conversion, μ → 3e, K → ll’, and τ decays. In the coming decade the largest improvements in sensitivity will come from the muon sector. In particular, there are plans for dramatic improvements in sensitivity for the muon-to-electron conversion process, in which the muon converts directly to an electron in the presence of a nearby nucleus with no accompanying neutrinos, μ–N → e–N. The presence of the nucleus is required to conserve energy and momentum. The process is a coherent one and, apart from receiving a small recoil energy, the nucleus is unchanged from its initial state. The Mu2e experiment at Fermilab (Bartoszek et al. 2015) and the COMET experiment at the Japan Proton Accelerator Research Complex (Cui et al. 2009) both aim to improve the current state-of-the-art by a factor of 10,000, starting in the next five years.
The Mu2e experiment
The Mu2e experiment will use the existing Fermilab accelerator complex to take 8-GeV protons from the Booster, rebunch them in the Recycler, and slow-extract them to the experimental apparatus from the Muon Campus Delivery Ring, which was formerly the anti-proton Accumulator/Debuncher ring for the Tevatron. Mu2e will collect about 4 × 1020 protons on target, resulting in about 1018 stopped muons, which will yield a single-event sensitivity for μ–N → e–N of 2.5 × 10–17 relative to normal muon nuclear capture (μ–N → νμN´). The expected background yield over the full physics run is estimated to be less than half an event. This gives an expected sensitivity of 6 × 10–17 at 90% confidence level and a discovery sensitivity of 5σ to all conversion rates larger than about 2 × 10–16. For comparison, many of the new-physics models discussed above predict rates as large as 10–14, which would yield hundreds of signal events. This projected sensitivity is 10,000 times better than the world’s current best limit (Bertl et al. 2006), and will probe effective mass scales for new physics up to 104 TeV/c2, well beyond what experiments at the LHC can explore directly.
The Mu2e experimental concept is simple. Protons interact with a primary target to create charged pions, which are focused and collected by a magnetic field in a volume where they decay to yield an intense source of muons. The muons are transported to a stopping target, where they slow, stop and are captured in atomic orbit around the target nuclei. Mu2e will use an aluminium stopping target: the lifetime of the muon in atomic orbit around an aluminium nucleus is 864 ns. The energy of the electron from the CLFV interaction μ–N → e–N – given by the mass of the muon less the atomic binding energy and the nuclear recoil energy – is 104.96 MeV. Because the nucleus is left unchanged, the experimental signature is a simple one – a mono-energetic electron and nothing else. Active detector components will measure the energy and momentum of particles originating from the stopping target and discriminate signal events from background processes.
Because the signal is a single particle, there are no combinatorial backgrounds, a limiting factor for other CLFV reactions. The long lifetime of the muonic-aluminium atom can be exploited to suppress prompt backgrounds that would otherwise limit the experimental sensitivity. While the energy scale of the new physics that Mu2e aims to explore is at the tera-electron-volt level, the physical observables are at much lower energy. In Mu2e, 100 MeV is considered “high energy”, and the vast majority of background electrons are at energies < Mμ/2 ~ 53 MeV.

Image credit: Reidar Hahn/Fermilab.
Mu2e’s dramatic increase in sensitivity relative to similar experiments in the past is enabled by two important improvements in experimental technique: the use of a solenoid in the region of the primary target and the use of a pulsed proton beam. Currently, the most intense stopped-muon source in the world is at the Paul Scherrer Institut in Switzerland, where they achieve more than 107 stopped-μ−/s using about 1 MW of protons. Using a concept first proposed some 25 years ago (Dzhilkibaev and Lobashev 1989), Mu2e will place the primary production target in a solenoidal magnetic field. This will cause low-energy pions to spiral around the target where many will decay to low-energy muons, which then spiral down the solenoid field and stop in an aluminium target. This yields a very efficient muon beamline that is expected to deliver three-orders-of-magnitude-more stopped muons per second than past facilities, using only about 1% of the proton beam power.
A muon beam inevitably contains some pions. A pulsed beam helps to control a major source of background from the pions. A low-energy negative pion can stop in the aluminium target and fall into an atomic orbit. It annihilates very rapidly on the nucleus, producing an energetic photon a small percentage of the time. These photons can create a 105 MeV electron through pair production in the target, which can, in turn, fake a conversion electron. Pions at the target must be identified to high certainty or be eliminated. With a pulsed muon beam, the search for conversion electrons is delayed until almost all of the pions in the beam have decayed or interacted. The delay is about 700 ns, while the search period is about 1-μs long. The lifetime of muonic aluminium is long enough that most of the signal events occur after the initial delay. To prevent pions from being produced and arriving at the aluminium target during the measurement period, the beam intensity between pulses must be suppressed by 10 orders of magnitude.
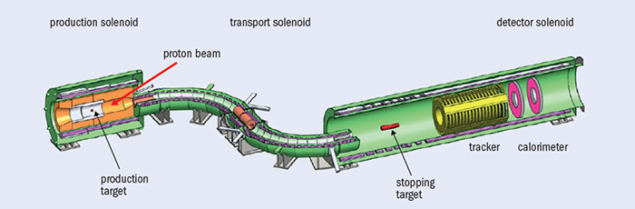
The Mu2e apparatus consists of three superconducting solenoids connected in series (figure 2). Protons arriving from the upper right strike a tungsten production target in the middle of the production solenoid. The resulting low-energy pions decay to muons, some of which spiral downstream through the “S”-shaped transport solenoid (TS) to the detector solenoid (DS), where they stop in an aluminium target. A strong negative magnetic-field gradient surrounding the production target increases the collection efficiency and improves muon throughput in the downstream direction. The curved portions of the TS, together with a vertically off-centre collimator, preferentially transmit low-momentum negative particles. A gradient surrounding the stopping target reflects some upstream-spiralling particles, improving the acceptance for conversion electrons in the detectors.
When a muon stops in the aluminium target, it emits X-rays while cascading through atomic orbitals to the 1s level. It then has 61% probability of being captured by the nucleus, and 39% probability of decaying without being captured. In the decay process, the distribution of decay electrons largely follows the Michel spectrum for free muon decay, and most of the electrons emitted have energies below 53 MeV. However, the nearby nucleus can absorb some energy and momentum, with the result that, with low probability, there is a high-energy tail in the electron distribution reaching all of the way to the conversion-electron energy, and this poses a potential background. Because the probability falls rapidly with increasing energy, this background can be suppressed with sufficiently good momentum resolution (better than about 1% at 105 MeV/c).
Detector components
Inside the DS, particles that originate from the stopping target are measured in a straw-tube tracker followed by a barium-fluoride (BaF2) crystal calorimeter array. The inner radii of the tracker and calorimeter are left un-instrumented, so that charged particles with momenta less than about 55 MeV/c, coming from the beamline or from Michel decays in the stopping target, have low transverse momentum and spiral downstream harmlessly.
The tracker is 3-m long with inner and outer active radii of 39 cm and 68 cm, respectively. It consists of about 20,000 straw tubes 5 mm in diameter, which have 15-μm-thick mylar walls and range in length from 0.4–1.2 m (figure 3). They are oriented perpendicular to the solenoid axis. Conversion-electron candidates make between two and three turns of the helix in the 3-m length. The tracker provides better than 1 MeV/c (FWHM) resolution for 105 MeV/c electrons.
The final solenoid commissioning is scheduled to begin in 2019.
Situated immediately behind the tracker, the calorimeter provides sufficient energy and timing resolution to separate muons and pions from electrons with energy around 100 MeV. The BaF2 crystals have a fast component (decay time around 1 ns) that makes the Mu2e calorimeter tolerant of high rates without significantly affecting the energy or timing resolutions. Surrounding the DS and half the TS is a four-layer scintillator system that will identify through-going cosmic rays with 99.99% efficiency. A streaming data acquisition (DAQ) architecture will handle about 70 GB of data a second when beam is present. A small CPU farm will provide an online software trigger to reduce the accept rate to about 2 kHz. A dedicated detector system will monitor the suppression of out-of-time protons, while another will determine the number of stopped muons.
Having cleared the CD-2 milestone in March, the Mu2e collaboration is now focused on clearing the next hurdle – a CD-3 “construction readiness” review in early 2016. In preparation, prototypes of the tracker, calorimeter, cosmic-ray veto, DAQ and other important components are being built and tested. In addition, the fabrication of 27 coil modules that make up the “S” of the transport solenoid will begin soon, and the building construction will continue into 2016. The final solenoid commissioning is scheduled to begin in 2019, while detector and beamline commissioning are scheduled to begin in 2020.





