Do muons wobble faster than expected?

Fundamental charged particles have spins that wobble in a magnetic field. This is just one of the insights that emerged from the equation Paul Dirac wrote down in 1928. Almost 100 years later, calculating how much they wobble – their “magnetic moment” – strains the computational sinews of theoretical physicists to a level rarely matched. The challenge is to sum all the possible ways in which the quantum fluctuations of the vacuum affect their wobbling.

The particle in question here is the muon. Discovered in cosmic rays in 1936, muons are more massive but ephemeral cousins of the electron. Their greater mass is expected to amplify the effect of any undiscovered new particles shimmering in the quantum haze around them, and measurements have disagreed with theoretical predictions for nearly 20 years. This suggests a possible gap in the Standard Model (SM) of particle physics, potentially providing a glimpse of deeper truths beyond it.

In the coming weeks, Fermilab is expected to present the final results of a seven-year campaign to measure this property, reducing uncertainties to a remarkable one part in 10¹⁰ on the magnetic moment of the muon, and 0.1 parts per million on the quantum corrections. Theorists are racing to match this with an updated prediction of comparable precision. The calculation is in good shape, except for the incredibly unusual eventuality that the muon briefly emits a cloud of quarks and gluons at just the moment it absorbs a photon from the magnetic field. But in quantum mechanics all possibilities count all the time, and the experimental precision is such that the fine details of “hadronic vacuum polarisation” (HVP) could be the difference between reinforcing the SM and challenging it.

Quantum fluctuations

The Dirac equation predicts that fundamental spin s = ½ particles have a magnetic moment given by g(eħ/2m)s, where the gyromagnetic ratio (g) is precisely equal to two. For the electron, this remarkable result was soon confirmed by atomic spectroscopy, before more precise experiments in 1947 indicated a deviation from g = 2 of a few parts per thousand. Expressed as a = (g-2)/2, the shift was a surprise and was named the magnetic anomaly or the anomalous magnetic moment.

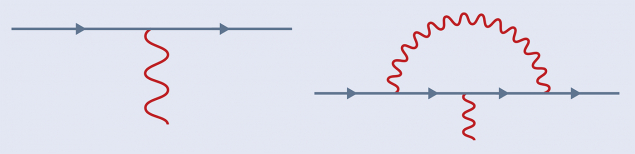
This marked the beginning of an enduring dialogue between experiment and theory. It became clear that a relativistic field theory like the developing quantum electrodynamics (QED) could produce quantum fluctuations, shifting g from two. In 1948, Julian Schwinger calculated the first correction to be a = α/2π ≈ 0.00116, aligning beautifully with 1947 experimental results. The emission and absorption of a virtual photon creates a cloud around the electron, altering its interaction with the external magnetic field (see “Quantum fluctuation” figure). Soon, other particles would be seen to influence the calculations. The SM’s limitations suggest that undiscovered particles could also affect these calculations. Their existence might be revealed by a discrepancy between the SM prediction for a particle’s anomalous magnetic moment and its measured value.

As noted, the muon is an even more promising target than the electron, as its sensitivity to physics beyond QED is generically enhanced by the square of the ratio of their masses: a factor of around 43,000. In 1957, inspired by Tsung-Dao Lee and Chen-Ning Yang’s proposal that parity is violated in the weak interaction, Richard Garwin, Leon Lederman and Marcel Weinrich studied the decay of muons brought to rest in a magnetic field at the Nevis cyclotron at Columbia University. As well as showing that parity is broken in both pion and muon decays, they found g to be close to two for muons by studying their “precession” in the magnetic field as their spins circled around the field lines.

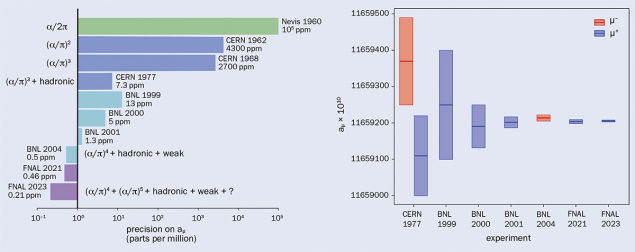
This iconic experiment was the prototype of muon-precession projects at CERN (see CERN Courier September/October 2024 p53), later at Brookhaven National Laboratory and now Fermilab (see “Precision” figure). By the end of the Brookhaven project, a disagreement between the measured value of “a_μ” – the subscript indicating g-2 for the muon rather than the electron – and the SM prediction was too large to ignore, motivating the present round of measurements at Fermilab and rapidly improving theory refinements.

g-2 and the Standard Model

Today, a prediction for a_μ must include the effects of all three of the SM’s interactions and all of its elementary particles. The leading contributions are from electrons, muons and tau leptons interacting electromagnetically. These QED contributions can be computed in an expansion where each successive term contributes only around 1% of the previous one. QED effects have been computed to fifth order, yielding an extraordinary precision of 0.9 parts per billion – significantly more precise than needed to match measurements of the muon’s g-2, though not the electron’s. It took over half a century to achieve this theoretical tour de force.

The weak interaction gives the smallest contribution to a_μ, a million times less than QED. These contributions can also be computed in an expansion. Second order suffices. All SM particles except gluons need to be taken into account.

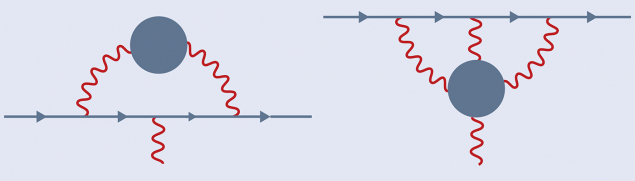
Gluons are responsible for the strong interaction and appear in the third and last set of contributions. These are described by QCD and are called “hadronic” because quarks and gluons form hadrons at the low energies relevant for the muon g-2 (see “Hadronic contributions” figure). HVP is the largest, though 10,000 times smaller than the corrections due to QED. “Hadronic light-by-light scattering” (HLbL) is a further 100 times smaller due to the exchange of an additional photon. The challenge is that the strong-interaction effects cannot be approximated by a perturbative expansion. QCD is highly nonlinear and different methods are needed.

Data or the lattice?

Even before QCD was formulated, theorists sought to subdue the wildness of the strong force using experimental data. In the case of HVP, this triggered experimental investigations of e⁺e^– annihilation into hadrons and later hadronic tau–lepton decays. Though apparently disparate, the production of hadrons in these processes can be related to the clouds of virtual quarks and gluons that are responsible for HVP.

A more recent alternative makes use of massively parallel numerical simulations to directly solve the equations of QCD. To compute quantities such as HVP or HLbL, “lattice QCD” requires hundreds of millions of processor-core hours on the world’s largest supercomputers.

In preparation for Fermilab’s first measurement in 2021, the Muon g-2 Theory Initiative, spanning more than 120 collaborators from over 80 institutions, was formed to provide a reference SM prediction that was published in a 2020 white paper. The HVP contribution was obtained with a precision of a few parts per thousand using a compilation of measurements of e⁺e^– annihilation into hadrons. The HLbL contribution was determined from a combination of data-driven and lattice–QCD methods. Though even more complex to compute, HLbL is needed only to 10% precision, as its contribution is smaller.

After summing all contributions, the prediction of the 2020 white paper sits over five standard deviations below the most recent experimental world average (see “Landscape of muon g-2” figure). Such a deviation would usually be interpreted as a discovery of physics beyond the SM. However, in 2021 the result of the first lattice calculation of the HVP contribution with a precision comparable to that of the data-driven white paper was published by the Budapest–Marseille–Wuppertal collaboration (BMW). The result, labelled BMW 2020 as it was uploaded to the preprint archive the previous year, is much closer to the experimental average (green band on the figure), suggesting that the SM may still be in the race. The calculation relied on methods developed by dozens of physicists since the seminal work of Tom Blum (University of Connecticut) in 2002 (see CERN Courier May/June 2021 p25).

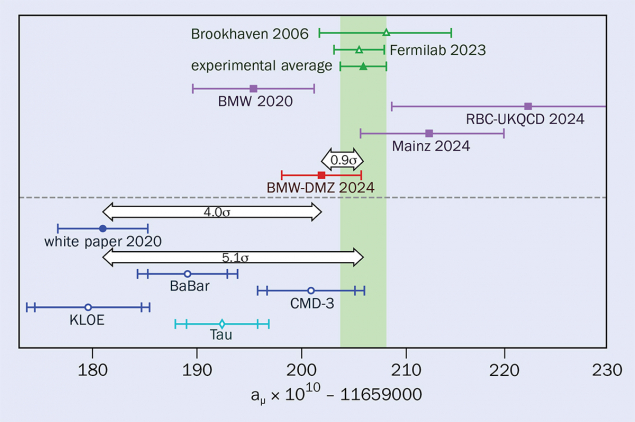
In 2020, the uncertainties on the data-driven and lattice-QCD predictions for the HVP contribution were still large enough that both could be correct, but BMW’s 2021 paper showed them to be explicitly incompatible in an “intermediate-distance window” accounting for approximately 35% of the HVP contribution, where lattice QCD is most reliable.

This disagreement was the first sign that the 2020 consensus had to be revised. To move forward, the sources of the various disagreements – more numerous now – and the relative limitations of the different approaches must be understood better. Moreover, uncertainty on HVP already dominated the SM prediction in 2020. As well as resolving these discrepancies, its uncertainty must be reduced by a factor of three to fully leverage the coming measurement from Fermilab. Work on the HVP is therefore even more critical than before, as elsewhere the theory house is in order: Sergey Volkov (KITP) recently verified the fifth-order QED calculation of Tatsumi Aoyama, Toichiro Kinoshita and Makiko Nio, identifying an oversight not numerically relevant at current experimental sensitivities; new HLbL calculations remain consistent; and weak contributions have already been checked and are precise enough for the foreseeable future.

News from the lattice

Since BMW’s 2020 lattice results, a further eight lattice-QCD computations of the dominant up-and-down-quark (u + d) contribution to HVP’s intermediate-distance window have been performed with similar precision, with four also including all other relevant contributions. Agreement is excellent and the verdict is clear: the disagreement between the lattice and data-driven approaches is confirmed (see “Intermediate window” figure).

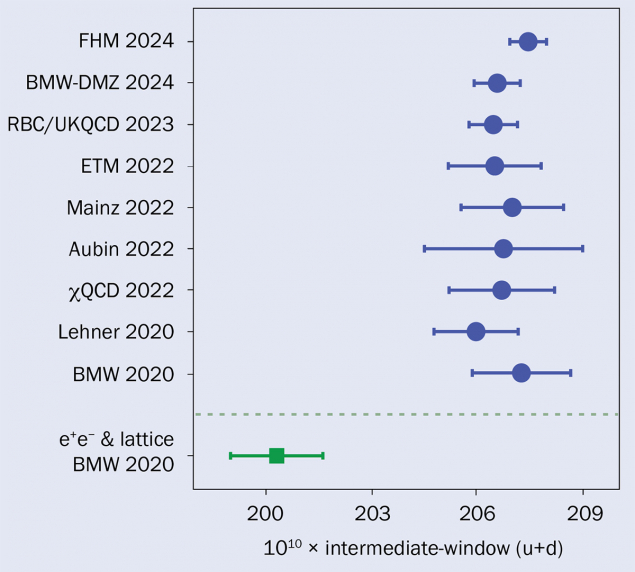
Work on the short-distance window (about 10% of the HVP contribution) has also advanced rapidly. Seven computations of the u + d contribution have appeared, with four including all other relevant contributions. No significant disagreement is observed.

The long-distance window (around 55% of the total) is by far the most challenging, with the largest uncertainties. In recent weeks three calculations of the dominant u + d contribution have appeared, by the RBC–UKQCD, Mainz and FHM collaborations. Though some differences are present, none can be considered significant for the time being.

With all three windows cross-validated, the Muon g-2 Theory Initiative is combining results to obtain a robust lattice–QCD determination of the HVP contribution. The final uncertainty should be slightly below 1%, still quite far from the 0.2% ultimately needed.

The BMW–DMZ and Mainz collaborations have also presented new results for the full HVP contribution to a_μ, and the RBC–UKQCD collaboration, which first proposed the multi-window approach, is also in a position to make a full calculation. (The corresponding result in the “Landscape of muon g-2” figure combines contributions reported in their publications.) Mainz obtained a result with 1% precision using the three windows described above. BMW–DMZ divided its new calculation into five windows and replaced the lattice–QCD computation of the longest distance window – “the tail”, encompassing just 5% of the total – with a data-driven result. This pragmatic approach allows a total uncertainty of just 0.46%, with the collaboration showing that all e⁺e^– datasets contributing to this long-distance tail are entirely consistent. This new prediction differs from the experimental measurement of a_μ by only 0.9 standard deviations.

These new lattice results, which have not yet been published in refereed journals, make the disagreement with the 2020 data-driven result even more blatant. However, the analysis of the annihilation of e⁺e^– into hadrons is also evolving rapidly.

News from electron–positron annihilation

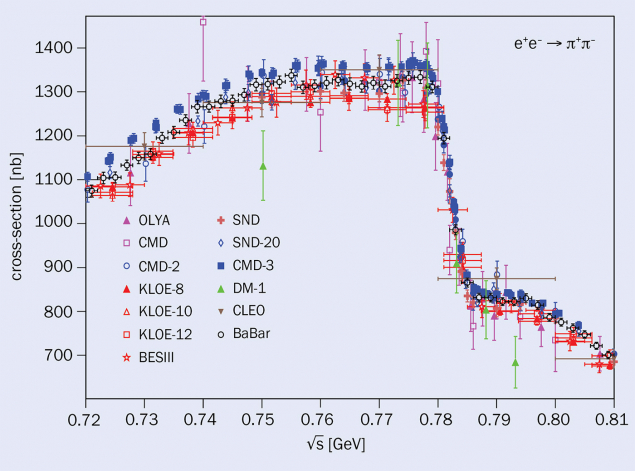
Many experiments have measured the cross-section for e⁺e^– annihilation to hadrons as a function of centre-of-mass energy (√s). The dominant contribution to a data-driven calculation of a_μ, and over 70% of its uncertainty budget, is provided by the e⁺e^– → π⁺π^– process, in which the final-state pions are produced via the ρ resonance (see “Two-pion channel” figure).

The most recent measurement, by the CMD-3 energy-scan experiment in Novosibirsk, obtained a cross-section on the peak of the ρ resonance that is larger than all previous ones, significantly changing the picture in the π⁺π^– channel. Scrutiny by the Theory Initiative has identified no major problem.

CMD-3’s approach contrasts that used by KLOE, BaBar and BESIII, which study e⁺e^– annihilation with a hard photon emitted from the initial state (radiative return) at facilities with fixed √s. BaBar has innovated by calibrating the luminosity of the initial-state radiation using the μ⁺μ^– channel and using a unique “next-to-leading-order” approach that accounts for extra radiation from either the initial or the final state – a necessary step at the required level of precision.

In 1997, Ricard Alemany, Michel Davier and Andreas Höcker proposed an alternative method that employs τ^– → π^–π⁰ν decay while requiring some additional theoretical input. The decay rate has been precisely measured as a function of the two-pion invariant mass by the ALEPH and OPAL experiments at LEP, as well as by the Belle and CLEO experiments at B factories, under very different conditions. The measurements are in good agreement. ALEPH offers the best normalisation and Belle the best shape measurement.

KLOE and CMD-3 differ by more than five standard deviations on the ρ peak, precluding a combined analysis of e⁺e^– → π⁺π^– cross-sections. BaBar and τ data lie between them. All measurements are in good agreement at low energies, below the ρ peak. BaBar, CMD-3 and τ data are also in agreement above the ρ peak. To help clarify this unsatisfactory situation, in 2023 BaBar performed a careful study of radiative corrections to e⁺e^– → π⁺π^–. That study points to the possible underestimate of systematic uncertainties in radiative-return experiments that rely on Monte Carlo simulations to describe extra radiation, as opposed to the in situ studies performed by BaBar.

The future

While most contributions to the SM prediction of the muon g-2 are under control at the level of precision required to match the forthcoming Fermilab measurement, in trying to reduce the uncertainties of the HVP contribution to a commensurate degree, theorists and experimentalists shattered a 20 year consensus. This has triggered an intense collective effort that is still in progress.

The prospect of testing the limits of the SM through high-precision measurements generates considerable impetus

New analyses of e⁺e^– are underway at BaBar, Belle II, BES III and KLOE, experiments are continuing at CMD-3, and Belle II is also studying τ decays. At CERN, the longer term “MUonE” project will extract HVP by analysing how muons scatter off electrons – a very challenging endeavour regarding the unusual accuracy required both in the control of experimental systematic uncertainties and also theoretically, for the radiative corrections.

At the same time, lattice-QCD calculations have made enormous progress in the last five years and provide a very competitive alternative. The fact that several groups are involved with somewhat independent techniques is allowing detailed cross checks. The complementarity of the data-driven and lattice-QCD approaches should soon provide a reliable value for the g-2 theoretical prediction at unprecedented levels of precision.

There is still some way to go to reach that point, but the prospect of testing the limits of the SM through high-precision measurements generates considerable impetus. A new white paper is expected in the coming weeks. The ultimate aim is to reach a level of precision in the SM prediction that allows us to fully leverage the potential of the muon anomalous magnetic moment in the search for new fundamental physics, in concert with the final results of Fermilab’s Muon g-2 experiment and the projected Muon g-2/EDM experiment at J-PARC in Japan, which will implement a novel technique.