Thanks to new theory calculations and keenly awaited measurements of the magnetic moment of the muon, a longstanding anomaly may soon be resolved either in favour of new physics or the Standard Model.

A fermion’s spin tends to twist to align with a magnetic field – an effect that becomes dramatically macroscopic when electron spins twist together in a ferromagnet. Microscopically, the tiny magnetic moment of a fermion interacts with the external magnetic field through absorption of photons that comprise the field. Quantifying this picture, the Dirac equation predicts fermion magnetic moments to be precisely two in units of Bohr magnetons, e/2m. But virtual lines and loops add an additional 0.1% or so to this value, giving rise to an “anomalous” contribution known as “g–2” to the particle’s magnetic moment, caused by quantum fluctuations. Calculated to tenth order in quantum electrodynamics (QED), and verified experimentally to about two parts in 1010, the electron’s magnetic moment is one of the most precisely known numbers in the physical sciences. While also measured precisely, the magnetic moment of the muon, however, is in tension with the Standard Model.
Tricky comparison
The anomalous magnetic moment of the muon was first measured at CERN in 1959, and prior to 2021, was most recently measured by the E821 experiment at Brookhaven National Laboratory (BNL) 16 years ago. The comparison between theory and data is much trickier than for electrons. Being short-lived, muons are less suited to experiments with Penning traps, whereby stable charged particles are confined using static electric and magnetic fields, and the trapped particles are then cooled to allow precise measurements of their properties. Instead, experiments infer how quickly muon spins precess in a storage ring – a situation similar to the wobbling of a spinning top, where information on the muon’s advancing spin is encoded in the direction of the electron that is emitted when it decays. Theoretical calculations are also more challenging, as hadronic contributions are no longer so heavily suppressed when they emerge as virtual particles from the more massive muon.
All told, our knowledge of the anomalous magnetic moment of the muon is currently three orders of magnitude less precise than for electrons. And while everything tallies up, more or less, for the electron, BNL’s longstanding measurement of the magnetic moment of the muon is 3.7σ greater than the Standard Model prediction (see panel “Rising to the moment”). The possibility that the discrepancy could be due to virtual contributions from as-yet-undiscovered particles demands ever more precise theoretical calculations. This need is now more pressing than ever, given the increased precision of the experimental value expected in the next few years from the Muon g–2 collaboration at Fermilab in the US and other experiments such as the Muon g–2/EDM collaboration at J-PARC in Japan. Hotly anticipated results from the first data run at Fermilab’s E989 experiment were released on 7 April. The new result is completely consistent with the BNL value but with a slightly smaller error, leading to a slightly larger discrepancy of 4.2σ with the Standard Model when the measurements are combined (see Fermilab strengthens muon g-2 anomaly).
Hadronic vacuum polarisation
The value of the muon anomaly, aμ, is an important test of the Standard Model because currently it is known very precisely – to roughly 0.5 parts per million (ppm) – in both experiment and theory. QED dominates the value of aμ, but due to the non-perturbative nature of QCD it is strong interactions that contribute most to the error. The theoretical uncertainty on the anomalous magnetic moment of the muon is currently dominated by so-called hadronic vacuum polarisation (HVP) diagrams. In HVP, a virtual photon briefly explodes into a “hadronic blob”, before being reabsorbed, while the magnetic-field photon is simultaneously absorbed by the muon. While of order α2 in QED, it is all orders in QCD, making for very difficult calculations.
Rising to the moment

In the Standard Model, the magnetic moment of the muon is computed order-by-order in powers of a for QED (each virtual photon represents a factor of α), and to all orders in as for QCD.
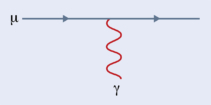
At the lowest order in QED, the Dirac term (pictured left) accounts for precisely two Bohr magnetons and arises purely from the muon (μ) and the real external photon (γ) representing the magnetic field.
At higher orders in QED, virtual Standard Model particles, depicted by lines forming loops, contribute to a fractional increase of aμ with respect to that value: the so-called anomalous magnetic moment of the muon. It is defined to be aμ = (g–2)/2, where g is the gyromagnetic ratio of the muon – the number of Bohr magnetons, e/2m, which make up the muon’s magnetic moment. According to the Dirac equation, g = 2, but radiative corrections increase its value.
The biggest contribution is from the Schwinger term (pictured left, O(α)) and higher-order QED diagrams.
aμQED = (116 584 718.931 ± 0.104) × 10–11
Electroweak lines (pictured left) also make a well-defined contribution. These diagrams are suppressed by the heavy masses of the Higgs, W and Z bosons.
aμEW = (153.6 ± 1.0) × 10–11
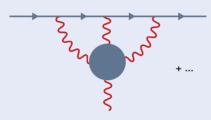
The biggest QCD contribution is due to hadronic vacuum polarisation (HVP) diagrams. These are computed from leading order (pictured left, O(α2)), with one “hadronic blob” at all orders in as (shaded) up to next-to-next-to-leading order (NNLO, O(α4), with three hadronic blobs) in the HVP.
Hadronic light-by-light scattering (HLbL, pictured left at O(α3) and all orders in αs (shaded)), makes a smaller contribution but with a larger fractional uncertainty.
Neglecting lattice–QCD calculations for the HVP in favour of those based on e+e– data and phenomenology, the total anomalous magnetic moment is given by
aμSM = aμQED + aμEW + aμHVP + aμHLbL = (116 591 810 ± 43) × 10–11.
This is somewhat below the combined value from the E821 experiment at BNL in 2004 and the E989 experiment at Fermilab in 2021.
aμexp = (116 592 061 ± 41) × 10–11
The discrepancy has roughly 4.2σ significance:
aμexp– aμSM = (251 ± 59) × 10–11.
Historically, and into the present, HVP is calculated using a dispersion relation and experimental data for the cross section for e+e– → hadrons. This idea was born of necessity almost 60 years ago, before QCD was even on the scene, let alone calculable. The key realisation is that the imaginary part of the vacuum polarisation is directly related to the hadronic cross section via the optical theorem of wave-scattering theory; a dispersion relation then relates the imaginary part to the real part. The cross section is determined over a relatively wide range of energies, in both exclusive and inclusive channels. The dominant contribution – about three quarters – comes from the e+e– → π+π– channel, which peaks at the rho meson mass, 775 MeV. Though the integral converges rapidly with increasing energy, data are needed over a relatively broad region to obtain the necessary precision. Above the τ mass, QCD perturbation theory hones the calculation.
Several groups have computed the HVP contribution in this way, and recently a consensus value has been produced as part of the worldwide Muon g–2 Theory Initiative. The error stands at about 0.58% and is the dominant part of the theory error. It is worth noting that a significant part of the error arises from a tension between the most precise measurements, by the BaBar and KLOE experiments, around the rho–meson peak. New measurements, including those from experiments at Novosibirsk, Russia and Japan’s Belle II experiment, may help resolve the inconsistency in the current data and reduce the error by a factor of two or so.
The alternative approach, of calculating the HVP contribution from first principles using lattice QCD, is not yet at the same level of precision, but is getting there. Consistency between the two approaches will be crucial for any claim of new physics.
Lattice QCD
Kenneth Wilson formulated lattice gauge theory in 1974 as a means to rid quantum field theories of their notorious infinities – a process known as regulating the theory – while maintaining exact gauge invariance, but without using perturbation theory. Lattice QCD calculations involve the very large dimensional integration of path integrals in QCD. Because of confinement, a perturbative treatment including physical hadronic states is not possible, so the complete integral, regulated properly in a discrete, finite volume, is done numerically by Monte Carlo integration.
Lattice QCD has made significant improvements over the last several years, both in methodology and invested computing time. Recently developed methods (which rely on low-lying eigenmodes of the Dirac operator to speed up calculations) have been especially important for muon–anomaly calculations. By allowing state-of-the-art calculations using physical masses, they remove a significant systematic: the so-called chiral extrapolation for the light quarks. The remaining systematic errors arise from the finite volume and non-zero lattice spacing employed in the simulations. These are handled by doing multiple simulations and extrapolating to the infinite-volume and zero-lattice-spacing limits.
The HVP contribution can readily be computed using lattice QCD in Euclidean space with space-like four-momenta in the photon loop, thus yielding the real part of the HVP directly. The dispersive result is currently more precise (see “Off the mark” figure”), but further improvements will depend on consistent new e+e– scattering datasets.
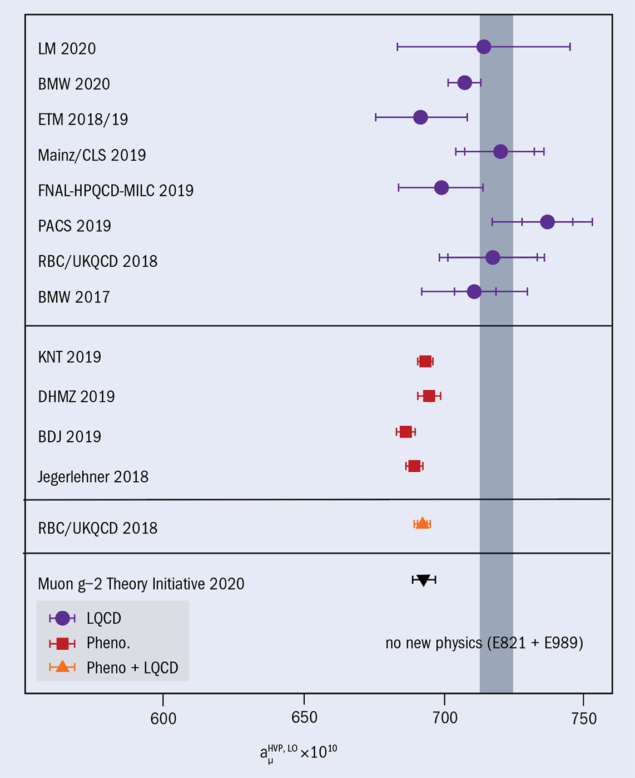
Rapid progress in the last few years has resulted in first lattice results with sub-percent uncertainty, closing in on the precision of the dispersive approach. Since these lattice calculations are very involved and still maturing, it will be crucial to monitor the emerging picture once several precise results with different systematic approaches are available. It will be particularly important to aim for statistics-dominated errors to make it more straightforward to quantitatively interpret the resulting agreement with the no-new-physics scenario or the dispersive results. In the shorter term, it will also be crucial to cross-check between different lattice and dispersive results using additional observables, for example based on the vector–vector correlators.
With improved lattice calculations in the pipeline from a number of groups, the tension between lattice QCD and phenomenological calculations may well be resolved before the Fermilab and J-PARC experiments announce their final results. Interestingly, there is a new lattice result with sub-percent precision (BMW 2020) that is in agreement both with the no-new-physics point within 1.3σ, and with the dispersive-data-driven result within 2.1σ. Barring a significant re-evaluation of the phenomenological calculation, however, HVP does not appear to be the source of the discrepancy with experiments.
The next most likely Standard Model process to explain the muon anomaly is hadronic light-by-light scattering. Though it occurs less frequently since it includes an extra virtual photon compared to the HVP contribution, it is much less well known, with comparable uncertainties to HVP.
Hadronic light-by-light scattering
In hadronic light-by-light scattering (HLbL), the magnetic field interacts not with the muon, but with a hadronic “blob”, which is connected to the muon by three virtual photons. (The interaction of the four photons via the hadronic blob gives HLbL its name.) A miscalculation of the HLbL contribution has often been proposed as the source of the apparently anomalous measurement of the muon anomaly by BNL’s E821 collaboration.
Since the so-called Glasgow consensus (the fruit of a 2009 workshop) first established a value more than 10 years ago, significant progress has been made on the analytic computation of the HLbL scattering contribution. In particular, a dispersive analysis of the most important hadronic channels has been carried out, including the leading pion–pole, sub-leading pion loop and rescattering diagrams including heavier pseudoscalars. These calculations are analogous in spirit to the dispersive HVP calculations, but are more complicated, and the experimental measurements are more difficult because form factors with one or two virtual photons are required.
The project to calculate the HLbL contribution using lattice QCD began more than 10 years ago, and many improvements to the method have been made to reduce both statistical and systematic errors since then. Last year we published, with colleagues Norman Christ, Taku Izubuchi and Masashi Hayakawa, the first ever lattice–QCD calculation of the HLbL contribution with all errors controlled, finding aμHLbL, lattice = (78.7 ± 30.6 (stat) ± 17.7 (sys)) × 10–11. The calculation was not easy: it took four years and a billion core-hours on the Mira supercomputer at Argonne National Laboratory’s Large Computing Facility.
Our lattice HLbL calculations are quite consistent with the analytic and data-driven result, which is approximately a factor of two more precise. Combining the results leads to aμHLbL = (90 ± 17) × 10–11, which means the very difficult HLbL contribution cannot explain the Standard Model discrepancy with experiment. To make such a strong conclusion, however, it is necessary to have consistent results from at least two completely different methods of calculating this challenging non-perturbative quantity.
New physics?
If current theory calculations of the muon anomaly hold up, and the new experiments reduce its uncertainty by the hoped-for factor of four, then a new-physics explanation will become impossible to ignore. The idea would be to add particles and interactions that have not yet been observed but may soon be discovered at the LHC or in future experiments. New particles would be expected to contribute to the anomaly through Feynman diagrams similar to the Standard Model topographies (see “Rising to the moment” panel).
Calculations of the anomalous magnetic moment of the muon are not finished
The most commonly considered new-physics explanation is supersymmetry, but the increasingly stringent lower limits placed on the masses of super-partners by the LHC experiments make it increasingly difficult to explain the muon anomaly. Other theories could do the job too. One popular idea that could also explain persistent anomalies in the b-quark sector is heavy scalar leptoquarks, which mediate a new interaction allowing leptons and quarks to change into each other. Another option involves scenarios whereby the Standard Model Higgs boson is accompanied by a heavier Higgs-like boson.
The calculations of the anomalous magnetic moment of the muon are not finished. As a systematically improvable method, we expect more precise lattice determinations of the hadronic contributions in the near future. Increasingly powerful algorithms and hardware resources will further improve precision on the lattice side, and new experimental measurements and analysis methods will do the same for dispersive studies of the HVP and HLbL contributions.
To confidently discover new physics requires that these two independent approaches to the Standard Model value agree. With the first new results on the experimental value of the muon anomaly in almost two decades showing perfect agreement with the old value, we anxiously await more precise measurements in the near future. Our hope is that the clash of theory and experiment will be the beginning of an exciting new chapter of particle physics, heralding new discoveries at current and future particle colliders.
Further reading
T Aoyama et al. 2020 Phys. Rept. 887 1–166.
T Blum et al. 2020 Phys. Rev. Lett. 124 132002 (arXiv:1911.08123).