Harald Fritzsch, one of the pioneers of quantum chromodynamics, recalls some of the background to the development of the theory 40 years ago.
About 60 years ago, many new particles were discovered, in particular the four Δ resonances, the six hyperons and the four K mesons. The Δ resonances, with a mass of about 1230 MeV, were observed in pion–nucleon collisions at what was then the Radiation Laboratory in Berkeley. The hyperons and K mesons were discovered in cosmic-ray experiments.
Murray Gell-Mann and Yuval Ne’eman succeeded in describing the new particles in a symmetry scheme based on the group SU(3), the group of unitary 3 × 3 matrices with determinant 1 (Gell-Mann 1962, Ne’eman 1961). SU(3)-symmetry is an extension of isospin symmetry, which was introduced in 1932 by Werner Heisenberg and is described by the group SU(2).
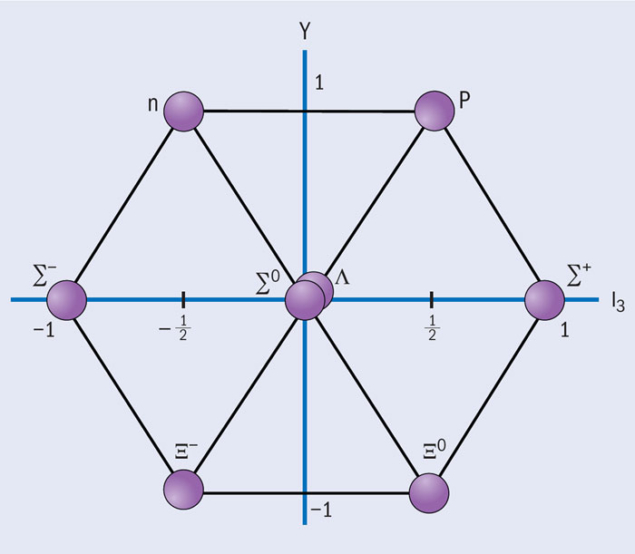
The observed hadrons are members of specific representations of SU(3). The baryons are octets and decuplets, the mesons are octets and singlets. The baryon octet contains the two nucleons, the three Σ hyperons, the Λ hyperon and the two Ξ hyperons (see figure 1). The members of the meson octet are the three pions, the η meson, the two K mesons and the two K mesons.
In 1961, nine baryon resonances were known, including the four Δ resonances. These resonances could not be members of an octet. Gell-Mann and Ne’eman suggested that they should be described by an SU(3)-decuplet but one particle was missing. They predicted that this particle, the Ω–, should soon be discovered with a mass of around 1680 MeV. It was observed in 1964 at the Brookhaven National Laboratory by Nicholas Samios and his group. Thus the baryon resonances were members of an SU(3) decuplet.
It was not clear at the time why the members of the simplest SU(3) representation, the triplet representation, were not observed in experiments. These particles would have non-integral electric charges: 2/3 or –1/3.
The quark model
In 1964, Gell-Mann and Feynman’s PhD student George Zweig, who was working at CERN, proposed that the baryons and mesons are bound states of the hypothetical triplet particles (Gell-Mann 1964, Zweig 1964). Gell-Mann called the triplet particles “quarks”, using a word that had been introduced by James Joyce in his novel Finnegans Wake.
Since the quarks form an SU(3) triplet, there must be three quarks: a u quark (charge 2/3), a d quark (charge –1/3) and an s quark (charge –1/3). The proton is a bound state of two u quarks and one d quark (uud). Inside the neutron are two d quarks and one u quark (ddu). The Λ hyperon has the internal structure uds. The three Σ hyperons contain one s quark and two u or two d quarks (uus or dds). The Ξ hyperons are the bound states uss and dss. The Ω– is a bound state of three s quarks: sss. The eight mesons are bound states of a quark and an antiquark.
In the quark model, the breaking of the SU(3)-symmetry can be arranged by the mass term for the quarks. The mass of the strange quark is larger than the masses of the two non-strange quarks. This explains the mass differences inside the baryon octet, the baryon decuplet and the meson octet.
Introducing colour
In the summer of 1970, I spent some time at the Aspen Center of Physics, where I met Gell-Mann and we started working together. In the autumn we studied the results from SLAC on the deep-inelastic scattering of electrons and atomic nuclei. The cross-sections depend on the mass of the virtual photon and the energy transfer. However, the experiments at SLAC found that the cross-sections at large energies depend only on the ratio of the photon mass and the energy transfer – they showed a scaling behaviour, which had been predicted by James Bjorken.

Image credit: courtesy H Fritzsch.
In the SLAC experiments, the nucleon matrix-element of the commutator of two electromagnetic currents is measured at nearly light-like distances. Gell-Mann and I assumed that this commutator can be abstracted from the free-quark model and we formulated the light-cone algebra of the currents (Fritzsch and Gell-Mann 1971). Using this algebra, we could understand the scaling behaviour. We obtained the same results as Richard Feynman in his parton model, if the partons are identified with the quarks. It later turned out that the results of the light-cone current algebra are nearly correct in the theory of QCD, owing to the asymptotic freedom of the theory.
The Ω– is a bound state of three strange quarks. Since this is the ground state, the space wave-function should be symmetrical. The three spins of the quarks are aligned to give the spin of the omega minus. Thus the wave function of the Ω– does not change if two quarks are interchanged. However, the wave function must be antisymmetric according to the Pauli principle. This was a great problem for the quark model.
In 1964, Oscar Greenberg discussed the possibility that the quarks do not obey the Pauli statistics but rather a “parastatistics of rank three”. In this case, there is no problem with the Pauli statistics but it was unclear whether parastatistics makes any sense in a field theory of the quarks.
Two years later, Moo-Young Han and Yoichiro Nambu considered nine quarks instead of three. The electric charges of these quarks were integral. In this model there were three u quarks: two of them had electric charge of 1, while the third one had charge 0 – so on average the charge was 2/3. The symmetry group was SU(3) × SU(3), which was assumed to be strongly broken. The associated gauge bosons would be massive and would have integral electric charges.
In 1971, Gell-Mann and I found a different solution of the statistics problem (Fritzsch and Gell-Mann 1971). We considered nine quarks, as Han and Nambu had done, but we assumed that the three quarks of the same type had a new conserved quantum number, which we called “colour”. The colour symmetry SU(3) was an exact symmetry. The wave functions of the hadrons were assumed to be singlets of the colour group. The baryon wave-functions are antisymmetric in the colour indices, denoted by red (r), green (g) and blue (b):

Thus the wave function of a baryon changes sign if two quarks are exchanged, as required by the Pauli principle. Likewise, the wave functions of the mesons are colour singlets:

The cross-section for electron–positron annihilation into hadrons at high energies depends on the squares of the electric charges of the quarks and on the number of colours. For three colours this leads to:

Without colours this ratio would be 2/3. The experimental data, however, were in agreement with a ratio of 2.
In 1971–1972, Gell-Mann and I worked at CERN. Together with William Bardeen we investigated the electromagnetic decay of the neutral pion into two photons. It was known that in the quark model the decay rate is about a factor nine less than the measured decay rate – another problem for the quark model.
The decay amplitude is given by a triangle diagram, in which a quark–antiquark pair is created virtually and subsequently annihilates into two photons. We found that after the introduction of colour, the decay amplitude increases by a factor three – each colour contributes to the amplitude with the same strength. For three colours, the result agrees with the experimental value.
(Image credit: From figure 5 in Siegfried Bethke and Peter Zerwas 2004 Physik Journal 3 12 31.)
In the spring of 1972, we started to interpret the colour group as a gauge group. The resulting gauge theory is similar to quantum electrodynamics (QED). The interaction of the quarks is generated by an octet of massless colour gauge bosons, which we called gluons (Fritzsch and Gell-Mann 1972). We later introduced the name “quantum chromodynamics”, or QCD. We published details of this theory one year later together with Heinrich Leutwyler (Fritzsch et al. 1972).
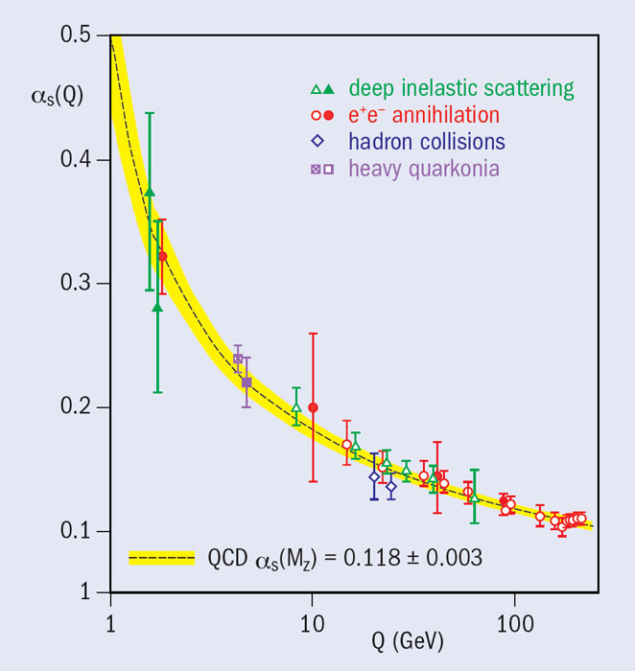
In QCD, the gluons interact not only with the quarks but also with themselves. This direct gluon–gluon interaction is important – it leads to the reduction of the coupling constant at increasing energy, i.e. the theory is asymptotically free, as discovered in 1972 by Gerard ’t Hooft (unpublished) and in 1973 by David Gross, David Politzer and Frank Wilczek. Thus at high energies the quarks and gluons behave almost as free particles. This leads to the approximate “scaling behaviour” of the cross-sections in the deep-inelastic lepton–hadron scattering. The quarks behave almost as free particles at high energies.
The logarithmic decrease of the coupling constant depends on the QCD energy-scale parameter, Λ, which is a free parameter and has to be measured in the experiments. The current experimental value is:

Experiments at SLAC, DESY, CERN’s Large Electron–Positron (LEP) collider and Fermilab’s Tevatron have measured the decrease of the QCD coupling-constant (figure 2). With LEP, it was also possible to determine the QCD coupling-constant at the mass of the Z boson rather precisely:

It is useful to consider the theory of QCD with just one heavy quark Q. The ground-state meson in this hypothetical case would be a quark–antiquark bound state. The effective potential between the quark and its antiquark at small distances would be a Coulomb potential proportional to 1/r, where r is the distance between the quark and the antiquark. However, at large distances the self-interaction of the gluons becomes important. The gluonic field lines at large distances do not spread out as in electrodynamics. Instead, they attract each other. Thus the quark and the antiquark are connected by a string of gluonic field lines (figure 3). The force between the quark and the antiquark is constant, i.e. it does not decrease as in electrodynamics. The quarks are confined. It is still an open question whether this applies also to the light quarks.

In electron–positron annihilation, the virtual photon creates a quark and an antiquark, which move away from each other with high speed. Because of the confinement property, mesons – mostly pions – are created, moving roughly in the same direction. The quark and the antiquark “fragment” to produce two jets of particles. The sum of the energies and momenta of the particles in each jet should be equal to the energy of the original quark, which is equal to the energy of each colliding lepton. These quark jets were observed for the first time in 1978 at DESY (figure 4). They had already been predicted in 1975 by Feynman.
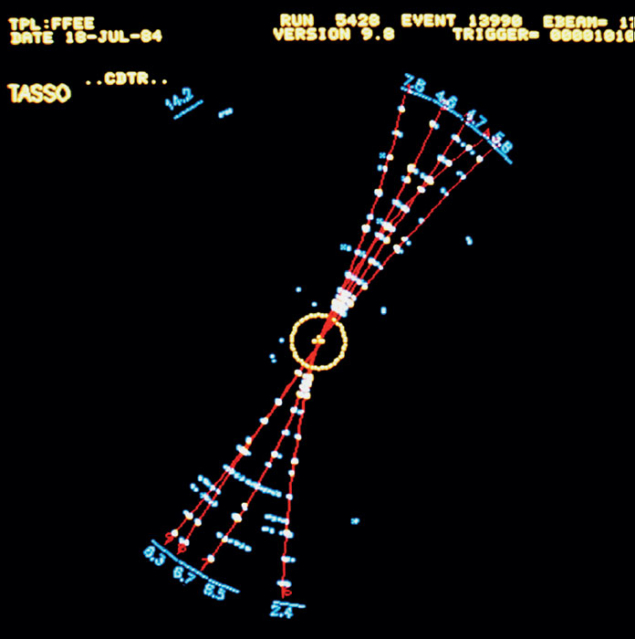
Image credit: Oxford University PPU.
If a quark pair is produced in electron–positron annihilation, then QCD predicts that sometimes a high-energy gluon should be emitted from one of the quarks. The gluon would also fragment and produce a jet. So, sometimes three jets should be produced. Such events were observed at DESY in 1979 (figure 4).
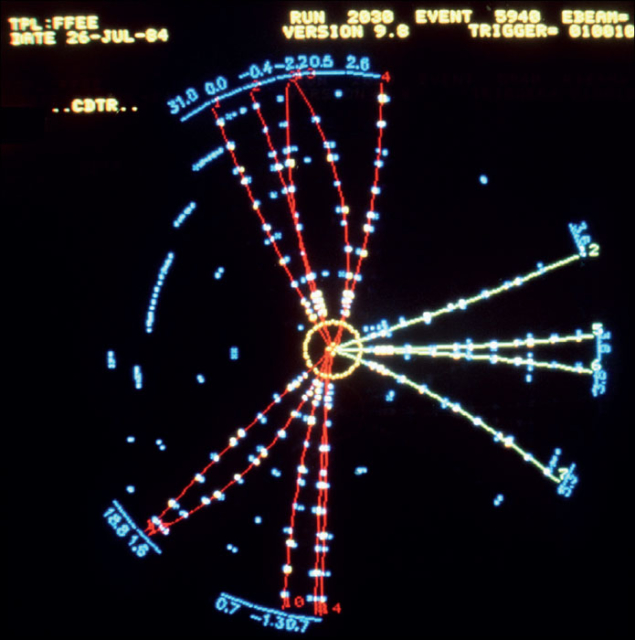
Image credit: Oxford University PPU.
The basic quanta of QCD are the quarks and the gluons. Two colour-octet gluons can form a colour singlet. Such a state would be a neutral gluonium meson. The ground state of the gluonium mesons has a mass of about 1.4 GeV. In QCD with only heavy quarks, this state would be stable but in the real world it would mix with neutral quark–antiquark mesons and would decay quickly into pions. Thus far, gluonium mesons have not been identified clearly in experiments.
The simplest colour-singlet hadrons in QCD are the baryons – consisting of three quarks – and the mesons, made of a quark and an antiquark. However, there are other ways to form a colour singlet. Two quarks can be in an antitriplet – they can form a colour singlet together with two antiquarks. The result would be a meson consisting of two quarks and two antiquarks. Such a meson is called a tetraquark. Three quarks can be in a colour octet, as well as a quark and an antiquark. They can form a colour-singlet hadron, consisting of four quarks and an antiquark. Such a baryon is called a pentaquark. So far, tetraquark mesons and pentaquark baryons have not been clearly observed in experiments.
The three quark flavours were introduced to describe the symmetry given by the flavour group SU(3). However, we now know that in reality there are six quarks: the three light quarks u, d, s and the three heavy quarks c (charm), b (bottom) and t (top). These six quarks form three doublets of the electroweak symmetry group SU(2):

Image credit: Fermilab.
The masses of the quarks are arbitrary parameters in QCD, just as the lepton masses are in QED. Since the quarks do not exist as free particles, their masses cannot be measured directly. They can, however, be estimated using the observed hadron masses. In QCD they depend on the energy scale under consideration. Typical values of the quark masses at the energy of 2 GeV are:
The mass of the t quark is large, similar to the mass of a gold atom. Owing to this large mass, the t quark decays by the weak interaction with a lifetime that is less than the time needed to form a meson. Thus there are no hadrons containing a t quark.
The theory of QCD is the correct field theory of the strong interactions and of the nuclear forces. Both hadrons and atomic nuclei are bound states of quarks, antiquarks and gluons. It is remarkable that a simple gauge theory can describe the complicated phenomena of the strong interactions.





