Supergravity celebrates quarter of a century

The development of supergravity is a landmark in the intertwined histories of gauge field theory and quantum gravity. Culminating the drive towards higher symmetry within quantum field theory, it opens a door to the unification of all forces, and the possibility for extra dimensions. As a candidate theory of everything, supergravity was eclipsed by strings, yet in recent years it has re-emerged as a key component of “modern” string theory, playing an essential role in connecting field theories with string theories, and string theories with each other. Supergravity is as much on theorists’ minds now as it was in the mid-1970s. On 3-4 December 2001, an international meeting, “Supergravity at 25”, was hosted by the C N Yang Institute for Theoretical Physics at the Stony Brook campus of the State University of New York, to commemorate the anniversary of this protean theory, and to assess its ongoing role today.

The modern era of field theory began with the discovery of nonabelian gauge invariance by Chen Ning Yang and Robert L Mills in 1954. A decade and a half later, Gerard ‘t Hooft and Martinus Veltman famously proved that a large class of nonabelian gauge theories can be quantized and renormalized consistently.

Before long, the elements of the Standard Model had fallen into place, and theorists hurried forward toward a “grand” unification of the strong and electroweak interactions.

Charmed circle

Gravity, however, remained outside this charmed quantum circle. The force in quantum gravity is carried by the spin-2 graviton, and could not immediately be unified with Standard Model forces, carried by the spin-1 photon, weak bosons and gluons. The same spin-2 graviton leads to particularly aggressive high-energy behaviour. This results in a hopelessly ambiguous theory, through the proliferation of new infinities at each level of calculation. In technical terms, Einstein’s gravity is not renormalizable. The first inspirations for supergravity were to address these two problems. The novel element was another form of unification, supersymmetry, which relates bosons and fermions. According to this theory, there exists for every boson in nature a fermionic partner, and vice versa. The fermionic partner of the graviton is the gravitino. CERN will search for superpartners of Standard Model particles at the Large Hadron Collider. Within supersymmetry, it was hoped that gravity would be united with other forces, and, through a special combination of particles and interactions, would even turn out to be finite.

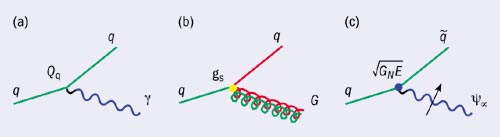
In this context, the progression of field theory from quantum electrodynamics (QED) to supergravity is illustrated in figure 1. The basic interaction of QED is the emission of a photon (g) from a charged particle, like a quark (q), with an amplitude proportional to the quark’s electric charge, (Q_q in figure 1a). We say that the photon is the gauge particle of the electric current. The photon itself, however, is electrically neutral. At the next level of complexity, nonabelian gauge theories like quantum chromodynamics (QCD) introduce an array of “colour” charges, each of which is conserved. In this case, the gluon (G) is the gauge particle of the colour currents, and carries them as well. Thus, when a gluon is emitted (figure 1b), it connects quarks of different colour, with an amplitude proportional to the strong coupling (g_s). All of the colour charges are conserved in the full system of quarks and gluons, and the gluon is represented as a double line to emphasize its colour structure.

In supergravity, currents that describe the flow of energy, momentum and spin combine into a set, called the supercurrent multiplet, analogous to the currents of electric and colour charges in QED and QCD. Part of this multiplet is the energy-momentum tensor, but part is the “supercurrent” itself, a hybrid field with a vector and a spinor index, related to the energy-momentum tensor by a supersymmetry transformation. The spin-2 graviton is the gauge particle of the energy-momentum tensor, while its “superpartner” the spin-3/2 gravitino (y_m) is the gauge particle of the supercurrent. The gravitino is emitted with an amplitude proportional to the energy carried by this current, multiplied by the square root of Newton’s constant (figure 1c). The gravitino (with an extra arrow in the figure to emphasize its spin structure) carries no electric and colour charges, but connects particles with different spin, in this case a quark and scalar supersymmetric partner “squark” (~q). It thus reveals the underlying unity of the quark and squark within their own supermultiplet, in much the same way that the gluon connects quarks that are unified within a multiplet of three colours.

The development of supergravity 25 years ago may be thought of as the exercise of identifying a minimal set of interactions between gravitons and gravitinos that respects general co-ordinate invariance and makes supersymmetry a gauge symmetry. Today this is as routine as writing down the Lagrangian for a Yang-Mills theory. In 1976, however, it was not even clear that it was possible. The task of formulating the minimal supergravity theory was accomplished by Sergio Ferrara, then at the Ecole Normale Supérieure, and Daniel Freedmann and Peter van Nieuwenhuizen of Stony Brook (see further reading list). At the December meeting, they recalled days of alternating hope and despair, which reached a climax one evening in the spring of 1976, when 2000 terms generated by an infinitesimal supersymmetry transformation were miraculously cancelled by computer. With this result, supergravity moved from conjecture to consistency. Their approach, which they called the “Noether method”, was based on building the correct transformation laws by retracing the reasoning of Emmy Noether’s famous theorem connecting symmetries and conservation laws. Shortly afterwards, Stanley Deser of Brandeis University and Bruno Zumino of CERN gave a useful reformulation (see further reading list), and in the early months and years of supergravity, other approaches gave further insights and dramatic simplifications. A systematization of what quickly became a veritable zoo of supergravity theories was provided by the superspace approach of Julius Wess and Zumino, developed by S James Gates, Jr and Warren Siegel, and the tensor calculus developed by Ferrara and van Nieuwenhuizen, and independently by Kellogg S Stelle of Imperial College, London, and Peter West of King’s College, London.

Supergravity today

Participants at the symposium included the original authors, along with others, such as Marc Grisaru of Brandeis University, who recalled classic investigations into the new theory. Many presentations, however, addressed the role of supergravity today. It fell to string theory to provide a finite quantum theory of gravity, matter and other forces. Our grasp of string theory is incomplete, however, because we lack an understanding of its ground (vacuum) state, and in the larger sense, its non-perturbative spectrum of states. This is one area where supergravity is central to the study of string theory. At the meeting, aspects of the dualities between different string theories were discussed by Bernard Julia of the Ecole Normale Supérieure, Igor Klebanov of Princeton, and West. These dualities have led to a compelling conjecture that all the consistent (10-dimensional) string theories are actually different vacua of a single underlying theory, M-theory, whose low-energy limit is 11-dimensional supergravity. Properties of 11-dimensional supergravity do indeed shed light on string theories in 10 dimensions. In addition, many special solutions to the supergravity equations of motion can be identified with objects in string theory called D-branes, a theme discussed at the conference by Gary Gibbons of Cambridge University, Pietro Fré of Turin, and Kostas Skenderis of Princeton. D-branes are central to a program described by Ashoke Sen of India’s Harish-Chandra Research Institute, for a closed-string theory based on open strings, and aspects of D-brane dynamics were discussed by Michigan’s Michael Duff, Stockholm’s Ulf Lindström, and John Schwarz of Caltech. Bernard de Wit of Utrecht and Ferrara discussed recent developments in supergravities with more than one supersymmetry.

Supergravity is also central to a remarkable discovery called the AdS/CFT correspondence, which relates supergravity in higher-dimensional anti-de Sitter (AdS) space-time (a space-time with constantly negative curvature) to strongly coupled gauge field theories (CFT). This correspondence, which relates quantum correlations in the field theory to classical solutions of supergravity, was discussed by Freedman, Klebanov, Emery Sokatchev from CERN, Ergin Sezgin from Texas A&M, Arkady Tseytlin from Ohio State and Nicholas Warner from the University of Southern California (USC). Supergravity’s possible role in cosmology was discussed by Renata Kallosh of Stanford.

In part, the meeting celebrated the influence of supergravity (thousands of papers have the word in their title, and thousands more list it as a keyword). Even more impressively, it demonstrated its vitality. Though supergravity is 25 years old, the conference had the excitement and energy characteristic of a recent discovery. Only half in jest, some participants looked forward to new and unexpected developments to be celebrated on supergravity’s 50th birthday.