NNLO calculations keep pace with precision of LHC experiments.

Image credit: Daniel Dominguez, CERN.
Studying matter at the highest energies possible has transformed our understanding of the microscopic world. CERN’s Large Hadron Collider (LHC), which generates proton collisions at the highest energy ever produced in a laboratory (13 TeV), provides a controlled environment in which to search for new phenomena and to address fundamental questions about the nature of the interactions between elementary particles. Specifically, the LHC’s main detectors – ATLAS, CMS, LHCb and ALICE – allow us to measure the cross-sections of elementary processes with remarkable precision. A great challenge for theorists is to match the experimental precision with accurate theoretical predictions. This is necessary to establish the Higgs sector of the Standard Model of particle physics and to look for deviations that could signal the existence of new particles or forces. Pushing our current capabilities further is key to the success of the LHC physics programme.
Underpinning the prediction of LHC observables at the highest levels of precision are perturbative computations of cross-sections. Perturbative calculations have been carried out since the early days of quantum electrodynamics (QED) in the 1940s. Here, the smallness of the QED coupling constant is exploited to allow the expressions for physical quantities to be expanded in terms of the coupling constant – giving rise to a series of terms with decreasing magnitude. The first example of such a calculation was the one-loop QED correction to the magnetic moment of the electron, which was carried out by Schwinger in 1948. It demonstrated for the first time that QED was in agreement with the experimental discovery of the anomalous magnetic moment of the electron, ge-2 (the latter quantity was dubbed “anomalous” precisely because, prior to Schwinger’s calculation, it did not agree with predictions from Dirac’s theory). In 1957, Sommerfeld and Petermann computed the two-loop correction, and it took another 40 years until, in 1996, Laporta and Remiddi computed analytically the three-loop corrections to ge-2 and, 10 years later, even the four- and five-loop corrections were computed numerically by Kinoshita et al. The calculation of QED corrections is supplemented with predictions for electroweak and hadronic effects, and makes ge-2 one of the best known quantities today. Since ge-2 is also measured with remarkable precision, it provides the best determination of the fine-structure constant with an error of about 0.25 ppb. This determination agrees with other determinations, which reach an accuracy of 0.66 ppb, showcasing the remarkable success of quantum field theory in describing material reality.
In the case of proton–proton collisions at the LHC, the dominant processes involve quantum chromodynamics (QCD). Although in general the calculations are more complex than in QED due to the non-abelian nature of this interaction, i.e. the self-coupling of gluons, the fact that the QCD coupling constant is small at the high energies relevant to the LHC means that perturbative methods are possible. In practice, all of the Feynman diagrams that correspond to the lowest-order process are drawn by considering all possible ways in which a given final state can be produced. For instance, in the case of Drell–Yan production at the LHC, the only lowest-order diagram involves an incoming quark and an incoming antiquark from the proton beams, which annihilate to produce a Z, γ* or a W boson, which then decays into leptons. Using the Feynman rules, such pictorial descriptions can be turned into quantum-mechanical amplitudes. The cross-section can then be computed as the square of the amplitude, integrated over the phase space and appropriately summing and averaging over quantum numbers.

Image credit: Camb. Monogr. Part. Phys. Nucl. Phys. Cosmol. 81 1.
This lowest-order description is very crude, however, since it does not account for the fact that quarks tend to radiate gluons. To incorporate such higher-order quantum corrections, next-to-leading order (NLO) calculations that describe the radiation of one additional gluon are required. This gluon can either be real, giving rise to a particle that is recorded by a detector, or virtual, corresponding to a quantum-mechanical fluctuation that is emitted and reabsorbed. Both contributions are divergent because they become infinite in the limit when the energy of the gluon is infinitesimally small, or when the gluon is exactly collinear to one of the emitting quarks. When real and virtual corrections are combined, however, these divergences cancel out. This is a consequence of the so-called Kinoshita–Lee–Nauenberg theorem, which states that low-energy (infrared) divergences must cancel in physical (measurable) quantities.
Even if divergences cancel in the final result, a procedure to handle divergences in intermediate steps of the calculations is still needed. How to do this at the level of NLO corrections has been well understood for a number of years. The first successes of NLO QCD calculations came in the 1990s with the comparison of Drell–Yan particle-production data recorded by CERN’s SPS and Fermilab’s Tevatron experiments to leading-order and NLO QCD predictions, which had first been computed in 1979 by Altarelli, Ellis and Martinelli. The comparison revealed unequivocally that NLO corrections are required to describe Drell–Yan data, and marked the first great success of perturbative QCD (figure 1).
Things have changed a lot since then. Today, NLO corrections have been calculated for a large class of processes relevant to the LHC programme, and several tools have been developed to even compute them in a fully automated way. As a result, the problem of NLO QCD calculations is considered solved and comparing these to data has become standard in current LHC data analysis. Thanks to the impressive precision now being attained by the LHC experiments, however, we are now being taken into the complex realm of higher-order calculations.
The NNLO explosion
The new frontier in perturbative QCD is the calculation of next-to-next-to-leading order (NNLO) corrections. At the level of diagrams, the picture is once again pretty simple: at NNLO level, it is not just one extra particle emission but two extra emissions that are accounted for. These emissions can be two real partons (quarks or gluons), a real parton and a virtual one, or two virtual partons.
The first NNLO computation for a collider process concerned “inclusive” Drell–Yan production, by Hamberg, Van Neerven and Matsuura in 1991. Motivated by the SPS and Tevatron data, and also by the planned LHC and SSC experiments, this was a pioneering calculation that was performed analytically. The second NNLO calculation, in 2002, was for inclusive Higgs production in gluon–gluon fusion by Harlander and Kilgore. Inclusive calculations refer only to the total cross-section for producing a Higgs boson or a Drell–Yan pair without any restriction on where these particles end up, which is not measurable because detectors do not cover the entire phase space such as the region close to the beam.
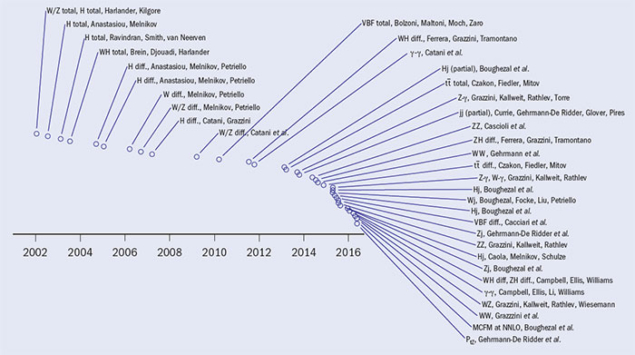
Image credit: From the talk given by G P Salam at the 2016 LHCP conference.
The first “exclusive” NNLO calculations, which allow kinematic cuts to be applied to the final state, started to appear in 2004 for Drell–Yan and Higgs production. These calculations were motivated by the need to predict quantities that can be directly measured, rather then relying on extrapolations to describe the effects of experimental cuts. The years 2004–2011 saw more activity, but limited progress: all calculations were essentially limited to “2 → 1” scattering processes, in essence Higgs and Drell–Yan production, as well as Higgs production in association with a Drell–Yan pair. From a QCD point of view, the latter process is simply off-shell Drell–Yan production in which the vector boson radiates a Higgs. A few 2 → 2 calculations started to appear in 2012, most notably top-pair production and the production of a pair of vector bosons. It is only in the past two years, however, that we have witnessed an explosion of NNLO calculations (figure 2). Today, all 2 → 2 Standard Model LHC scattering processes are known to NNLO, thanks to remarkable progress in the calculation of two-loop integrals and in the development of procedures to handle intermediate divergences.
Compared to NLO calculations, NNLO calculations are substantially more complex. Two main difficulties must be faced: loop integrals and divergences. Two-loop integrals have been calculated in the past by explicitly performing the multi-dimensional integration, in which each loop gives rise to a “D-dimensional” integration. For simple cases, analytical expressions can be found, but in many cases only numerical results can be obtained for these integrals. The complexity increases with the number of dimensions (i.e. the number of loops) and with the number of Lorentz-invariant scales involved in the process (i.e. the number of particles involved, and in particular the number of massive particles).
Recently, new approaches to these loop integrals have been suggested. In particular, it has been known since the late 1990s that integrals can be treated as variables entering a set of differential equations, but solutions to those equations remained complicated and could be found only on a case-by-case basis. A revolution came about just three years ago when it was realised that the differential equations can be organised in a simple form that makes finding solutions, i.e. finding expressions for the wanted two-loop integrals, a manageable problem. Practically, the set of multi-loop integrals to be computed can be regarded as a set of vectors. Decomposing these vectors in a convenient set of basis vectors can lead to significant simplifications of the differential equations, and concrete criteria were proposed for finding an optimal basis. The very important NNLO calculations of diboson production have benefitted from this technology.
Currently, when only virtual massless particles are involved and up to a total of four external particles are considered, the two-loop integral problem is considered solved, or at least solvable. However, when massive particles circulate in the loop, as is the case for a number of LHC processes, the integrals give rise to a new class of functions, elliptic functions, and it is not yet understood how to solve the associated differential equations. Hence, for processes with internal masses we still face a conceptual bottleneck. Overcoming this will be very important for Higgs studies at large transverse momentum, where the top loop to which the Higgs couples is resolved. The calculation of these integrals is today an area with tight connections to more formal and mathematical areas, leading to close collaborations between the high-energy physics and the mathematical/formal-oriented communities.
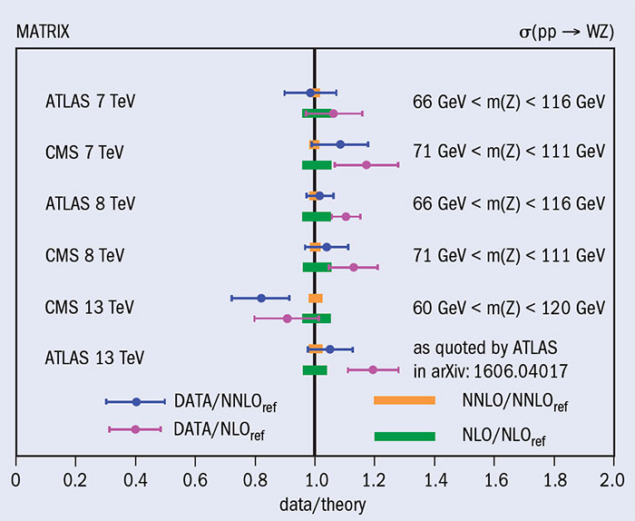
Image credit: Phys. Lett. B 761 179.
The second main difficulty in NNLO calculations is that, as at NLO, individual contributions are divergent in the infrared region, i.e. when particles have a very small momentum or become collinear with respect to one another, and the structure of these singularities is now considerably more complex because of the extra particle radiated at NNLO. All singularities cancel when all contributions are combined, but to have exclusive predictions it is necessary to cancel the singularities before performing integrations over the phase space. Compared to NLO, where systematic ways to treat these intermediate divergences have been known for many years, the problem is more difficult at NNLO because there are more divergent configurations and different divergences overlap. The past few years have seen remarkable developments in the understanding and treatment of infrared singularities in NNLO computations of cross-sections, and a range of methods based on different physical ideas have been successfully applied.
Beyond NNLO
Is the field of precision calculations close to coming to an end? The answer is, of course, no. First, while the problem of cancelling singularities is in principle solved in a generic way, in practice all methods have been applied to 2 → 2 processes only, and no 2 → 3 cross-section calculation is foreseen in the near future. For instance, the very important processes of three-jet production or Higgs production in association with a top-quark pair are known to NLO accuracy only. Similarly, two-loop pentagon integrals required for the calculation of 2 → 3 scatterings are at the frontier of what can be done today. Furthermore, most of the existing NNLO computer codes require extremely long runs on large computer farms, with typical run times of several CPU years. It could be argued that this is not an issue in an age of large computer farms and parallel processing and when CPU time is expected to become cheaper over the years, however, the number of phenomenological studies that can be done with a theory prediction is much larger when calculations can be performed quickly on a single machine. Hence, in the coming years NNLO calculations will be scrutinised and compared in terms of their performances. Ultimately, only one or a few of the many existing methods to perform integrals and to treat intermediate divergences is likely to take over.
Given how hard and time-consuming NNLO calculations are, we should also ask if it is worth the effort. A comparison with data for the diboson (WZ) production process at different LHC beam energies to NLO and NNLO calculations (figure 3) provides an indication of the answer. It is clear that LHC data already indicate a clear preference for NNLO QCD predictions and that, once more data are accumulated, NLO will likely be insufficient. While it is early days for NNLO phenomenology, the same conclusion applies to other measurements examined so far.
In the past, accurate precision measurements have provided a strong motivation to push the precision of theoretical predictions. On the other side, very precise theory predictions have stimulated even more precise measurements. Today, the accuracy reached by LHC measurements is by far better than what anybody could have predicted when the LHC was designed. For instance, the Z transverse momentum spectrum reaches an accuracy of better than a per cent over a large range of transverse momentum values, which will be important to further constrain parton-distribution functions, and the mass of the W boson, which enters precision tests of the Standard Model, is measured with better than 20 MeV accuracy. In the future, one should expect that high-precision theoretical predictions will push the experimental precision beyond today’s foreseeable boundaries. This will usher in the next phase in perturbative QCD calculations: next-to-next-to-next-to-leading order, or N3LO.
Today we have two pioneering calculations beyond NNLO: the N3LO calculation of inclusive Higgs production (in the large top-mass approximation), and the N3LO calculation of inclusive vector-boson-fusion Higgs production. Both calculations are inclusive over radiation, exactly in the same way that the first NNLO calculations were. These calculations are now suggestive of a good convergence of the perturbative expansion, meaning that the N3LO correction is very small and that the N3LO result lies well within the theoretical uncertainty band of the NNLO result. Turning these calculations into fully exclusive predictions is the next theoretical challenge.








