The Cabibbo angle, 60 years later

In a 1961 book, Richard Feynman describes the great satisfaction he and Murray Gell-Mann felt in formulating a theory that explained the close equality of the Fermi constants for muon and neutron-beta decay. These two physicists and, independently, Gershtein and Zeldovich, had discovered the universality of weak interactions. It was a generalisation of the universality of electric charge and strongly suggested the existence of a common origin of the two interactions, an insight that was the basis for unified theories developed later. 

Fermi’s description of neutron beta decay (n → p + e^– + ν_e) involved the product of two vector currents analogous to the electromagnetic current: a nuclear current transforming the neutron into a proton and a leptonic current creating the electron–antineutrino pair. Subsequent studies of nuclear decays and the discovery of parity violation complicated the description, introducing all possible kinds of relativistically invariant interactions that could be responsible for neutron beta decay. 

The decay of the muon (μ^– → ν_μ + e^– + ν_e) was also found to involve the product of two vector currents, one transforming the muon into its own neutrino and the other creating the electron–antineutrino pair. What Feynman and Gell-Mann, and Gershtein and Zeldovich, had found is that the nuclear and lepton vector currents have the same strength, despite the fact that the n → p transition is affected by the strong nuclear interaction while μ → ν_μ and e → ν_e transitions are not (we are anticipating here what was discovered only later, namely that the electron and muon each have their own neutrino). 

At the end of the 1950s, simplicity finally emerged. As proposed by Sudarshan and Marshak, and by Feynman and Gell-Mann, all known beta decays are described by the products of two currents, each a combination of a vector and an axial vector current. Feynman notes: after 23 years, we are back to Fermi! 

The book of 1961, however, also records Feynman’s dismay after the discovery that the Fermi constants of strange-particle beta decays, for example the lambda–hyperon beta decay: Λ → p+ e^– + ν_e were smaller by a factor of four or five than the theoretical prediction. In 1960 Gell-Mann, together with Maurice Lévy, had tried to solve the problem but, while taking a step in the right direction, they concluded that it was not possible to make quantitative predictions for the observed decays of the hyperons. It was up to Nicola Cabibbo, in a short article published in 1963 in Physical Review Letters, to reconcile strange-particle decays with the universality of weak interactions, paving the way to the modern unification of electromagnetic and weak interactions. 

Over to Frascati 

Nicola had graduated in Rome in 1958, under his tutor Bruno Touschek. Hired by Giorgio Salvini, he was the first theoretical physicist in the Electro-Synchrotron Frascati laboratories. There, Nicola met Raoul Gatto, five years his elder, who was coming back from Berkeley, and they began an extremely fruitful collaboration. 

These were exciting times in Frascati: the first e⁺ e^– collider, AdA (Anello di Accumulazione), was being realised, to be followed later by a larger machine, Adone, reaching up to 3 GeV in the centre of mass. New particles were studied at the electro-synchrotron, related to the newly discovered SU(3) flavour symmetry (e.g. the η meson). Cabibbo and Gatto authored an important article on e⁺ e^– physics and, in 1961, they investigated the weak interactions of hadrons in the framework of the SU(3) symmetry. Gatto and Cabibbo and, at the same time, Coleman and Glashow, observed that vector currents associated with the SU(3) symmetry by Noether’s theorem include a strangeness-changing current, V(ΔS = 1), that could be associated with strangeness-changing beta-decays in addition to the isospin current, V(ΔS = 0), responsible for strangeness-non-changing beta decays – the same considered by Feynman and Gell-Mann. For strange-particle decays, the identification implied that the variation of strangeness in the hadronic system has to be equal to the variation of the electric charge (in short: ΔS = ΔQ). The rule is satisfied in Λ beta decay (Λ: S = –1, Q = 0; p: S = 0, Q = +1). However, it conflicted with a single event allegedly observed at Berkeley in 1962 and interpreted as Σ⁺ → n + μ⁺ + ν_μ, which had ΔS = –ΔQ (Σ⁺: S = –1, Q = +1; n: S = Q = 0). In addition, the problem remained of how to correctly formulate the concept of muon-hadron universality in the presence of four vector currents describing the transitions e → ν_e, μ → ν_μ, n → p and Λ → p.

Cabibbo’s angle

In his 1963 paper, written while he was working at CERN, Nicola made a few decisive steps. First, he decided to ignore the evidence of a ΔS = –ΔQ component suggested by Berkeley’s Σ⁺ → n + μ⁺ + ν_μ event. Nicola was a good friend of Paolo Franzini, then at Columbia University, and the fact that Paolo, with larger statistics, had not yet seen any such event provided a crucial hint. Next, to describe both ΔS = 0 and ΔS = 1 weak decays, Nicola formulated a notion of universality between each leptonic vector current (electronic or muonic) and one, and only one, hadronic vector current. He assumed the current to be a combination of the two currents determined by the SU(3) symmetry that he had studied with Gatto in Frascati (also identified by Coleman and Glashow): V_hadron = aV(ΔS = 0) + bV(ΔS = 1), with a and b being numerical constants. By construction, V(ΔS = 0) and V(ΔS = 1) have the same strength of the electron or of the muon currents; for the hadronic current to have the same strength, one requires a² + b² = 1, that is a = cosθ, b = sinθ. 

Cabibbo obtained the final expression of the hadronic weak current, adding to these hypotheses the V–A formulation of the weak interactions. The angle θ became a new constant of nature, known since then as the Cabibbo angle. 

An important point is that the Cabibbo theory is based on the currents associated with SU(3) symmetry. For one, this means that it can be applied to the beta decays of all hadrons, mesons and baryons belonging to the different SU(3) multiplets. This was not the case for the precursory Gell-Mann–Lévy theory, which also assumed one hadron weak current but was formulated in terms of protons and lambdas, and could not be applied to the other hyperons or to the mesons. In addition, in the limit of exact SU(3) symmetry one can prove a non-renormalisation theorem for the ΔS = 1 vector current, which is entirely analogous to the one proved by Feynman and Gell-Mann for the ΔS = 0 isospin current. The Cabibbo combination, then, guarantees the universality of the full hadron weak current to the lepton current for any value of the Cabibbo angle, the suppression of the beta decays of strange particles being naturally explained by a small value of θ. Remarkably, a theorem derived by Ademollo and Gatto, and by Fubini a few years later, states that the non-renormalisation of the vector current’s strength is also valid to the first order in SU(3) symmetry breaking. 

Photons and quarks

In many instances, Nicola mentioned that a source of inspiration for his assumption for the hadron current was the passage of photons through a polarimeter, a subject he had considered in Frascati in connection with possible experiments of electron scattering through polarised crystals. Linearly polarised photons can be described via two orthogonal states, but what is transmitted is only the linear combination corresponding to the direction determined by the polarimeter. Similarly, there are two orthogonal hadron currents, V (ΔS = 0) and V (ΔS = 1), but only the Cabibbo combination couples to the weak interactions. 

An interpretation closer to particle physics came with the discovery of quarks. In quark language, V(ΔS = 0) induces the transition d → u and V(ΔS = 1) the transition s → u. The Cabibbo combination corresponds then to d_C = (cos θd + sin θs) → u. Stated differently, the u quark is coupled by the weak interaction only to one, specific, superposition of d and s quarks: the Cabibbo combination d_C. This is Cabibbo mixing, reflecting the fact that in SU(3) there are two quarks with the same charge –1/3. 

A first comparison between theory and meson and hyperon beta-decay data was done by Cabibbo in his original paper, in the exact SU(3) limit. Specifically, the value of θ was obtained by comparing K⁺ and π⁺ semileptonic decays. In baryon semileptonic decays, the matrix elements of vector currents are determined by the SU(3) symmetry, while axial currents depend upon two parameters, the so-called F and D couplings. Many fits have been performed in successive years, which saw a dramatic increase in the decay modes observed, in statistics, and in precision. 

Four decades after the 1963 paper, Cabibbo, with Earl Swallow and Roland Winston, performed a complete analysis of hyperon decays in the Cabibbo theory, then embedded in the three-generation Kobayashi and Maskawa theory, taking into account the momentum dependence of vector currents. In their words (and in modern notation):
“… we obtain V_us = 0.2250(27) (= sin θ). This value is of similar precision, but higher than the one derived from Kl3, and in better agreement with the unitarity requirement,
|V_ud |² + |V_us|² + |V_ub |² = 1. We find that the Cabibbo model gives an excellent fit of the existing form factor data on baryon beta decays (χ² = 2.96) for three degrees of freedom with F + D = 1.2670 ± 0.0030, F–D = –0.341±0.016, and no indication of flavour SU(3) breaking effects.” 

The Cabibbo theory predicts a reduction in the nuclear Fermi constant squared with respect to the muonic one by a factor cos² θ = 0.97. The discrepancy had been noticed by Feynman and S Berman, one of Feynman’s students, who estimated the possible effect of electromagnetic radiative corrections. The situation is much clearer today, with precise data coming from super-allowed Fermi nuclear transitions and radiative corrections under control.  

Closing up

From its very publication, the Cabibbo theory was seen as a crucial development. It indicated the correct way to embody lepton-hadron universality and it enjoyed a heartening phenomenological success, which in turn indicated that we could be on the right track for a fundamental theory of weak interactions. 

The idea of quark mixing had profound consequences. It prompted the solution of the spectacular suppression of strangeness-changing neutral processes by the GIM mechanism (Glashow, Iliopoulos and Maiani), where the charm quark couples to the combination of down and strange quarks orthogonal to the Cabibbo combination. Building on Cabibbo mixing and GIM, it has been possible to extend to hadrons the unified SU(2)_L ⊗ U(1) theory formulated, for leptons, by Glashow, and by Weinberg and Salam. 

There are very few articles in the scientific literature in which one does not feel the need to change a single word and Cabibbo’s is definitely one of them

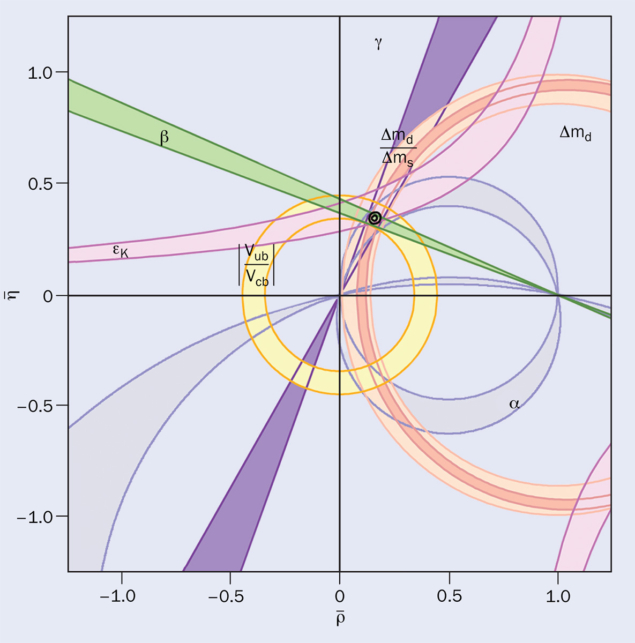
CP symmetry violations observed experimentally had no place in the two-generation scheme (four quarks, four leptons) but found an elegant description by Makoto Kobayashi and Toshihide Maskawa in the extension to three generations. Quark mixing introduced by Cabibbo is now described by a three-by-three unitary matrix known in the literature as the Cabibbo–Kobayashi–Maskawa (CKM) matrix. In the past 50 years the CKM scheme has been confirmed with ever increasing accuracy by a plethora of measurements and impressive theoretical predictions (see “Testing quark mixing” figure). Major achievements have been obtained in the studies of charm- and beauty-particle decays and mixing. The CKM paradigm remains a great success in predicting weak processes and in our understanding of the sources of CP violation in our universe. 

Nicola Cabibbo passed away in 2010. The authoritative book by Abraham Pais, in its chronology, cites the Cabibbo theory among the most important developments in post-war particle physics. In the History of CERN, Jean Iliopoulos writes: “There are very few articles in the scientific literature in which one does not feel the need to change a single word and Cabibbo’s is definitely one of them. With this work, he established himself as one of the leading theorists in the domain of weak interactions.”