Hunting the muon’s forbidden decay

Searching for the decay μ⁺→ e⁺γ is like looking for a needle in a haystack the size of the Great Pyramid of Giza. This simile-stretching endeavour is the task of the MEG II experiment at the Paul Scherrer Institute (PSI) in Villigen, Switzerland. MEG II is an upgrade of the previous MEG experiment, which operated from 2008 to 2013. All experimental data so far are consistent with muon decays that conserve lepton flavour by the production of two appropriately flavoured neutrinos. Were MEG II to observe the neutrinoless decay of the muon to a positron and a photon, it would be the first evidence of flavour violation with charged leptons, and unambiguous evidence for new physics.

Lepton-flavour conservation is a mainstay of every introductory particle-physics course, yet it is merely a so-called accidental symmetry of the Standard Model (SM). Unlike gauge symmetries, it arises because only massless left-handed neutrinos are included in the model. The corresponding mass and interaction terms of the Lagrangian can therefore be simultaneously diagonalised, which means that interactions always conserve lepton flavour. This is not the case in the quark sector, and as a result quark flavour is not conserved in weak interactions. Since lepton flavour is not considered to be a fundamental symmetry, most extensions of the SM predict its violation at a level that could be observed by state-of-the-art experiments.

Indeed an extension of the SM is already required to include the tiny neutrino masses that we infer from neutrino oscillations. In this extension, neutrino oscillations induce charged lepton-flavour-violating processes but with the branching ratio for μ⁺→ e⁺γ emerging to be only 10^–54, which cannot be accessed experimentally (see “Charged lepton-flavour violation in the SM” box). A data sample of muons as large as the number of protons in the Earth would not be enough to see such an improbable decay. Charged lepton-flavour violation is therefore a clear signature of new physics with no SM backgrounds.

Finding the needle

The search requires an intense source of muons, and detectors capable of reconstructing the kinematics of the muon’s decay products with high precision. PSI offers the world’s most intense continuous muon beams, delivering up to 10⁸ muons per second. MEG II (previously as MEG) is designed to search for μ⁺→ e⁺γ by stopping positive muons on a thin target, and looking for positron–photon pairs from muon decays at rest. This method exploits the two-body kinematics of the decay to discriminate signal events from the backgrounds, which are predominantly the radiative muon decay μ⁺→ e⁺ν_e ν̅_μ γ and the accidental time coincidence of a positron and photon produced by different muon decays.

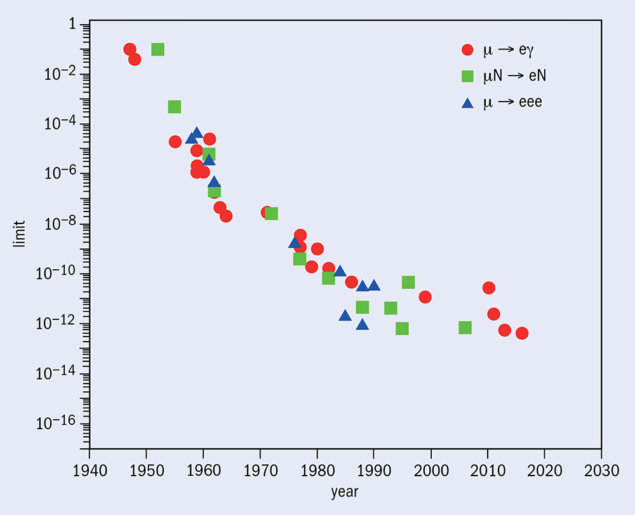
In the late 1990s, when the first MEG experiment was being designed, theorists argued that the μ⁺→ e⁺γ branching ratio could be as high as 10^–12 to 10^–14, based on supersymmetry arising at the TeV scale. Twenty years later, MEG has excluded branching ratios above 4.2 × 10^–13 (figure 1), and supersymmetric particles remain undiscovered at the LHC. Nevertheless, since charged lepton-flavour-violating processes are sensitive to the virtual exchange of new particles, while not requiring their creation as at the LHC, they can probe new physics models (supersymmetry, extra dimensions, leptoquarks, multi-Higgs, etc) up to mass scales of thousands of TeV. Scales such as these are not only unreachable at the LHC, but also at near-future accelerators.

The MEG collaboration therefore decided to upgrade the detectors with the goal of improving the sensitivity of the experiment by a factor of 10. The new experiment, which adopts the same measurement principle, is expected to start taking data at the end of 2019 (figure 2). Photons are reconstructed by a liquid xenon (LXe) detector technology that was pioneered by the MEG collaboration, achieving an unprecedented ~2% calorimetric resolution at energies as low as 52.8 MeV – the energy of the photon in a μ⁺→ e⁺γ decay. The LXe detector provides a high-resolution measurement of the position and timing of the photon conversion, precise to a few millimetres and approximately 70 ps. The positrons are reconstructed in a magnetic spectrometer instrumented with drift chambers for tracking, and scintillator bars for timing. A peculiarity of the MEG spectrometer is a non-uniform magnetic field, diminishing from 1.2 T at the centre of the detector to 0.5 T at the extremities. The gradated field prevents positrons from curling too many times. This avoids pileup in the detectors and makes positrons of the same momentum curl with the same radius, independent of their emission angle, thus simplifying the design and operation of the tracking system.

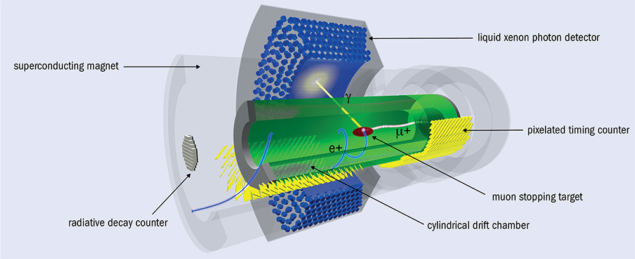
Following a major overhaul that was begun in 2011, all the detectors have now been upgraded. Silicon photomultipliers custom-modified for sensitivity to the ultraviolet LXe scintillation light have replaced conventional photomultipliers on the inner face of the calorimeter. Small scintillating tiles have replaced the scintillating bars of the positron-timing detector to improve timing and reduce pileup. The main challenge when upgrading the drift chambers was dealing with high positron rates. Here, the need for high granularity had to be balanced by keeping the total amount of material low. This reduces both multiple scattering and the rate of positrons annihilating in the material, and contributions to the coincident-photon background in the calorimeter. The solution was the use of extremely thin 40 and 50 μm silver-plated aluminium wires, 20 μm gold-plated tungsten wires, and innovative assembly techniques. All the detectors’ resolutions were improved by a factor of around two with respect to the MEG experiment. The MEG II design also includes a new detector to veto photons coming from radiative muon decays, improved calibration tools and new trigger and data-acquisition electronics to cope with the increased number of readout channels. The improved detector performance will allow the muon beam rate to be more than doubled, from 3.3 × 10⁷ to 7 × 10⁷ muons per second.

The detectors were installed and tested in the muon beam in 2018. In 2019 a test of the whole detector will be completed, with the possibility of collecting the first physics data. The experiment is then expected to run for three years to uncover evidence for the μ⁺→ e⁺γ decay if the branching ratio is around 10^–13 or set a limit of 6 × 10^–14 on its branching ratio.

New directions

In the meantime, PSI researchers are investigating the possibility of building new beamlines with 10⁹ or even 10¹⁰ muons per second to allow experimenters to probe even smaller branching ratios. How could a future experiment cope with such high rates? Preliminary studies are investigating a system where photons are converted into pairs of electrons and positrons, and reconstructed in a tracking device. This solution, which has already been exploited previously by the MEGA experiment at Los Alamos National Laboratory, could also improve the photon resolution.

At the same time, other experiments are searching for charged lepton-flavour violation in other channels. Mu3e, also at PSI, will search for μ⁺→ e⁺e⁺e^– decays. The Mu2e and COMET experiments, at Fermilab and J-PARC, respectively, will search for muon-to-electron conversion in the field of a nucleus. These processes are complementary to μ⁺→ e⁺γ, allowing alternative scenarios to be probed. At the same time, collider experiments such as Belle II and LHCb are working on studies of lepton-flavour violation in tau decays. LHCb researchers are also testing lepton universality, which holds that the weak couplings are the same for each lepton flavour (see The flavour of new physics). As theorists often stress, all these analyses are strongly complementary both with each other and with direct searches for new particles at the LHC.

Ever since the pioneering work of Conversi, Pancini and Piccioni, muons have played a crucial role in the development of particle physics. When I I Rabi exclaimed “who ordered that?”, he surely did not imagine that 80 years later the lightest unstable elementary particle would still be a focus of cutting-edge research.