The neutrino mass puzzle

After all these years, neutrinos remain extraordinary – and somewhat deceptive. The experimental success of the three-massive-neutrino paradigm over the past 25 years makes it easy to forget that massive neutrinos are not part of the Standard Model (SM) of particle physics.

The problem lies with how neutrinos acquire mass. Nonzero neutrino masses are not possible without the existence of new fundamental fields, beyond those that are part of the SM. And we know virtually nothing about the particles associated with them. They could be bosons or fermions, light or heavy, charged or neutral, and experimentally accessible or hopelessly out of reach.

This is the neutrino mass puzzle. At its heart is the particle’s uniquely elusive nature, which is both the source of the problem and the main challenge in resolving it.

Mysterious and elusive

Despite outnumbering other known massive particles in the universe by 10 orders of magnitude, neutrinos are the least understood of the matter particles. Unlike electrons, they do not participate in electromagnetic interactions. Unlike quarks, they do not participate in the strong interactions that bind protons and neutrons together. Neutrinos participate only in aptly named weak interactions. Out of the trillions of neutrinos that the Sun beams through you each second, only a handful will interact with your body during your lifetime.

Neutrino physics has therefore had a rather tortuous and slow history. The existence of neutrinos was postulated in 1930 but only confirmed in the 1950s. The hypothesis that there are different types of neutrinos was first raised in the 1940s but only confirmed in the 1960s. And the third neutrino type, postulated when the tau lepton was discovered in the 1970s, was only directly observed in the year 2000. Nonetheless, over the years neutrino experiments have played a decisive role in the development of the most successful theory in modern physics: the SM. And at the turn of the 21st century, neutrino experiments revealed that there is something missing in its description of particle physics.

Neutrinos are fermions with spin one-half that interact with the charged leptons (the electron, muon and tau lepton) and the particles that mediate the weak interactions (the W and Z bosons). There are three neutrino types, or flavours: electron-type (ν_e), muon-type (ν_μ) and tau-type (ν_τ), and each interacts exclusively with its namesake charged lepton. One of the predictions of the SM is that neutrino masses are exactly zero, but a little over 25 years ago, neutrino experiments revealed that this is not exactly true. Neutrinos have tiny but undeniably nonzero masses.

Mixing it up

The search for neutrino masses is almost as old as Pauli’s 93-year-old postulate that neutrinos exist. They were ultimately discovered around the turn of the millennium through the observation of neutrino flavour oscillations. It turns out that we can produce one of the neutrino flavours (for example ν_μ) and later detect it as a different flavour (for example ν_e) so long as we are willing to wait for the neutrino flavour to change. The probability associated with this phenomenon oscillates in spacetime with a characteristic distance that is inversely proportional to the differences of the squares of the neutrino masses. Given the tininess of neutrino masses and mass splittings, these distances are frequently measured in hundreds of kilometres in particle-physics experiments.

Neutrino oscillations also require the leptons to mix. This means that the neutrino flavour states are not particles with a well defined mass but are quantum superpositions of different neutrino states with well defined masses. The three mass eigenstates are related to the three flavour eigenstates via a three-dimensional mixing matrix, which is usually parameterised in terms of mixing angles and complex phases.

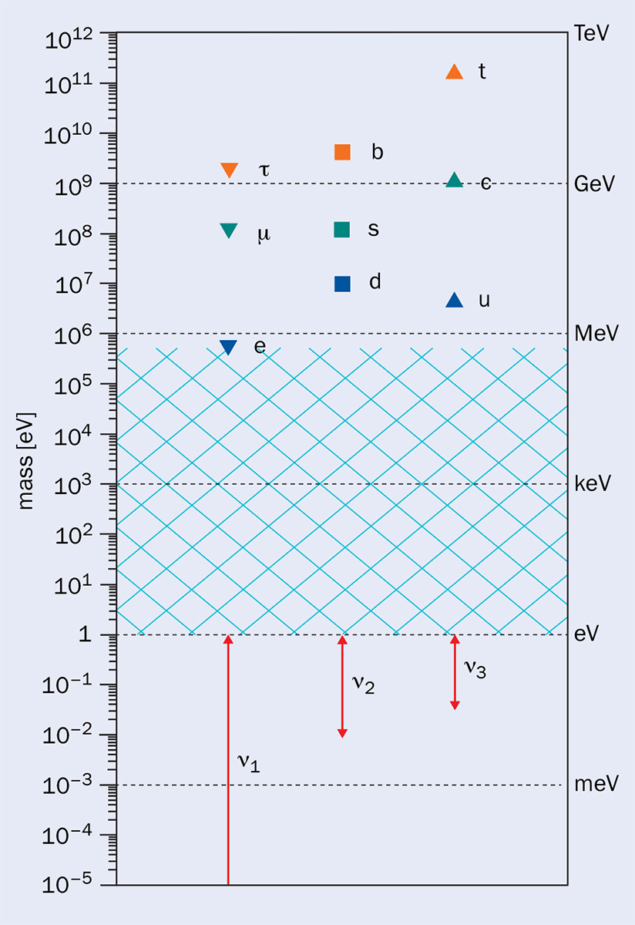
In the last few decades, precision measurements of neutrinos produced in the Sun, in the atmosphere, in nuclear reactors and in particle accelerators in different parts of the world, have measured the mixing parameters at the several percent level. Assuming the mixing matrix is unitary, all but one have been shown to be nonzero. The measurements have revealed that the three neutrino mass eigenvalues are separated by two different mass-squared differences: a small one of order 10^–4 eV² and a large one of order 10^–3 eV². Data therefore reveal that at least two of the neutrino masses are different from zero. At least one of the neutrino masses is above 0.05 eV, and the second lightest is at least 0.008 eV. While neutrino oscillation experiments cannot measure the neutrino masses directly, precise measurements of beta-decay spectra and constraints from the large-scale structure of the universe offer complementary upper limits. The nonzero neutrino masses are constrained to be less than roughly 0.1 eV.

These masses are tiny when compared to the masses of all the other particles (see “Chasm” figure). The mass of the lightest charged fermion, the electron, is of order 10⁶ eV. The mass of the heaviest fermion, the top quark, is of order 10¹¹ eV, as are the masses of the W, Z and Higgs bosons. These particle masses are all at least seven orders of magnitude heavier than those of the neutrinos. No one knows why neutrino masses are dramatically smaller than those of all other massive particles.

The Standard Model and mass

To understand why the SM predicts neutrino masses to be zero, it is necessary to appreciate that particle masses are complicated in this theory. The reason is as follows. The SM is a quantum field theory. Interactions between the fields are strictly governed by their properties: spin, various “local” charges, which are conserved in interactions, and – for fermions like the neutrinos, charged leptons and quarks – another quantum number called chirality.

In quantum field theories, mass is the interaction between a right-chiral and a different left-chiral field. A naive picture is that the mass-interaction constantly converts left-chiral states into right-chiral ones (and vice versa) and the end result is a particle with a nonzero mass. It turns out, however, that for all known fermions, the left-chiral and right-chiral fermions have different charges. The immediate consequence of this is that you can’t turn one into the other without violating the conservation of some charge so none of the fermions are allowed to have mass: the SM naively predicts that all fermion masses are zero!

The Higgs field was invented to fix this shortcoming. It is charged in such a way that some right-chiral and left-chiral fermions are allowed to interact with one another plus the Higgs field which, uniquely among all known fields, is thought to have been turned on everywhere since the phase transition that triggered electroweak symmetry breaking very early in the history of the universe. In other words, so long as the vacuum configuration of the Higgs field is not trivial, fermions acquire a mass thanks to these interactions.

This is not only a great idea; it is also at least mostly correct, as spectacularly confirmed by the discovery of the Higgs boson a little over a decade ago. It has many verifiable consequences. One is that the strength with which the Higgs boson couples to different particles is proportional to the particle ’s mass – the Higgs prefers to interact with the top quark or the Z or W bosons relative to the electron or the light quarks. Another consequence is that all masses are proportional to the value of the Higgs field in the vacuum (10¹¹ eV) and, in the SM, we naively expect all particle masses to be similar.

Neutrino masses are predicted to be zero because, in the SM, there are no right-chiral neutrino fields and hence none for the left-chiral neutrinos – the ones we know about – to “pair up” with. Neutrino masses therefore require the existence of new fields, and hence new particles, beyond those in the SM.

Wanted: new fields

The list of candidate new fields is long and diverse. For example, the new fields that allow for nonzero neutrino masses could be fermions or bosons; they could be neutral or charged under SM interactions, and they could be related to a new mass scale other than the vacuum value of the SM Higgs field (10¹¹ eV), which could be either much smaller or much larger. Finally, while these new fields might be “easy” to discover with the current and near-future generation of experiments, they might equally turn out to be impossible to probe directly in any particle-physics experiment in the foreseeable future.

Though there are too many possibilities to list, they can be classified into three very broad categories: neutrinos acquire mass by interacting with the same Higgs field that gives mass to the charged fermions; by interacting with a similar Higgs field with different properties; or through a different mechanism entirely.

At first glance, the simplest idea is to postulate the existence of right-chiral neutrino fields and further assume they interact with the Higgs field and the left-chiral neutrinos, just like right-chiral and left-chiral charged leptons and quarks. There is, however, something special about right-chiral neutrino fields: they are completely neutral relative to all local SM charges. Returning to the rules of quantum field theory, completely neutral chiral fermions are allowed to interact “amongst themselves” independent of whether there are other right-chiral or left-chiral fields around. This means the right-chiral neutrino fields should come along with a different mass that is independent from the vacuum value of the Higgs field of 10¹¹ eV.

To prevent this from happening, the right-chiral neutrinos must possess some kind of conserved charge that is shared with the left-chiral neutrinos. If this scenario is realised, there is some new, unknown fundamental conserved charge out there. This hypothetical new charge is called lepton number: electrons, muons, tau leptons and neutrinos are assigned charge plus one, while positrons, antimuons, tau antileptons and antineutrinos have charge minus one. A prediction of this scenario is that the neutrino and the antineutrino are different particles since they have different lepton numbers. In more technical terms, the neutrinos are massive Dirac fermions, like the charged leptons and the quarks. In this scenario, there are new particles associated with the right-chiral neutrino field, and a new conservation law in nature.

Accidental conservation

As of today, there is no experimental evidence that lepton number is not conserved, and readers may question if this really is a new conservation law. In the SM, however, the conservation of lepton number is merely “accidental” – once all other symmetries and constraints are taken into account, the theory happens to possess this symmetry. But lepton number conservation is no longer an accidental symmetry when right-chiral neutrinos are added, and these chargeless and apparently undetectable particles should have completely different properties if it is not imposed.

If lepton number conservation is imposed as a new symmetry of nature, making neutrinos pure Dirac fermions, there appears to be no observable consequence other than nonzero neutrino masses. Given the tiny neutrino masses, the strength of the interaction between the Higgs boson and the neutrinos is predicted to be at least seven orders of magnitude smaller than all other Higgs couplings to fermions. Various ideas have been proposed to explain this remarkable chasm between the strength of the neutrino’s interaction with the Higgs field relative to that of all other fermions. They involve a plurality of theoretical concepts including extra-dimensions of space, mirror copies of our universe and dark sectors.

A second possibility is that there are more Higgs fields in nature and that the neutrinos acquire a mass by interacting with a Higgs field that is different from the one that gives a mass to the charged fermions. Since the neutrino mass is proportional to the vacuum value of a different Higgs field, the fact that the neutrino masses are so small is easy to tolerate: they are simply proportional to a different mass scale that could be much smaller than 10¹¹ eV. Here, there are no right-chiral neutrino fields and the neutrino masses are interactions of the left-chiral neutrino fields amongst themselves. This is possible because, while the neutrinos possess weak-force charge they have no electric charge. In the presence of the nontrivial vacuum of the Higgs fields, the weak-force charge is effectively not conserved and these interactions may be allowed. The fact that the Higgs particle discovered at the LHC – associated with the SM Higgs field – does not allow for this possibility is a consequence of its charges. Different Higgs fields can have different weak-force charges and end up doing different things. In this scenario, the neutrino and the antineutrino are, in fact, the same particle. In more technical terms: the neutrinos are massive Majorana fermions.

Neutrino masses require the existence of new fields, and hence new particles, beyond those in the Standard Model

One way to think about this is as follows: the mass interaction transforms left-chiral objects into right-chiral objects. For electrons, for example, the mass converts left-chiral electrons into right-chiral electrons. It turns out that the antiparticle of a left-chiral object is right-chiral and vice versa, and it is tempting to ask whether a mass interaction could convert a left-chiral electron into a right-chiral positron. The answer is no: electrons and positrons are different objects and converting one into the other would violate the conservation of electric charge. But this is no barrier for the neutrino, and we can contemplate the possibility of converting a left-chiral neutrino into its right-chiral antiparticle without violating any known law of physics. If this hypothesis is correct, the hypothetical lepton-number charge, discussed earlier, cannot be conserved. This hypothesis is experimentally neither confirmed nor contradicted but could soon be confirmed with the observation of neutrinoless double-beta decays – nuclear decays which can only occur if lepton-number symmetry is violated. There is an ongoing worldwide campaign to search for the neutrinoless double-beta decay of various nuclei.

A new source of mass

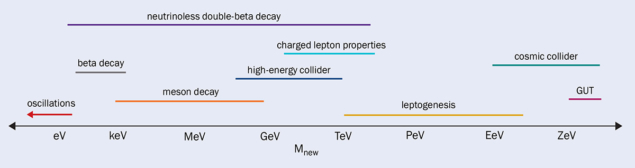
In the third category, there is a source of mass different from the vacuum value of the Higgs field, and the neutrino masses are an amalgam of the vacuum value of the Higgs field and this new source of mass. A very low new mass scale might be discovered in oscillation experiments, while consequences of heavier ones may be detected in other types of particle-physics experiments, including measurements of beta and meson decays, charged-lepton properties, or the hunt for new particles at high-energy colliders. Searches for neutrinoless double-beta decay can reveal different sources for lepton-number violation, while ultraheavy particles can leave indelible footprints in the structure of the universe through cosmic collisions. The new physics responsible for nonzero neutrino masses might also be related to grand-unified theories or the origin of the matter–antimatter asymmetry of the universe, through a process referred to as leptogenesis. The range of possibilities spans 22 orders of magnitude (see “eV to ZeV” figure).

Challenging scenarios

Since the origin of the neutrino masses here is qualitatively different from that of all other particles, the values of the neutrino masses are expected to be qualitatively different. Experimentally, we know that neutrino masses are much smaller than all charged- fermion masses, so many physicists believe that the tiny neutrino masses are strong indirect evidence for a source of mass beyond the vacuum value of the Higgs field. In most of these scenarios, the neutrinos are also massive Majorana fermions. The challenge here is that if a new mass scale exists in fundamental physics, we know close to nothing about it. It could be within direct reach of particle-physics experiments, or it could be astronomically high, perhaps as large as 10¹² times the vacuum value of the SM’s Higgs field.

Searching for neutrinoless double-beta decay is the most promising avenue to reveal whether neutrinos are Majorana or Dirac fermions

How do we hope to learn more? We need more experimental input. There are many outstanding questions that can only be answered with oscillation experiments. These could provide evidence for new neutrino-like particles or new neutrino interactions and properties. Meanwhile, searching for neutrinoless double-beta decay is the most promising avenue to experimentally reveal whether neutrinos are Majorana or Dirac fermions. Other activities include high-energy collider searches for new Higgs bosons that like to talk to neutrinos and new heavy neutrino-like particles that could be related to the mechanism of neutrino mass generation. Charged-lepton probes, including measurements of the anomalous magnetic moment of muons and searches for lepton-flavour violation, may provide invaluable clues, while surveys of the cosmic microwave background and the distribution of galaxies could also reveal footprints of the neutrino masses in the structure of the universe.

We still know very little about the new physics uncovered by neutrino oscillations. Only a diverse experimental programme will reveal the nature of the new physics behind the neutrino mass puzzle.