Major surprises from the world’s first proton–proton collider.

Our understanding of QCD continues to depend on the contributions from totally unexpected results found at the Intersecting Storage Rings (ISR). Some of the most relevant of these also represent an interesting frontier for research at the LHC. In particular, the “effective energy” remains the basic parameter for revealing the features of universality in the multiparticle hadronic systems that are produced, while the “leading” effect is still present at LHC energies, with all of its consequences, such as the total independence of the two hemispheres of the interaction.
Effective energy
The perceived wisdom, up to the moment when the first unexpected results came from the ISR, was that each pair of strongly interacting particles produces its own final state. The properties of these final states were measured to be all different, as shown by a remarkable number of well established quantities, namely: the fractional momentum distribution dσ/dxF (where xF is Feynman x); the average number of charged particles < nch >; the ratio of the average energy in the charged channel to the total energy < Ech >/< Etotal >; the transverse-momentum distributions dσ/dpT2; the normalized transverse-momentum distribution dσ/(dσ/pT /< pT >); the event planarity; the two-particle correlations; and the scale-breaking effects.
Out of these eight quantities, the most popular is the average number of charged particles, < nch >. It was taken for granted that different pairs of interacting particles – πp, Kp, pp, p–p, etc. – had to give different values for < nch >. That the other seven quantities were different for different pairs of interacting particles was considered a natural consequence of the fact that different initial states have to produce different final states. This perceived wisdom was shown to be wrong when the effective energy was discovered at the ISR.
At the ISR, and at any other collider, the quantity √s = √(q1inc + q2inc)2 = 2Einc was considered to be the total energy available in the centre-of-mass system (Einc being the incident energy of each colliding proton). The Bologna-CERN-Frascati (BCF) group proved that this is not true: the quantity √s should be considered as the “nominal”, not the “effective”, value for the total energy available.
The key point is that in a pp collision, such as at the ISR, the total energy available for particle production is not (√s)pp = 2Einc. In fact, the incoming proton can carry a large fraction of the primary energy away into the final state. If you examine the final state of a pp interaction, in 90% of the cases you find in each hemisphere a “leading” particle: q1leading and q2leading. On average, they carry 50% of the nominal energy, 2Einc. The hadronic system produced in each hemisphere has at its disposal the quadrimomentum qhad = qinc – qleading, which gives rise to the quantity 2Ehad. This is the effective energy.
The BCF group measured the detailed features of 105 pp collisions, on an event-by-event basis, to identify the effective energy of each collision. Once this quantity is taken as the correct energy for a given process, the eight quantities quoted above are the same, no matter what the nature of the pairs of interacting particles or the type of interaction. The leading effect is a very general phenomenon that is present when a hadron interacts – whether strongly, electromagnetically or weakly (Basile et al. 1981a and 1981b). When a hadron in the final state shares energy with all other particles produced in this highly privileged way, the effect must be accounted for correctly to compare the properties of the multiparticle hadronic system produced in the interaction. This is how we found the first evidence for universality features between pp and e+e– data using pp interactions at the nominal ISR energy, (√s)pp = 62 GeV (Basile et al. 1980).
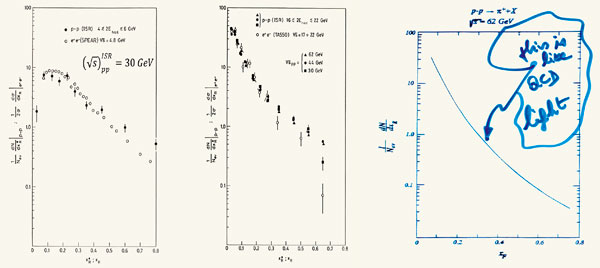
As figure 1 (p39) indicates, this fixed nominal energy corresponds to a set of effective energies available for particle production, 2Ehad, in a range of about 5–40 GeV. We collected data at three ISR energies, (√s)pp = 30, 44, and 62 GeV for the following reason. It was crucial to show that the multiparticle hadronic systems produced in pp interactions with the same values of 2Ehad, but with different values of Einc, had the same properties in terms of the eight quantities mentioned above.
Let us take one example. The BCF group discovered that the fractional momentum distribution, dσ/dxF, of a pion produced in the reaction pp→π+ + X at the nominal total energy (√s)pp = 62 GeV is the sum of the fractional momentum distributions at different effective energies (figure 2). This is why Vladimir Gribov liked to call the pion spectrum the “QCD-light”.
The effective energy also dismantled another myth, the one that gave a special role to “high” transverse-momentum phenomena. We found at the ISR that the multiparticle systems (jets) produced at high pT and at low pT show the same universality features (Basile et al. 1988).
The leading effect
The discovery of effective energy was the driving force to study in detail the leading effect, which is a basic non-perturbative QCD phenomenon. In another impressive set of totally unexpected results, the BCF group at the ISR established the following five properties of the effect, which need to be explained by QCD.
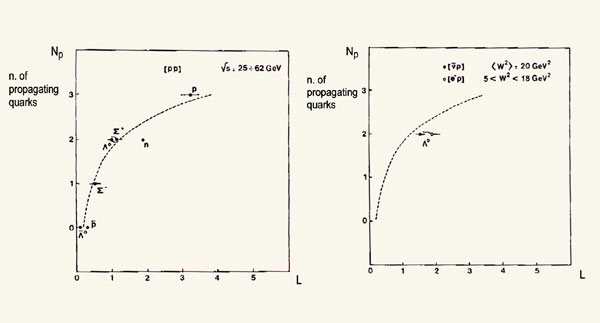
1. The leading effect depends on the quantum number flow. For example, if in the initial state there is a proton (uud) that goes into the final state, the probability of having the same “proton” (uud) with more energy-momentum than all the other particles is very high. The proof is in figure 3a, which shows how the number of quarks that go from the initial to the final state varies with the value of a function, L, which is proportional to the probability of having the particle in the privileged leading status with respect to all other particles in the final state. The leading effect decreases with the number of propagating quarks from the initial to the final state. For example, when the process is p(uud) → p(uud), all three quarks of the initial state go into the final state and L _˜ 3. However, in both p(uud) → Λ0(uds) and p(uud) → Σ+(uus) there are two propagating quarks and L _˜ 1. For p(uud) → Σ0(dds) there is only one propagating quark and L _˜ 0.5. The minimum value of L is when there are no quarks going from the initial to the final state.
2. The leading effect is flavour independent. The neutron, produced in the process p(uud) → n(udd), seems to indicate some deviation from the other cases with two propagating quarks in figure 3a. To study if there is a flavour dependence in the leading effect, we extended our research to all heavy flavours. This is how we discovered the leading production of Λc+ (Basile et al. 1981c) and found for the first time the Λb0, which at the time was the heaviest particle known (Basile et al. 1981d). The search for the Λb0 proved that the leading production mechanism is valid also for the Λb0 and that the same leading-baryon effect is present in the Λb0, Λc+ and Λs0 production mechanisms. So, despite the large mass difference between the strange (s), the charm (c), and the beauty (b) quarks, the production of these differently flavoured baryonic states shows the same leading effect (Basile et al. 1981e). The conclusion is that there is no mass-dependence in the leading effect and that it is flavour-invariant.
3. The leading effect is present in deep inelastic scattering (electromagnetic and weak). Figure 3b shows two examples of deep inelastic scattering: one is electromagnetic (e–p) and the other is weak (ν–p). In both cases the leading effect is present. Taking into account the results previously reported, where the interactions were all strong, the data prove that no matter if the interaction is strong, electromagnetic or weak, the leading effect is there and depends on the flow of quantum numbers from the initial to the final state.
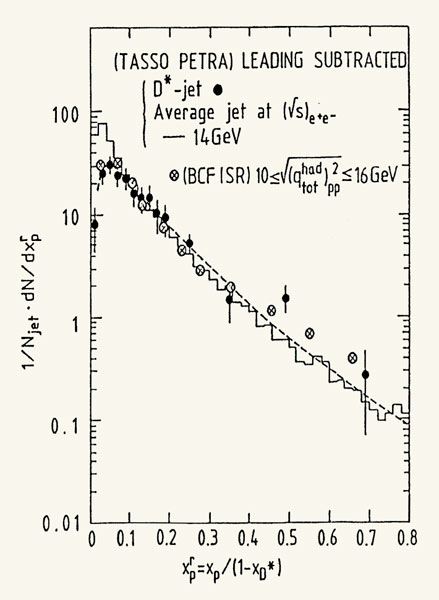
4. The leading effect also exists when there are no hadrons in the initial state, as in e+e– annihilation. The fractional momentum distribution measured by the TASSO experiment of the particles produced in e+e– annihilation at √s = 34.4 GeV at the PETRA collider deviated markedly from the expected spectrum when a leading D* was present in the final state. Using pp data from the ISR at effective energies in the range 10–16 GeV, the TASSO data showed excellent agreement (figure 4). The only correction needed was the subtraction of the D* leading effect.
5. There are no long-range correlations in the leading effect. For many years experimental data have given evidence for a correlation between the two ISR hemispheres. The same problem needs to be studied at the LHC. The BCF group proved that these correlations disappear when the data are analysed in terms of the effective energy. The best proof came from the study of p1inc + p2inc → p1leading + p2leading + anything, where p1,2inc indicate the two incident protons, and p1,2leading the two leading protons. The data-taking was performed using unbiased events to have a set of genuine inclusive pp interactions. The results, shown in figure 5, prove that the two hemispheres are totally independent and – contrary to what had been believed before – there are no long-range correlation effects.
Two final remarks should be made on the leading effect. First, when there is no quantum number flow from the initial to the final state, the leading effect depends on the probability that the fragmentation products recombine themselves into one leading particle. From high-pT data at the ISR we have: σ(single particle) ETinclusive/σ(jet) ETinclusive ≈ 10–2 for ET _˜ 5–10 GeV; from e+e– annihilation the results are: σ(e+e– → D* + other particles)/σ(e+e– → C + other particles) ≈ 10–2. We can deduce that if a single particle carries a large part of a certain available energy, it must “pay” a factor of around 10–2. How this recombination into one leading particle can be possible is a problem for non-perturbative QCD theorists.

A second point is that in pp interactions at ISR energies, about 20 mb of cross-section is in the leading effect. At the ISR this effect is dominated by the quantum number flow. In e+e– there is no quantum number flow from the initial to the final state and only about 1% of the total cross-section is in the leading effect. For an explanation we must wait until non-perturbative QCD can give the correct “predictions”.
In conclusion
The ISR were the source of a series of totally unexpected results. The effective energy with its universality features plays a fundamental role in all QCD processes. The leading effect is flavour independent, has no long-range correlation and exists no matter whether the process originates in a strong, electromagnetic or weak interaction. The next frontier is to find out if these properties are still valid at LHC energies.