Channelling of particles by the arrangement of atoms in crystals has been known for many decades. The effect is nowadays used in accelerators to steer high-energy beams, which are guided by the strong coherent electric field arising from the nuclear charges in bent crystals. Some 20 years ago, Alexander Taratin and S A Vorobiev predicted that the coherent field of a bent crystal could also reflect particles through small angles (Taratin and Vorobiev 1987). It was only in 2006, however, that experiments with 1 GeV and 70 GeV protons made the first observation and measurement of this “volume reflection” effect (Ivanov et al. 2006). A year later, a team at CERN’s SPS reported a nice demonstration of the effect with 400 GeV protons.
These studies have found that the range of entrance angles over which ions undergo volume reflection can be much greater than the critical angle of channelling. Furthermore, the experiment at the SPS showed that the probability of reflection far exceeds that of channelling. It is still less than 100%, however, because some particles “stick” to the atomic planes instead of bouncing back – because incoherent scattering (volume capture) traps them into channelled states.
A single-volume reflection at the energy of the SPS is of the order of 14 μrad. It is possible to obtain greater deflection by reflecting the particles from several bent-crystal layers, as figure 1 indicates. This leads to a multiple-volume reflection (MVR) angle that increases in proportion to the number of layers (Taratin and Scandale 2007, Breese and Biryukov 2007). One experimental limitation is that some particles are volume captured with every reflection, therefore reducing the number of reflected particles linearly with the number of reflections, N.
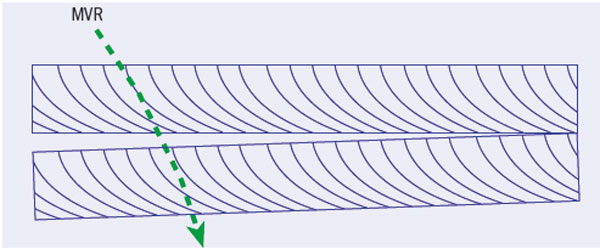
Computer simulations have shown two ways to overcome this limitation and increase the reflection efficiency to remarkably high values (Biryukov and Breese 2007). One way is to arrange each subsequent bent layer to reflect the complete distribution of particles passing through the layer above, including the tail of volume-captured particles. Simulations show that, in this case, the MVR angle grows linearly with N, while the efficiency remains constant, limited mainly by the volume capture in the last layer. The second way to increase reflection efficiency is to suppress the volume-capture process itself. The volume-captured particles occupy the top of the potential well and are easily affected by variations in the crystal curvature – an effect already known from experiments at 70 GeV and from theory. To suppress fully the few per cent probability of volume capture observed in single-volume reflection, the curvature should vary significantly over the length of the crystal so that it quickly releases most of the volume-captured particles.
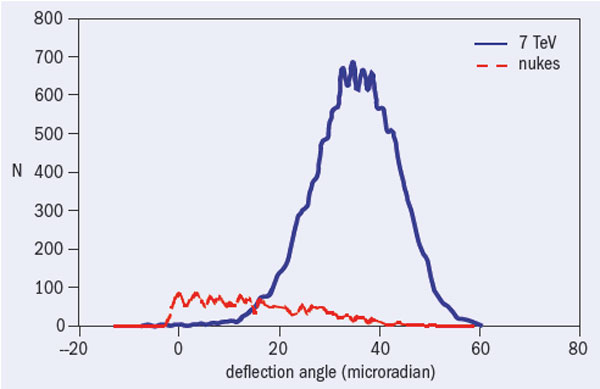
Computer studies of 7 TeV protons show that the rate of volume capture is suppressed by a factor of 20 in a silicon crystal, in which the curvature varies by 40% along its length compared to the same crystal with a constant curvature. Figure 2 shows a 7 TeV proton beam bent through an angle of about 40 μrad, which could serve well for collimation purposes at the LHC. Here, a structure comprising 20 (110) layers of silicon, each bent through 65 μrad with a radius of 50 m, has deflected 7 TeV protons with an efficiency of 99.95%. This efficiency level by far outperforms the capabilities of channelling in crystals and the angular acceptance of this structure is 65 μrad, which is around 20 times greater than the acceptance of bent-crystal channelling. Such perfect deflection efficiency over a broad angular acceptance makes MVR ideal for collimation.
The near-100% deflection efficiency obtained in the single encounter of a particle with the multilayered structure may be important in many types of accelerators, including linear machines (such as a future International Linear Collider), machines with a short beam lifetime (such as muon or short-cycle machines) and in high-intensity beams with a fast-developing instability. The possibility of an efficiency of close to 100% makes MVR attractive for high-intensity beam applications, where beam losses usually rule out the use of bent-crystal channelling.
At an energy of 7 TeV, the crystal material along the beam direction in this example becomes as long as 6.5 cm. Some protons undergo inelastic nuclear interactions in the crystal layers. Figure 2 shows the deflection angle for these protons at the moment of nuclear interaction. On average they are bent by half the bending angle of non-interacting protons, with a bending efficiency of a remarkably high 95%. This is different behaviour compared to both an amorphous target and to bent-crystal channelling, where the products of nuclear interactions move in a forward direction. When using MVR for collimation, not only are the primary particles bent towards an absorber but the debris of the particles that have interacted with the crystal nuclei are also bent towards an absorber with high efficiency.
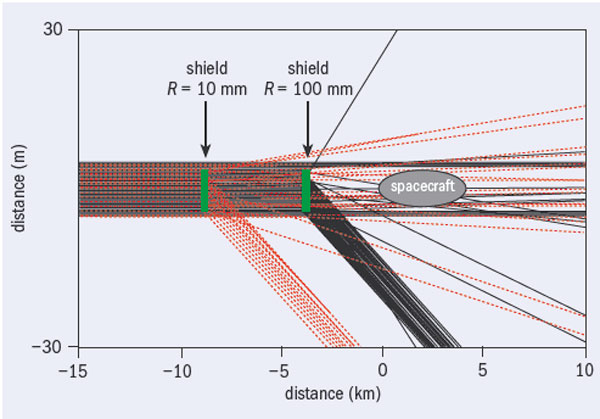
MVR also provides an attractive mechanism for a space shield that can deflect ions with energies of mega- or giga-electron volts per nucleon. Here, highly efficient deflection over a range of entrance angles at high energies is of paramount importance for the design of a space shield for radiation protection that is based on curved crystals. Such a bent-crystal shield was recently proposed for deflecting cosmic-radiation ions of all atomic numbers away from spacecraft (Breese 2007). A team at the National University of Singapore fabricated a bent-crystal shield with a surface area of 1 × 1 cm2 that is capable of deflecting ions with energies of up to 100 GeV/nucleon. Figure 3 shows the simulated results of the crystal shield protecting a spacecraft from high-energy ions approaching from a single direction. This adds yet another link between the microcosm of a particle-physics laboratory and the macrocosm of space travel.