DIRAC observes dimeson atoms and measures their lifetime

The study of nonstandard atoms has a long tradition in particle physics. Such exotic atoms include positronium, muonic atoms, antihydrogen and hadronic atoms. In this last category, mesonic hydrogen in particular has been investigated extensively in different experiments at CERN, PSI and Frascati. Dimeson atoms also belong to this category. These electromagnetically bound mesonic pairs, such as the π⁺π^– atom (pionium, A_2π) or the πK atom (A_πK), offer the opportunity to study the theory of the strong interaction, QCD, at low energy, i.e. in the confinement region.

This strong interaction leads to a broadening and a shift of atomic levels, and dominates the lifetime of these exotic atoms in their s-states. The ππ interaction at low energy, constrained by the approximate chiral symmetry SU(2) for two flavours (u and d quarks), is the simplest and best understood hadron–hadron process. Since the bound-state physics is well known, a measurement of the A_2π lifetime provides information on hadron properties in the form of scattering lengths – the basic parameters in low-energy ππ scattering.

Moreover, the low-energy interaction between the pion and the next lightest, and strange, meson – the kaon – provides a promising probe for learning about the more general three-flavour SU(3) structure (u, d and s quarks) of hadronic interactions, which is a matter not directly accessible in pion–pion interactions. Hence, data on πK atoms are valuable because they provide insights into the role played by the strange quarks in the QCD vacuum.

The experiment

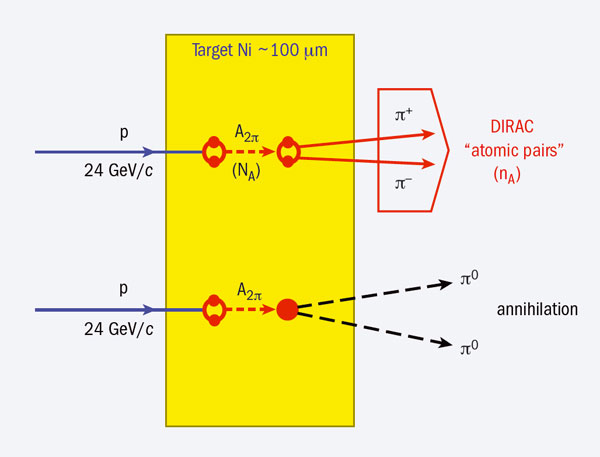
The mesonic atoms A_2π (A_πK) are produced by final-state Coulomb interactions between oppositely charged ππ (πK) pairs that are generated in proton–target reactions (Nemenov 1985). In the DImeson Relativistic Atom Complex (DIRAC) experiment at CERN, they are formed when a 24 GeV/c proton beam from the Proton Synchrotron hits a thin target, typically a 100 μm-thick nickel foil (figure 1). After production, the mesonic atoms travel through the target and some of them are broken up (ionized) as they interact with matter. This produces “atomic pairs”, which are characterized by their small relative momenta, Q < 3 MeV/c, in the centre of mass of the pair. These pairs are detected in the DIRAC apparatus. The remaining atoms mainly annihilate into π⁰π⁰ pairs, which are not detected, or they survive and annihilate later. The number of “atomic pairs” from the break-up of atoms, n_A, depends on the annihilation mean-free-path, which is given by the atom’s lifetime, τ, and its momentum. Thus, the break-up probability, P_br, is a function of the A_2π’s lifetime, τ.

The interactions between the protons and the target also produce oppositely charged free ππ pairs, both with and without final-state Coulomb interactions, depending on whether or not the pairs are produced close to each other. This gives rise to “Coulomb pairs” and “non-Coulomb pairs”. The latter includes meson pairs in which one or both mesons come from the decay of long-lived sources. Furthermore, two mesons from different interactions can contribute as “accidental pairs”. The total number of atoms produced, N_A, is proportional to N_C, the number of Coulomb pairs with low relative momenta, N_A = kN_C, where the coefficient, k, is precisely calculable. DIRAC measures the break-up probability for the A_2π, which is defined as the ratio of the observed number of “atomic pairs” to the number of produced atoms: P_br(τ)= n_A/N_A. N_A is calculated from the number of “Coulomb pairs”, N_C, obtained from fits to the data.

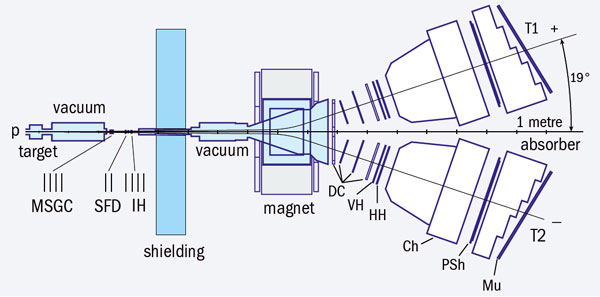
The purpose of the DIRAC set-up is to record oppositely charged ππ (πK) pairs with small relative momenta, Q. As figure 2 shows, the emerging pairs of charged pions travel in vacuum through the upstream part where co-ordinate and ionization detectors provide initial track data, before they are split by the 2.3 Tm bending magnet into the “positive” (T1) and “negative” (T2) arms. Both arms are equipped with high-precision drift chambers and trigger/time-of-flight detectors, as well as Cherenkov, preshower and muon counters. The relative time resolution between the two arms is around 200 ps.

The momentum reconstruction in the double-arm spectrometer uses the drift chamber information from both arms as well as the measured hits in the upstream co-ordinate detectors. The resolution on the longitudinal (Q_L) and transverse (Q_T) components of the relative momentum of the pair, Q, defined with respect to the direction of the total momentum of the pair in the laboratory, is 0.55 MeV/c and 0.1 MeV/c, respectively. A system of fast-trigger processors selects the all-important events with small Q.

Observing and measuring lifetimes

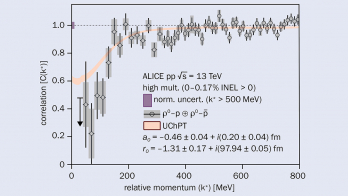
The observation of the A_2π was reported from an experiment at Serpukhov nearly 20 years ago. This was followed at CERN 10 years later with a measurement of the A_2π lifetime by DIRAC (Adeva et al. 2005). Last autumn, DIRAC presented the most recent value for the A_2π lifetime in the ground state, τ = 3.15 × 10^–15 s, with a total uncertainty of around 9%, based on the statistics of 21 200 “atomic pairs” collected with the nickel target in 2001–2003 (Adeva et al. 2011). Figure 3 (overleaf) shows the characteristic accumulation of events at low Q_L from the break-up of the π⁺π^– atom: the A_2π signal appears as an excess of pairs over the background spectrum in the low Q region.

S-wave ππ scattering is isospin-dependent, so this lifetime can be used to calculate a scattering-length difference, |a₀–a₂|, where a₀ and a₂ are the S-wave ππ scattering lengths for isospin 0 and 2, respectively. The measured lifetime yields a result of |a₀–a₂| = 0.253 (m_π^–1) with around 4% precision, in agreement with the result obtained by the NA48/2 experiment at CERN (Batley et al. 2009). The corresponding theoretical values are 0.265 ± 0.004 (m_π^–1) for the scattering-length difference (Colangelo et al. 2000) and (2.9 ± 0.1) × 10^–15 s for the lifetime (Gasser et al. 2001). These results demonstrate the high precision that can be reached in low-energy hadron interactions, in both experiment and theory.

The first evidence for the observation of the πK atom, A_πK, was published by the DIRAC collaboration in 2009 (Adeva et al. 2009). In this case, the mesonic atoms were produced in a 26 μm-thick platinum target and the DIRAC spectrometer had been upgraded for K identification with heavy-gas (C₄F₁₀) and aerogel Cherenkov detectors. An enhancement observed at low relative momentum corresponds to the production of 173 ± 54 πK “atomic pairs”. From this first data sample, the collaboration derived a lower limit on the πK atom lifetime of τ_πK > 0.8 × 10^–15 s (90% CL), to be compared with the theoretical prediction of (3.7 ± 0.4) × 10^–15 s (Schweizer 2004). The ongoing detailed analysis of a much larger data sample aims first to extract a clear signal for the production of the A_πK atom and then to deduce from these data a value for the A_πK lifetime.

Future investigations

Pionium is an atom like hydrogen and the properties of its states vary strongly with their quantum numbers. An illustration of this is the 2s→1s two-photon de-excitation in hydrogen (τ_2s ≈ 0.1s), which is many orders of magnitude slower than the 2p→1s radiative transition (τ_2p = 1.6 ns). In pionium, the situation is similar but opposite: the decay A_2π (2s-state)→2π⁰ (τ_2s = 23.2 fs) is roughly three orders of magnitude faster than the 2p→1s radiative transition (τ_2p = 11.7 ps). The DIRAC collaboration aims to measure Lamb shifts in pionium by exploiting the properties of these specific states and in 2010 started to study the possibility of observing long-lived A_2π states (Nemenov et al. 2002).

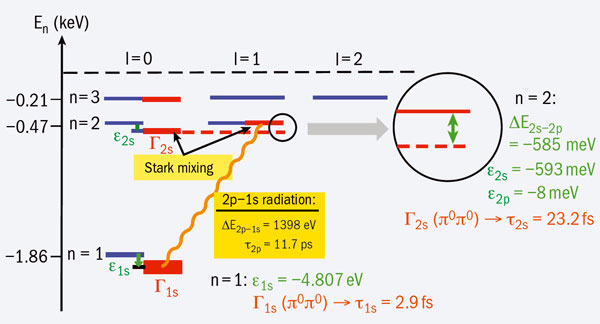
The energy shifts, ΔE_ns–np, for levels with the principal quantum number, n, and orbital quantum number, l, are another valuable source of information. These shifts contain a dominant strong contribution, ΔE^strong _ns–np, together with minor QED contributions, ΔE^QED _ns–np, from vacuum polarization and self-energy effects. The strong s-state energy shift,ΔE^strong _ns–np, is proportional to (2a₀+a₂), i.e. it depends on the same scattering lengths, a₀ and a₂, as the pionium lifetime. As figure 4 shows, for the principal quantum number n=2, the strong and electromagnetic interactions shift the 2s level below the 2p level by ΔE_2s–2p = ΔE^strong _ns–np + ΔE^QED _2s–2p = – 0.47 eV – 0.12 eV = – 0.59 eV (Schweizer 2004).

By studying the dependence of the lifetime of long-lived A_2π (with l≥1) on an applied electric field – the Stark-mixing effect – the DIRAC experiment is in a unique position to investigate the splitting of pionium energy levels. This will allow another combination of pion-scattering lengths to be extracted, so that a₀ and a₂ can finally be determined individually.