CMS weighs in on flavour anomalies

A report from the CMS experiment

Recent results from LHCb and other experiments appear to challenge the assumption of lepton-flavour universality. To explore further, the CMS collaboration has recently conducted a new search probing one of the theories that attempts to explain these flavour “anomalies”. Using 77.3 fb^–1 of proton–proton collision data recorded in 2016 and 2017 at a centre-of-mass energy of 13 TeV, the CMS analysis is the first dedicated search for a neutral gauge boson with specific properties that couples only to leptons of the second and third family.

Although the Standard Model (SM) has been successful in describing current experimental results, it is generally believed to be incomplete. It cannot, for example, explain dark matter or the observed asymmetry between matter and antimatter in the universe. There are also several smaller differences between the experiment and the SM prediction that have been building up over the last few years. One set of intriguing anomalies has been reported by LHCb and other dedicated B-physics experiments, indicating a possible lepton-flavour universality violation in B-meson decays (CERN Courier April 2018 p23). Another is the long-standing tension in the measurement of the anomalous magnetic moment of the muon, for which an updated measurement is eagerly awaited (CERN Courier September 2018 p9).

One extension to the SM that has been proposed to explain these anomalies is an enlarged SM gauge group with an additional U(1) symmetry. Spontaneous breaking of this symmetry leads to the prediction of a new massive gauge boson, Zʹ. To keep the extended gauge symmetry free from quantum anomalies, only certain generation-dependent couplings are allowed. The model investigated by CMS promotes the difference in lepton numbers between the second and third generation to a local gauge symmetry, and until now has only been constrained slightly by experiment. Since the predicted Zʹ boson only couples to second- and third-generation leptons, the only way to produce it at the LHC is as final-state radiation off one of these leptons. The ideal source of muons for the purposes of this search is the decay of the SM Z boson to two muons, which can be measured with excellent mass resolution (~1%) in CMS. If a Zʹ boson exists, it will be radiated by one of the muons and decay subsequently to another pair of muons, leading to a final state with four muons.

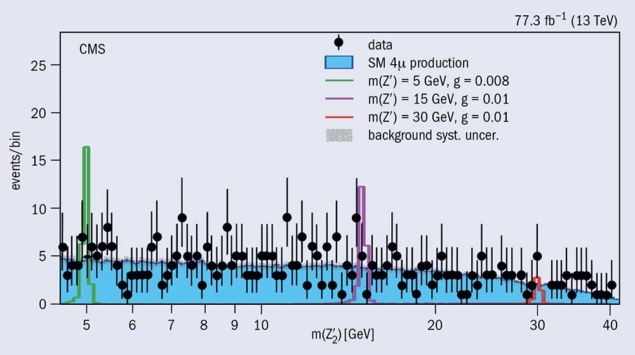
Such a final state is also produced by a rare SM Z-boson decay to four muons mediated by an off-shell photon. The first observation of this rare decay of the SM Z boson in proton–proton collisions was reported by CMS in 2012. In order to reduce this background, the search exploits the resonant character of the new gauge boson’s di-muon decay. Events are selected that contain at least four muons with an invariant mass near the SM Z-boson mass. Di-muon candidates are then formed from muon pairs of opposite sign and a peak in their invariant mass distribution is sought, which would indicate the presence of a Zʹ particle.

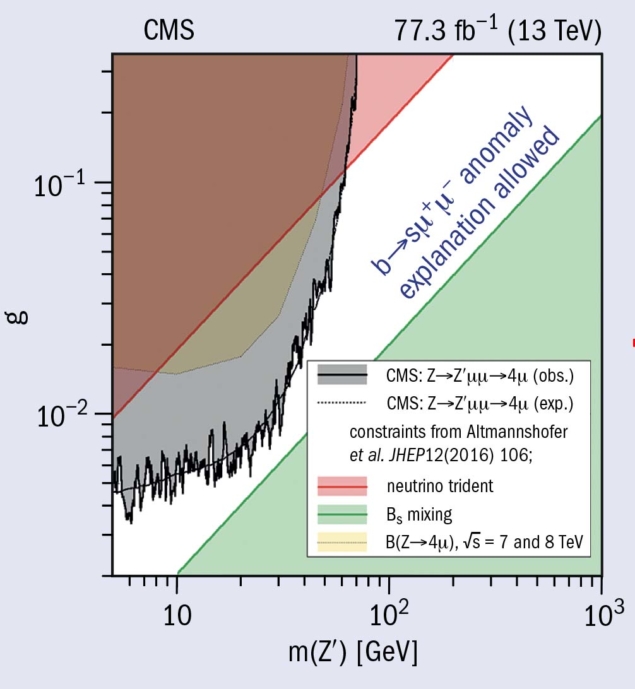
The event yields are found to be consistent with the SM predictions (figure 1). Upper limits of the order of 10⁻⁸–10⁻⁷ are set on the branching fraction of a Z boson decaying to two muons and a Zʹ, with the latter also decaying into two muons, as a function of the Zʹ mass. This can be interpreted as a limit on the Zʹ particle’s coupling strength to muons, and provides the first dedicated limits on these Zʹ models at the LHC. Compared to other experiments and to indirect limits from the LHC obtained at lower centre-of-mass energies during Run 1, this search excludes a significant portion of parameter space favoured by the B-physics anomalies (figure 2). The analysis demonstrates the power and flexibility of the CMS experiment to adapt to and test new incoming physics models, which in turn react to previous experimental results, showing that experiments and theory go hand-in-hand.