Matthew McCullough argues that beyond-the-Standard Model physics may be most strongly expressed in the Higgs self-coupling.
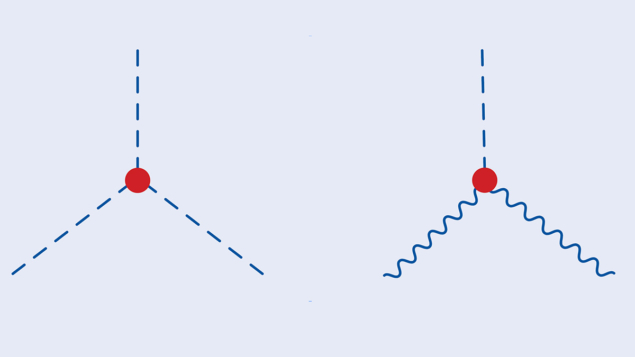
What are the microscopic origins of the Higgs boson? As long as we lack the short-wavelength probes needed to study its structure directly, our best tool to confront this question is to measure its interactions.
Let’s consider two with starkly contrasting experimental prospects. The coupling of the Higgs boson to two Z bosons (HZZ) has been measured with a precision of around 5%, increasing to around 1.3% by the end of High-Luminosity LHC (HL-LHC) operations. The Higgs boson’s self-coupling (HHH) has so far only been measured with a precision of the order of several hundred percent, improving to around the 50% level by the end of HL-LHC operations – though it’s now rumoured that this latter estimate may be too pessimistic.
Good motives
As HZZ can be measured much more precisely than HHH, is it the more promising window beyond the Standard Model (SM)? An agnostic might say that both measurements are equally valuable, while a “top down” theorist might seek to judge which theories are well motivated, and ask how they modify the two couplings. In supersymmetry and minimal composite Higgs models, for example, modifications to HZZ and HHH are typically of a similar magnitude. But “well motivated” is a slippery notion and I don’t entirely trust it.
Fortunately there is a happy compromise between these perspectives, using the tool of choice of the informed agnostic: effective field theory. It’s really the same physical principle as trying to look within an object when your microscope operates on wavelengths greater than its physical extent. Just as the microscopic structure of an atom is imprinted, at low energies, in its multipolar (dipole, quadrupole and so forth) interactions with photons, so too would the microscopic structure of the Higgs boson leave its trace in modifications to its SM interactions.
All possible coupling modifications from microscopic new physics can be captured by effective field theory and organised into classes of “UV-completion”. UV-completions are the concrete microscopic scenarios that could exist. (Here, ultraviolet light is a metaphor for the short-wavelength probes needed to study the Higgs boson’s microscopic origins in detail.) Scenarios with similar patterns are said to live in the same universality class. Families of universality classes can be identified from the bottom up. A powerful tool for this is naïve dimensional analysis (NDA).

One particularly sharp arrow in the NDA quiver is ℏ counting, which establishes how many couplings and/or ℏs must be present in the EFT modification of an interaction. Couplings tell you the number of fundamental interactions involved. ℏs establish the need for quantum effects. For instance, NDA tells us that the coefficient of the Fermi interaction must have two couplings, which the electroweak theory duly supplies – a W boson transforms a neutron into a proton, and then decays into an electron and a neutrino.
For our purposes, NDA tells us that modifications to HZZ must necessarily involve one more ℏ or two fewer couplings than any underlying EFT interaction that modifies HHH. In the case of one more ℏ, modifications to HZZ could potentially be an entire quantum loop factor smaller than modifications to HHH. In the case of two fewer couplings, modifications to HHH could be as large as a factor g2 greater than for HZZ, where g is a generic coupling. Either way, it is theoretically possible that the BSM modifications could be up to a couple of orders of magnitude greater for HHH than for HZZ. (Naively, a loop factor counts as around 1/16 π2 or about 0.01, and in the most strongly interacting scenarios, g2 can rise to about 16 π2.)
Why does this contrast so strongly with supersymmetry and the minimal composite Higgs? They are simply in universality classes where modifications to HZZ and HHH are comparable in magnitude. But there are more universality classes in heaven and Earth than are dreamt of in our well-motivated scenarios.
Faced with the theoretical possibility of a large hierarchy in coupling modifications, it behoves the effective theorist to provide an existence proof of a concrete UV-completion where this happens, or we may have revealed a universality class of measure zero. But such an example exists: the custodial quadruplet model. I often say it’s a model that only a mother could love, but it could exist in nature, and gives rise to coupling modifications a full loop factor of about 200 greater for HHH than HZZ.
When confronted with theories beyond the SM, all Higgs couplings are not born equal: UV-completions matter. Though HZZ measurements are arguably the most powerful general probe, future measurements of HHH will explore new territory that is inaccessible to other coupling measurements. This territory is largely uncharted, exotic and beyond the best guesses of theorists. Not bad circumstances for the start of any adventure.