Jobs – Page 183 of 521

General relativity at 100

Einstein’s long path towards general relativity (GR) began in 1907, just two years after he created special relativity (SR), when the following apparently trivial idea occurred to him: “If a person falls freely, he will not feel his own weight.” Although it was long known that all bodies fall in the same way in a gravitational field, Einstein raised this thought to the level of a postulate: the equivalence principle, which states that there is complete physical equivalence between a homogeneous gravitational field and an accelerated reference frame. After eight years of hard work and deep thinking, in November 1915 he succeeded in extracting from this postulate a revolutionary theory of space, time and gravity. In GR, our best description of gravity, space–time ceases to be an absolute, non-dynamical framework as envisaged by the Newtonian view, and instead becomes a dynamical structure that is deformed by the presence of mass-energy.

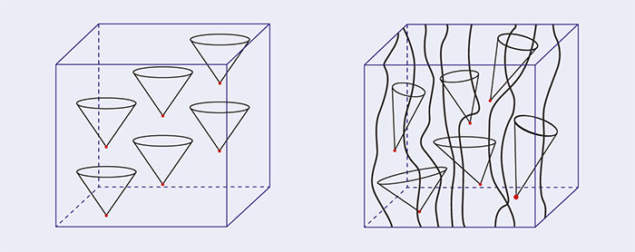
GR has led to profound new predictions and insights that underpin modern astrophysics and cosmology, and which also play a central role in attempts to unify gravity with other interactions. By contrast to GR, our current description of the fundamental constituents of matter and of their non-gravitational interactions – the Standard Model (SM) – is given by a quantum theory of interacting particles of spins 0, ½ and 1 that evolve within the fixed, non-dynamical Minkowski space–time of SR. The contrast between the homogeneous, rigid and matter-independent space–time of SR and the inhomogeneous, matter-deformed space–time of GR is illustrated in figure 1.

Fig. 1. The non-dynamical Minkowski space–time of SR (left) and its regular array of light cones compared to the dynamical, matter-deformed space–time of GR and its field of local light cones (right). GR has been submitted, with striking success, to many high-precision experimental tests.

The universality of the coupling of gravity to matter (which is the most general form of the equivalence principle) has many observable consequences such as: constancy of the physical constants; local isotropy of space; local Lorentz invariance; universality of free fall and universality of gravitational redshift. Many of these have been verified to high accuracy. For instance, the universality of the acceleration of free fall has been verified on Earth at the 10^–13 level, while the local isotropy of space has been verified at the 10^–22 level. Einstein’s field equations (see panel below) also predict many specific deviations from Newtonian gravity that can be tested in the weak-field, quasi-stationary regime appropriate to experiments performed in the solar system. Two of these tests – Mercury’s perihelion advance, and light deflection by the Sun – were successfully performed, although with limited precision, soon after the discovery of GR. Since then, many high-precision tests of such post-Newtonian gravity have been performed in the solar system, and GR has passed each of them with flying colours.

Precision tests

Similar to what is done in precision electroweak experiments, it is useful to quantify the significance of precision gravitational experiments by parameterising plausible deviations from GR. The simplest, and most conservative, deviation from Einstein’s pure spin-2 theory is defined by adding a long-range (massless) spin-0 field, φ, coupled to the trace of the energy-momentum tensor. The most general such theory respecting the universality of gravitational coupling contains an arbitrary function of the scalar field defining the “observable metric” to which the SM matter is minimally and universally coupled.

In the weak-field slow-motion limit, appropriate to describing gravitational experiments in the solar system, the addition of φ modifies Einstein’s predictions only through the appearance of two dimensionless parameters, γ and β. The best current limits on these “post-Einstein” parameters are, respectively, (2.1±2.3) × 10^–5 (deduced from the additional Doppler shift experienced by radio-wave beams connecting the Earth to the Cassini spacecraft when they passed near the Sun) and < 7 × 10^–5, from a study of the global sensitivity of planetary ephemerides to post-Einstein parameters.

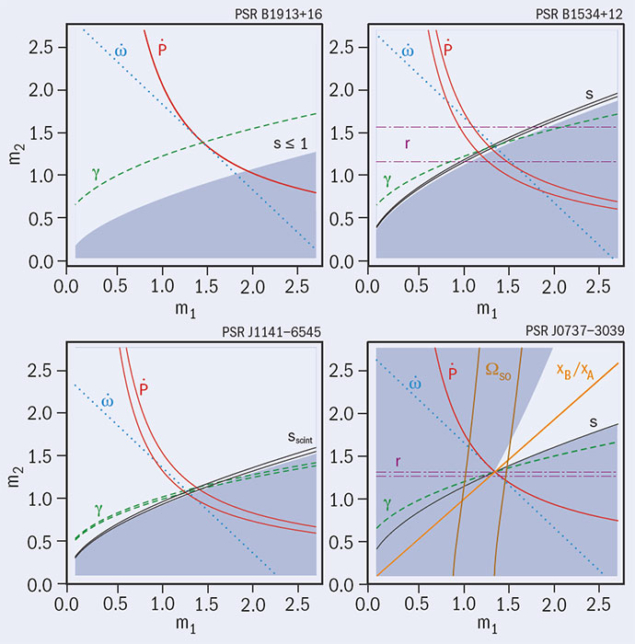
Fig. 2. Illustration of the 11 tests of relativistic gravity obtained in the four known binary pulsar systems. Each curve (or strip) in the mass plane corresponds to the interpretation, within GR, of some observable timing parameter. The shaded regions correspond to s > 1, which is theoretically excluded.

In the regime of radiative and/or strong gravitational fields, by contrast, pulsars (rotating neutron stars emitting a beam of radio waves) in gravitationally bound orbits have provided crucial tests of GR. In particular, measurements of the decay in the orbital period of binary pulsars have provided direct experimental confirmation of the propagation properties of the gravitational field. Theoretical studies of binaries in GR have shown that the finite velocity of propagation of the gravitational interaction between the pulsar and its companion generates damping-like terms at order (v/c)⁵ in the equations of motion that lead to a small orbital period decay. This has been observed in more than four different systems since the discovery of binary pulsars in 1974, providing direct proof of the reality of gravitational radiation. Measurements of the arrival times of pulsar signals have also allowed precision tests of the quasi-stationary strong-field regime of GR, since their values may depend both on the unknown masses of the binary system and on the theory of gravity used to describe the strong self-gravity of the pulsar and its companion (figure 2).

The radiation revelation

Einstein realised that his field equations had wave-like solutions in two papers in June 1916 and January 1918 (see panel below). For many years, however, the emission of gravitational waves (GWs) by known sources was viewed as being too weak to be of physical significance. In addition, several authors – including Einstein himself – had voiced doubts about the existence of GWs in fully nonlinear GR.

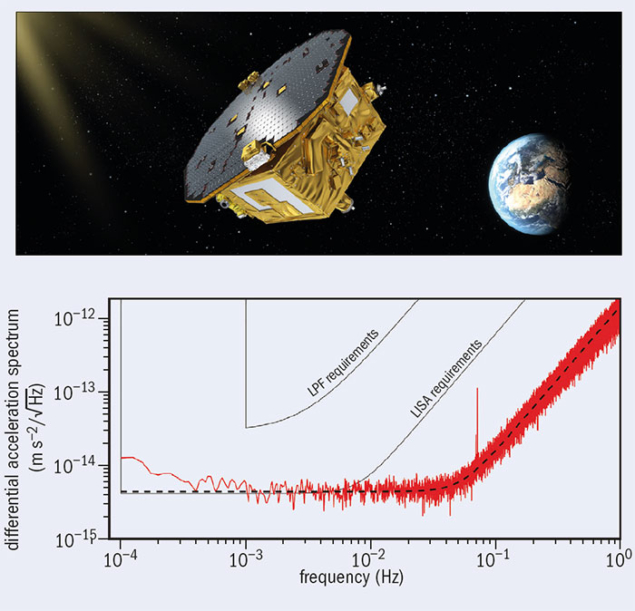
The situation changed in the early 1960s when Joseph Weber understood that GWs arriving on Earth would have observable effects and developed sensitive resonant detectors (“Weber bars”) to search for them. Then, prompted by Weber’s experimental effort, Freeman Dyson realised that, when applying the quadupolar energy-loss formula derived by Einstein to binary systems made of neutron stars, “the loss of energy by gravitational radiation will bring the two stars closer with ever-increasing speed, until in the last second of their lives they plunge together and release a gravitational flash at a frequency of about 200 cycles and of unimaginable intensity.” The vision of Dyson has recently been realised thanks, on the one hand, to the experimental development of drastically more sensitive non-resonant kilometre-scale interferometric detectors and, on the other hand, to theoretical advances that allowed one to predict in advance the accurate shape of the GW signals emitted by coalescing systems of neutron stars and black holes (BHs).

Fig. 3. Simulation of a black-hole merger based on numerical GR.
Image credit: MPI/Simulating eXtreme Spacetimes project.

The recent observations of the LIGO interferometers have provided the first detection of GWs in the wave zone. They also provide the first direct evidence of the existence of BHs via the observation of their merger, followed by an abrupt shut-off of the GW signal, in complete accord with the GR predictions.

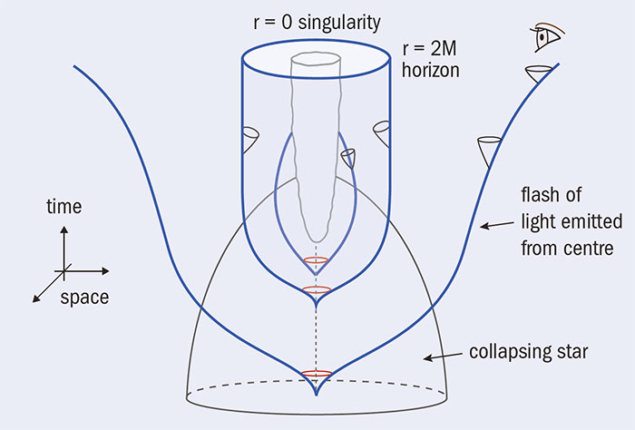
BHs are perhaps the most extraordinary consequence of GR, because of the extreme distortion of space and time that they exhibit. In January 1916, Karl Schwarzschild published the first exact solution of the (vacuum) Einstein equations, supposedly describing the gravitational field of a “mass point” in GR. It took about 50 years to fully grasp the meaning and astrophysical plausibility of these Schwarzschild BHs. Two of the key contributions that led to our current understanding of BHs came from Oppenheimer and Snyder, who in 1939 suggested that a neutron star exceeding its maximum possible mass will undergo gravitational collapse and thereby form a BH, and from Kerr 25 years later, who discovered a generalisation of the Schwarzschild solution describing a BH endowed both with mass and spin.

The Friedmann models still constitute the background models of the current, inhomogeneous cosmologies.

Another remarkable consequence of GR is theoretical cosmology, namely the possibility of describing the kinematics and the dynamics of the whole material universe. The field of relativistic cosmology was ushered in by a 1917 paper by Einstein. Another key contribution was the 1924 paper of Friedmann that described general families of spatially curved, expanding or contracting homogeneous cosmological models. The Friedmann models still constitute the background models of the current, inhomogeneous cosmologies. Quantitative confirmations of GR on cosmological scales have also been obtained, notably through the observation of a variety of gravitational lensing systems.

Dark clouds ahead

In conclusion, all present experimental gravitational data (universality of free fall, post-Newtonian gravity, radiative and strong-field effects in binary pulsars, GW emission by coalescing BHs and gravitational lensing) have been found to be compatible with the predictions of Einstein’s theory. There are also strong constraints on sub-millimetre modifications of Newtonian gravity from torsion-balance tests of the inverse square law.

Fig. 3. (Continued) The gravitational collapse of a star leading to the formation of a BH horizon, a hypersurface in space–time that is everywhere tangent to the light cone and whose 2D spatial sections approach asymptotically (in the future) the r = 2GM/c² 2-sphere of a Schwarzschild solution.

One might, however, wish to keep in mind the presence of two dark clouds in our current cosmology, namely the need to assume that most of the stress-energy tensor that has to be put on the right-hand side of the GR field equations to account for the current observations is made of yet unseen types of matter: dark matter and a “cosmological constant”. It has been suggested that these signal a breakdown of Einstein’s gravitation at large scales, although no convincing theoretical modification of GR at large distances has yet been put forward.

GWs, BHs and dynamical cosmological models have become essential elements of our description of the macroscopic universe. The recent and bright beginning of GW astronomy suggests that GR will be an essential tool for discovering new aspects of the universe (see “The dawn of a new era”). A century after its inception, GR has established itself as the standard theoretical description of gravity, with applications ranging from the Global Positioning System and the dynamics of the solar system, to the realm of galaxies and the primordial universe.

However, in addition to the “dark clouds” of dark matter and energy, GR also poses some theoretical challenges. There are both classical challenges (notably the formation of space-like singularities inside BHs), and quantum ones (namely the non-renormalisability of quantum gravity – see “Gravity’s quantum side”). It is probable that a full resolution of these challenges will be reached only through a suitable extension of GR, and possibly through its unification with the current “spin ≤ 1” description of particle physics, as suggested both by supergravity and by superstring theory.

It is therefore vital that we continue to submit GR to experimental tests of increasing precision. The foundational stone of GR, the equivalence principle, is currently being probed in space at the 10^–15 level by the MICROSCOPE satellite mission of ONERA and CNES. The observation of a deviation of the universality of free fall would imply that Einstein’s purely geometrical description of gravity needs to be completed by including new long-range fields coupled to bulk matter. Such an experimental clue would be most valuable to indicate the road towards a more encompassing physical theory.

General relativity makes waves

There are two equivalent ways of characterising general relativity (GR). One describes gravity as a universal deformation of the Minkowski metric, which defines a local squared interval between two infinitesimally close space–time points and, consequently, the infinitesimal light cones describing the local propagation of massless particles. The metric field g_μν is assumed in GR to be universally and minimally coupled to all the particles of the Standard Model (SM), and to satisfy Einstein’s field equations:

Here, R_μν denotes the Ricci curvature (a nonlinear combination of g_μν and of its first and second derivatives), T_μν is the stress-energy tensor of the SM particles (and fields), and G denotes Newton’s gravitational constant.

The second way of defining GR, as proven by Richard Feynman, Steven Weinberg, Stanley Deser and others, states that it is the unique, consistent, local, special-relativistic theory of a massless spin-2 field. It is then found that the couplings of the spin-2 field to the SM matter are necessarily equivalent to a universal coupling to a “deformed” space–time metric, and that the propagation and self-couplings of the spin-2 field are necessarily described by Einstein’s equations.

Following the example of Maxwell, who had found that the electromagnetic-field equations admit propagating waves as solutions, Einstein found that the GR field equations admit propagating gravitational waves (GWs). He did so by considering the weak-field limit (g_μν = η_μν+ h_μν) of his equations, namely,

where h_μν = h_μν– ½h η_μν. When choosing the co-ordinate system so as to satisfy the gravitational analogue of the Lorenz gauge condition, so that

the linearised field equations simplify to the diagonal inhomogeneous wave equation, which can be solved by retarded potentials.

There are two main results that derive from this wave equation: first, a GW is locally described by a plane wave with two transverse tensorial polarisations (corresponding to the two helicity states of the massless spin-2 graviton) and travelling at the velocity of light; second, a slowly moving, non self-gravitating source predominantly emits a quadupolar GW.

Gravity’s quantum side

A slice through the root space of the symmetry group E10, a possible symmetry for quantum gravity. Each point is associated with one or more independent symmetry operations – similar to the flavour SU(3) root diagram for the meson octet, but vastly more complicated. There are infinitely many such layers, and the number of symmetry operations grows exponentially as one penetrates deeper and deeper into the E10 Lie algebra.
Image credit: T Nutma.

There is little doubt that, in spite of their overwhelming success in describing phenomena over a vast range of distances, general relativity (GR) and the Standard Model (SM) of particle physics are incomplete theories. Concerning the SM, the problem is often cast in terms of the remaining open issues in particle physics, such as its failure to account for the origin of the matter–antimatter asymmetry or the nature of dark matter. But the real problem with the SM is theoretical: it is not clear whether it makes sense at all as a theory beyond perturbation theory, and these doubts extend to the whole framework of quantum field theory (QFT) (with perturbation theory as the main tool to extract quantitative predictions). The occurrence of “ultraviolet” (UV) divergences in Feynman diagrams, and the need for an elaborate mathematical procedure called renormalisation to remove these inﬁnities and make testable predictions order-by-order in perturbation theory, strongly point to the necessity of some other and more complete theory of elementary particles.

On the GR side, we are faced with a similar dilemma. Like the SM, GR works extremely well in its domain of applicability and has so far passed all experimental tests with ﬂying colours, most recently and impressively with the direct detection of gravitational waves (see “General relativity at 100”). Nevertheless, the need for a theory beyond Einstein is plainly evident from the existence of space–time singularities such as those occurring inside black holes or at the moment of the Big Bang. Such singularities are an unavoidable consequence of Einstein’s equations, and the failure of GR to provide an answer calls into question the very conceptual foundations of the theory.

Unlike quantum theory, which is rooted in probability and uncertainty, GR is based on notions of smoothness and geometry and is therefore subject to classical determinism. Near a space–time singularity, however, the description of space–time as a continuum is expected to break down. Likewise, the assumption that elementary particles are point-like, a cornerstone of QFT and the reason for the occurrence of ultraviolet inﬁnities in the SM, is expected to fail in such extreme circumstances. Applying conventional particle-physics wisdom to Einstein’s theory by quantising small ﬂuctuations of the metric ﬁeld (corresponding to gravitational waves) cannot help either, since it produces non-renormalisable inﬁnities that undermine the predictive power of perturbatively quantised GR.

In the face of these problems, there is a wide consensus that the outstanding problems of both the SM and GR can only be overcome by a more complete and deeper theory: a theory of quantum gravity (QG) that possibly unifies gravity with the other fundamental interactions in nature. But how are we to approach this challenge?

Planck-scale physics

Unlike with quantum mechanics, whose development was driven by the need to explain observed phenomena such as the existence of spectral lines in atomic physics, nature gives us very few hints of where to look for QG effects. One main obstacle is the sheer smallness of the Planck length, of the order 10⁻³³ cm, which is the scale at which QG effects are expected to become visible (conversely, in terms of energy, the relevant scale is 10¹⁹ GeV, which is 15 orders of magnitude greater than the energy range accessible to the LHC). There is no hope of ever directly measuring genuine QG effects in the laboratory: with zillions of gravitons in even the weakest burst of gravitational waves, realising the gravitational analogue of the photoelectric effect will forever remain a dream.

If quantum space is made of web-like structures (spin networks), as postulated by LQG-like approaches, a spin foam describes the quantum evolution of such spin networks in time. In the abstract description, the ambient space–time in which the spin foam is “embedded” is simply not there, since all of the geometry resides on the spin foam.

One can nevertheless speculate that QG might manifest itself indirectly, for instance via measurable features in the cosmic microwave background, or cumulative effects originating from a more granular or “foamy” space–time. Alternatively, perhaps a framework will emerge that provides a compelling explanation for inﬂation, dark energy and the origin of the universe. Although not completely hopeless, available proposals typically do not allow one to unambiguously discriminate between very different approaches, for instance when contrarian schemes like string theory and loop quantum gravity vie to explain features of the early universe. And even if evidence for new effects was found in, say, cosmic-ray physics, these might very well admit conventional explanations.

In the search for a consistent theory of QG, it therefore seems that we have no other choice but to try to emulate Einstein’s epochal feat of creating a new theory out of purely theoretical considerations.

Emulating Einstein

Yet, after more than 40 years of unprecedented collective intellectual effort, different points of view have given rise to a growing diversiﬁcation of approaches to QG – with no convergence in sight. It seems that theoretical physics has arrived at crossroads, with nature remaining tight-lipped about what comes after Einstein and the SM. There is currently no evidence whatsoever for any of the numerous QG schemes that have been proposed – no signs of low-energy supersymmetry, large extra dimensions or “stringy” excitations have been seen at the LHC so far. The situation is no better for approaches that do not even attempt to make predictions that could be tested at the LHC.

Existing approaches to QG fall roughly into two categories, reflecting a basic schism that has developed in the community. One is based on the assumption that Einstein’s theory can stand on its own feet, even when confronted with quantum mechanics. This would imply that QG is nothing more than the non-perturbative quantisation of Einstein’s theory and that GR, suitably treated and eventually complemented by the SM, correctly describes the physical degrees of freedom also at the very smallest distances. The earliest incarnation of this approach goes back to the pioneering work of John Wheeler and Bryce DeWitt in the early 1960s, who derived a GR analogue of the Schrödinger equation in which the “wave function of the universe” encodes the entire information about the universe as a quantum system. Alas, the non-renormalisable infinities resurface in a different guise: the Wheeler–DeWitt equation is so ill-deﬁned mathematically that no one until now has been able to make sense of it beyond mere heuristics. More recent variants of this approach in the framework of loop quantum gravity (LQG), spin foams and group field theory replace the space–time metric by new variables (Ashtekar variables, or holonomies and fluxes) in a renewed attempt to overcome the mathematical difficulties.

The opposite attitude is that GR is only an effective low-energy theory arising from a more fundamental Planck-scale theory, whose basic degrees of freedom are very different from GR or quantum field theory. In this view, GR and space–time itself are assumed to be emergent, much like macroscopic physics emerges from the quantum world of atoms and molecules. The perceived need to replace Einstein’s theory by some other and more fundamental theory, having led to the development of supersymmetry and supergravity, is the basic hypothesis underlying superstring theory (see “The many lives of supergravity”). Superstring theory is the leading contender for a perturbatively finite theory of QG, and widely considered the most promising possible pathway from QG to SM physics. This approach has spawned a hugely varied set of activities and produced many important ideas. Most notable among these, the AdS/CFT correspondence posits that the physics that takes place in some volume can be fully encoded in the surface bounding that volume, as for a hologram, and consequently that QG in the bulk should be equivalent to a pure quantum field theory on its boundary.

Apart from numerous technical and conceptual issues, there remain major questions for all approaches to QG. For LQG-like or “canonical” approaches, the main unsolved problems concern the emergence of classical space–time and the Einstein field equations in the semiclassical limit, and their inability to recover standard QFT results such as anomalies. On the other side, a main shortcoming is the “background dependence” of the quantisation procedure, for which both supergravity and string theory have to rely on perturbative expansions about some given space–time background geometry. In fact, in its presently known form, string theory cannot even be formulated without reference to a speciﬁc space–time background.

These fundamentally different viewpoints also offer different perspectives on how to address the non-renormalisability of Einstein’s theory, and consequently on the need (or not) for uniﬁcation. Supergravity and superstring theory try to eliminate the inﬁnities of the perturbatively quantised theory, in particular by including fermionic matter in Einstein’s theory, thus providing a raison d’être for the existence of matter in the world. They therefore automatically arrive at some kind of uniﬁcation of gravity, space–time and matter. By contrast, canonical approaches attribute the ultraviolet inﬁnities to basic deﬁciencies of the perturbative treatment. However, to reconcile this view with semiclassical gravity, they will have to invoke some mechanism – a version of Weinberg’s asymptotic safety – to save the theory from the abyss of non-renormalisability.

Conceptual challenges

Beyond the mathematical difficulties to formulating QG, there are a host of issues of a more conceptual nature that are shared by all approaches. Perhaps the most important concerns the very ground rules of quantum mechanics: even if we could properly deﬁne and solve the Wheeler–DeWitt equation, how are we to interpret the resulting wave function of the universe? After all, the latter pretends to describe the universe in its entirety, but in the absence of outside classical observers, the Copenhagen interpretation of quantum mechanics clearly becomes untenable. On a slightly less grand scale, there are also unresolved issues related to the possible loss of information in connection with the Hawking evaporation of black holes.

A further question that any theory of QG must eventually answer concerns the texture of space–time at the Planck scale: do there exist “space–time atoms” or, more speciﬁcally, web-like structures like spin networks and spin foams, as claimed by LQG-like approaches? (see diagram) Or does the space–time continuum get dissolved into a gas of strings and branes, as suggested by some variants of string theory, or emerge from holographic entanglement, as advocated by AdS/CFT aﬁcionados? There is certainly no lack of enticing ideas, but without a ﬁrm guiding principle and the prospect of making a falsiﬁable prediction, such speculations may well end up in the nirvana of undecidable propositions and untestable expectations.

The success of symmetry has fuelled hopes that we might ultimately understand the evolution of the universe from its beginning as a symmetry-breaking cascade, where at each step more and more of the initial symmetry is lost as the universe expands and cools down. In this view, the unsymmetrical world that we see around us is only the broken phase of a highly symmetrical theory at the origin of the universe, when forces, matter and space–time were uniﬁed into a single entity. However, this picture has so far been validated only up to energy scales accessible to the LHC, or equivalently distances down to 10⁻¹⁸ cm.

Why then consider uniﬁcation? Perhaps the strongest argument in favour of uniﬁcation is that the underlying principle of symmetry has so far guided the development of modern physics from Maxwell’s theory to GR all the way to Yang–Mills theories and the SM (see diagram). It is therefore reasonable to suppose that uniﬁcation and symmetry may also point the way to a consistent theory of QG. This point of view is reinforced by the fact that the SM, although only a partially uniﬁed theory, does already afford glimpses of trans-Planckian physics, independently of whether new physics shows up at the LHC or not. This is because the requirements of renormalisability and vanishing gauge anomalies put very strong constraints on the particle content of the SM, which are indeed in perfect agreement with what we see in detectors. There would be no more convincing vindication of a theory of QG than its ability to predict the matter content of the world (see panel below).

In search of SUSY

Among the promising ideas that have emerged over the past decades, arguably the most beautiful and far reaching is supersymmetry. It represents a new type of symmetry that relates bosons and fermions, thus unifying forces (mediated by vector bosons) with matter (quarks and leptons), and which endows space–time with extra fermionic dimensions. Supersymmetry is very natural from the point of view of cancelling divergences because bosons and fermions generally contribute with opposite signs to loop diagrams. This aspect means that low-energy (N = 1) supersymmetry can stabilise the electroweak scale with regard to the Planck scale, thereby alleviating the so-called hierarchy problem via the cancellation of quadratic divergences. These models predict the existence of a mirror world of superpartners that differ from the SM particles only by their opposite statistics (and their mass), but otherwise have identical internal quantum numbers.

To the great disappointment of many, experimental searches at the LHC so far have found no evidence for the superpartners predicted by N = 1 supersymmetry. However, there is no reason to give up on the idea of supersymmetry as such, since the refutation of low-energy supersymmetry would only mean that the most simple-minded way of implementing this idea does not work. Indeed, the initial excitement about supersymmetry in the 1970s had nothing to do with the hierarchy problem, but rather because it offered a way to circumvent the so-called Coleman–Mandula no-go theorem – a beautiful possibility that is precisely not realised by the models currently being tested at the LHC.

In fact, the reduplication of internal quantum numbers predicted by N = 1 supersymmetry is avoided in theories with extended (N > 1) supersymmetry. Among all supersymmetric theories, maximal N = 8 supergravity stands out as the most symmetric. Its status with regard to perturbative finiteness is still unclear, although recent work has revealed amazing and unexpected cancellations. However, there is one very strange agreement between this theory and observation, first emphasised by Gell-Mann: the number of spin-1/2 fermions remaining after complete breaking of supersymmetry is 48 = 3 × 16, equal to the number of quarks and leptons (including right-handed neutrinos) in three generations (see “The many lives of supergravity”). To go beyond the partial matching of quantum numbers achieved so far will, however, require some completely new insights, especially concerning the emergence of chiral gauge interactions.

Then again, perhaps supersymmetry is not the end of the story. There is plenty of evidence that another type of symmetry may be equally important, namely duality symmetry. The ﬁrst example of such a symmetry, electromagnetic duality, was discovered by Dirac in 1931. He realised that Maxwell’s equations in vacuum are invariant under rotations of the electric and magnetic ﬁelds into one another – an insight that led him to predict the existence of magnetic monopoles. While magnetic monopoles have not been seen, duality symmetries have turned out to be ubiquitous in supergravity and string theory, and they also reveal a fascinating and unsuspected link with the so-called exceptional Lie groups.

More recently, hints of an enormous symmetry enhancement have also appeared in a completely different place, namely the study of cosmological solutions of Einstein’s equations near a space-like singularity. This mathematical analysis has revealed tantalising evidence of a truly exceptional inﬁnite-dimensional duality symmetry, which goes by the name of E10, and which “opens up” as one gets close to the cosmological (Big Bang) singularity (see image at top). Could it be that the near-singularity limit can tell us about the underlying symmetries of QG in a similar way as the high-energy limit of gauge theories informs us about the symmetries of the SM? One can validly argue that this huge and monstrously complex symmetry knows everything about maximal supersymmetry and the ﬁnite-dimensional dualities identiﬁed so far. Equally important, and unlike conventional supersymmetry, E10 may continue to make sense in the Planck regime where conventional notions of space and time are expected to break down. For this reason, duality symmetry could even supersede supersymmetry as a unifying principle.

Outstanding questions

Our summary, then, is very simple: all of the important questions in QG remain wide open, despite a great deal of effort and numerous promising ideas. In the light of this conclusion, the LHC will continue to play a crucial role in advancing our understanding of how everything ﬁts together, no matter what the ﬁnal outcome of the experiments will be. This is especially true if nature chooses not to abide by current theoretical preferences and expectations.

Over the past decades, we have learnt that the SM is a most economical and tightly knit structure, and there is now mounting evidence that minor modifications may suffice for it to survive to the highest energies. To look for such subtle deviations will therefore be a main task for the LHC in the years ahead. If our view of the Planck scale remains unobstructed by intermediate scales, the popular model-builders’ strategy of adding ever more unseen particles and couplings may come to an end. In that case, the challenge of explaining the structure of the low-energy world from a Planck-scale theory of quantum gravity looms larger than ever.

Einstein on unification

An extract from Einstein’s 1929 paper in which he set out his approach to unification. (From a contribution to a commemorative publication for Aurel Stodola, Zurich, 1929.)

It is well known that Albert Einstein spent much of the latter part of his life vainly searching for uniﬁcation, although disregarding the nuclear forces and certainly with no intention of reconciling quantum mechanics and GR. Already in 1929, he published a paper on the uniﬁed theory (pictured above right, click to enlarge). In this paper, he states with wonderful and characteristic lucidity what the criteria should be of a “good” uniﬁed theory: to describe as far as possible all phenomena and their inherent links, and to do so on the basis of a minimal number of assumptions and logically independent basic concepts. The second of these goals (also known as the principle of Occam’s razor) refers to “logical unity”, and goes on to say: “Roughly but truthfully, one might say: we not only want to understand how nature works, but we are also after the perhaps utopian and presumptuous goal of understanding why nature is the way it is and not otherwise.”

The LHC’s extra dimension

The presence of a large extra dimension could produce a clear missing-energy signal in the LHC detectors, as shown here for an ATLAS event recorded in 2011 with a missing transverse energy of 523 GeV.

At 10.00 a.m. on 9 August 2016, physicists gathered at the Sheraton hotel in Chicago for the “Beyond the Standard Model” session at the ICHEP conference. The mood was one of slight disappointment. An excess of “diphoton” events at a mass of 750 GeV reported by the LHC’s ATLAS and CMS experiments in 2015 had not shown up in the 2016 data, ending a burst of activity that saw some 540 phenomenology papers uploaded to the arXiv preprint server in a period of just eight months. Among the proposed explanations for the putative new high-mass resonance were extra space–time dimensions, an idea that has been around since Theodor Kaluza and Oscar Klein attempted to unify the electromagnetic and gravitational forces a century ago.

In the modern language of string theory, extra dimensions are required to ensure the mathematical consistency of the theory. They are typically thought to be very small, close to the Planck length (10^–35 m). In the 1990s, however, theorists trying to solve problems with supersymmetry suggested that some of these extra dimensions could be as large as 10^–19 m, corresponding to an energy scale in the TeV range. In 1998, as proposed by Arkani-Hamed and co-workers, theories emerged with even larger extra dimensions, which predicted detectable effects in contemporary collider experiments. In such large extra-dimension (LED) scenarios, gravity can become stronger than we perceive in 3D due to the increased space available. In addition to showing us an entirely different view of the universe, extra dimensions offer an elegant solution to the so-called hierarchy problem, which arises because the Planck scale (where gravity becomes as strong as the other three forces) is 17 orders of magnitude larger than the electroweak scale.

Particle physicists normally ignore gravity because it is feeble compared with the other three forces. In theories where gravity gets stronger at small distances due to the opening of extra dimensions, however, it can catch up and lead to phenomena at colliders with high enough rates that they can be measured in experiments. The possibility of having extra space dimensions at the TeV scale was a game changer. Scientists from experiments at the LEP, Tevatron and HERA colliders quickly produced tailored searches for signals for this new beyond-the-Standard Model (SM) physics scenario. No evidence was found in their accumulated data, setting lower limits on the scale of extra dimensions of around 1 TeV.

Fig. 1. Recent mono-jet searches at ATLAS have pushed possible extra-dimension scales to values beyond 5–7 TeV, depending on the number of assumed large extra dimensions available for gravity to expand into.

By the turn of the century, a number of possible new experimental signatures had been identified for extra-dimension searches, many of which were studied in detail while assessing the physics performance of the LHC experiments. For the case of LEDs, where gravity is the only force that can expand in these dimensions, high-energy collider experiments were just one approach. Smaller “tabletop” scale experiments aiming to measure the strength of gravity at sub-millimetre distances were also in pursuit of extra dimensions, but no deviation from the Newtonian law has been observed to date. In addition, there were also significant constraints from astrophysics processes on the possible number and size of these dimensions.

Enter the LHC

Analysis strategies to search for extra dimensions have been deployed from the beginning of high-energy LHC operations in 2010, and the recent increase in the LHC’s collision energy to 13 TeV has extended the search window considerably. Although no positive signal of the presence of extra dimensions has been observed so far, a big leap forward has been taken in excluding large portions of the TeV scale phase-space where extra dimensions could live.

A particular feature of LED-type searches is the production of a single very energetic “mono-object” that does not balance the transverse momentum carried by anything else emerging from the collision (as would be required by momentum and energy conservation). Examples of such objects are particle jets, very energetic photons or heavy W and Z vector bosons. Such collisions only appear to be imbalanced, however, because the emerging jet or boson is balanced by a graviton that escapes detection. Hence SM processes such as the production of a jet plus a Z boson that decays into neutrinos can mimic a graviton production signal. The absence of any excess in the mono-jet or mono-photon event channels at the LHC has put stringent limits on LEDs (figure 1), with 2010 data already bypassing previous collider search limits. LEDs can also manifest themselves as a new contribution to the continuum in the invariant mass spectrum of two energetic photons (figure 2) or fermions (dileptons or dijets). Here too, though, no signals have been observed, and the LHC has now excluded such contributions for extra-dimension scales up to several TeV.

Fig. 2. Observed event yields and background expectations as a function of the diphoton invariant mass for an early extra-dimension study at the LHC. The simulated distributions for two extra-dimension model signal hypotheses are shown as dotted (LED) and dashed (RS) lines.

In 1999, another extra-dimension scenario was proposed by Randall and Sundrum (RS), which led to a quite different phenomenology compared with that expected from LEDs. In its simplest form, the RS idea contains two fundamental 3D branes: one on which most if not all SM particles live, and one on which gravity lives. Gravity is assumed to be intrinsically strong, but the warped space between the two branes makes it appear weak on the brane where we live. The experimental signature of such scenarios is the production of so-called Kaluza–Klein (spin-2 graviton) resonances that can be observed in the invariant mass spectra of difermions or dibosons. The most accessible spectra to the LHC experiments include the diphoton and dilepton spectra, in which no new resonance signal has been found, and at present the limits on putative Kaluza–Klein gravitons are about 4 TeV, depending on RS-model parameters. Analyses of dijet final states provide even more stringent limits of up to 7 TeV. Further extensions of the RS model, in particular the production of top quark–antiquark resonances, offer a more sensitive signature, but despite intense searches, no signal has been detected.

Searching in the dark

At the start of 2000, it was realised that large or warped extra dimensions could lead to a new type of signature at the LHC: microscopic black holes. These can form when two colliding partons come close enough to each other, namely to within the Schwarzschild radius or black-hole event horizon, and can be as large as a femtometre in the presence of TeV-scale extra dimensions at the LHC. Such microscopic black holes would evaporate via Hawking radiation on time scales of around 10^–27 s, way before they could suck up any matter, and provide an ideal opportunity to study quantum gravity in the laboratory.

Black holes that are produced with a mass significantly above the formation threshold are expected to evaporate in high-energy multi-particle final states leading to plenty of particle jets, leptons, photons and even Higgs particles. Searches for such energetic multi-object final states in excess of the SM expectation have been performed since the first collisions at the LHC at 7 TeV, but none have been found. If black holes are produced closer to the formation threshold, these would be expected to decay in a much smaller final-state topology, for instance into dijets. The CMS and ATLAS experiments have been looking for all of these final states up until the latest 13 TeV data (figure 3), but no signal has been observed so far for black-hole masses up to about 9 TeV.

Fig. 3. Distributions of the total transverse energy for events with eight high-p_T objects. Observed data are shown by points, while the solid blue lines show the main background estimation along with the uncertainty band. The predictions for several semiclassical black-hole signals are also shown.

Several other possible incarnations of extra-dimension theories have been proposed and searched for at the LHC. So-called TeV-type extra dimensions allow for more SM particles, for example partners of the heavy W and Z bosons, to enter in the bulk, and these would show up as high-mass resonances in dilepton and other invariant mass spectra. These new resonances have a spin equal to one, and hence such signatures could be more tedious to detect because they can interfere with the SM Drell–Yan production background. Nevertheless, no such resonances have been discovered so far.

In so-called universal extra-dimension (UED) scenarios, all particles have states that can go into the bulk. If this scenario is correct, a completely new particle spectrum of partners of the SM particles should show up at the LHC at high masses. Although this looks very much like what would be expected from supersymmetry, where all known SM particles have partners, the Kaluza–Klein partners would have exactly the same spin as their SM partners, whereas supersymmetry transforms bosons into fermions and vice versa. Alas, no new particles either for Kaluza–Klein partners or supersymmetry candidates have been observed, pushing the lower mass limits beyond 1 TeV for certain particle types.

Final hope

Collider data so far have not yet given us any sign of the existence of extra dimensions, or for that matter a sign that gravity is becoming strong at the TeV scale. It is possible that, even if they exist, the extra dimensions could be as small as predicted by string theory, in which case they would not be able to solve the hierarchy problem. The idea is still very much alive, however, and searches will continue as more data are recorded at the LHC.

Even excellent and attractive ideas always need confirmation from data, and inevitably the initial high enthusiasm for extra-dimension theories may have waned somewhat in recent years. Although such confirmation could come from the next generation of colliders, such as possible higher-energy machines, there is unfortunately no guarantee. It could be that we have to turn to even more outlandish ideas to progress further.

Catching a gravitational wave

Aerial view of the Hanford (Washington state) LIGO site. Clearly visible are the two 4 km arms stretching across the desert to the end mirror stations. The surface “tunnels” use sections of reinforced concrete U-profiles covering the 1.2 m diameter vacuum pipes.

Gravitational waves alternatively compress and stretch space–time as they propagate, exerting tidal forces on all objects in their path. Detectors such as Advanced LIGO (aLIGO) search for this subtle distortion of space–time by measuring the relative separation of mirrors at the ends of long perpendicular arms, which form a simple Michelson interferometer with Fabry–Perot cavities in the arms: a beam splitter directs laser light to mirrors at the ends of the arms and the reflected light is recombined to produce an interference pattern. When a gravitational wave passes through the detector, the strain it exerts changes the relative lengths of the arms and causes the interference pattern to change.

The arms of the aLIGO detectors are each 4 km long to help maximise the measured length change. Even on this scale, however, the induced length changes are tiny: the first detected gravitational waves, from the merger of two black holes, changed the arm length of the aLIGO detectors by just 4 × 10^–18 m, which is approximately 200 times smaller than the proton radius. Achieving the fantastically high sensitivity required to detect this event was the culmination of decades of research and development.

Battling noise

The idea of using an interferometer to detect gravitational waves was first concretely proposed in the 1970s and full-scale detectors began to be constructed in the mid-1990s, including GEO600 in Germany, Virgo in Italy and the LIGO project in the US. LIGO consists of detectors at two sites separated by about 3000 km – Hanford (in Washington state) and Livingston in Louisiana – and undertook its first science runs in 2002–2008. Following a major upgrade, the observatory restarted in September 2015 as aLIGO with an initial sensitivity four times greater than its predecessor. Since the detectors measure strain in space–time, the effective increase in volume, or event rate, of aLIGO is a factor 4³ higher.

A major issue facing aLIGO designers is to isolate the detectors from various noise sources. At a frequency of around 10 Hz, the motion of the Earth’s surface or seismic noise is about 10 orders of magnitude larger than required, with the seismic noise falling off at higher frequencies. A powerful solution is to suspend the mirrors as pendulums: a pendulum acts as a low-pass filter, providing significant reductions in motion at frequencies above the pendulum frequency. In aLIGO, a chain of four suspended masses is used to provide a factor 10⁷ reduction in seismic motion. In addition, the entire suspension is attached to an advanced seismic isolation system using a variety of active and passive techniques, which further isolate noise by a factor 1000. At 10 Hz, and in the absence of other noise sources, these systems could already increase the sensitivity of the detectors to roughly 10^–19 m/√(Hz). At even lower frequencies (10 μHz), the daily tides stretch and shrink the Earth by the order of 0.4 mm over 4 km.

Another source of low-frequency noise arises from moving mass interacting with the detector mirrors via the Newtonian inverse square law. The dominant source of this noise is from surface seismic waves, which can produce density fluctuations of the Earth’s surface close to the interferometer mirrors and result in a fluctuating gravitational force on them. While methods of monitoring and subtracting this noise are being investigated, the performance of Earth-based detectors is likely to always be limited at frequencies below 1 Hz by this noise source.

The design sensitivity of aLIGO, showing the dominant noise sources.
Image creditL LIGO Lab.

Thermal noise associated with the thermal energy of the mirrors and their suspensions can also cause the mirrors to move, providing a significant noise source at low-to-mid-range frequencies. The magnitude of thermal noise is related to the mechanical loss of the materials: similar to a high-quality wine glass, a material with a low loss will ring for a long time with a pure note because most of the thermal motion is confined to frequencies close to the resonance. For this reason, aLIGO uses fibres fabricated from fused silica – a type of very pure glass with very low mechanical loss – for the final stage of the mirror suspension. Pioneered in the GEO600 detector near Hanover in Germany, the use of silica fibres in place of the steel wires used in the initial LIGO detectors significantly reduces thermal noise from suspension.

aLIGO also has much reduced quantum noise compared with the original LIGO.

Low-loss fused silica is also used for the 40 kg interferometer mirrors, which use multi-layered optical coatings to achieve the high reflectivity required. For aLIGO, a new optical coating was developed comprising a stack of alternating layers of silica and titania-doped “tantala”, reducing the coating thermal noise by about 20%. However, at the aLIGO design sensitivity (which is roughly 10 times higher than the initial aLIGO set-up) thermal noise will be the limiting noise source at frequencies of around 60 Hz – close to the frequency at which the detectors are most sensitive.

aLIGO also has much reduced quantum noise compared with the original LIGO. This noise source has two components: radiation-pressure noise and shot noise. The former results from fluctuations in the number of photons hitting the detector mirrors, which is more significant at lower frequencies, and has been reduced by using mirrors four times heavier than the initial LIGO mirrors. Photon shot noise, resulting from statistical fluctuations in the number of photons at the output of the detector, limits sensitivity at higher frequencies. Since shot noise is inversely proportional to the square root of the power, it can be reduced by using higher laser power. In the first observing run of aLIGO, 100 kW of laser power was circulating in the detector arms, with the potential to increase it to up to 750 kW in future runs. Optical cavities are also used to store light in the arms and build up laser power.

In addition to reductions in these fundamental noise sources, many other technological improvements were required to reduce more technical noise sources. Improvements over the initial LIGO detector included a thermal compensation system to reduce thermal lensing effects in the optics, reduced electronic noise in control circuits and finer polishing of the mirror substrates to reduce the amount of scattered light in the detectors.

Upgrades on the ground

Having detected their first gravitational wave almost as soon as they switched on in September 2015, followed by a further event a few months later, the aLIGO detectors began their second observation run on 30 November. Dubbed “O2”, it is scheduled to last for six months. More observation runs are envisaged, with more upgrades in sensitivity taking place between them.

aLIGO uses a chain of four suspended masses to provide a factor 107 reduction in seismic motion. To achieve this level of shielding, each of aLIGO’s 40 kg test masses is suspended within a 360 kg quadruple pendulum system.
Image credits: LIGO Lab.

The next major upgrade, expected in around 2018, will see the injection of “squeezed light” to further reduce quantum noise. However, to gain the maximum sensitivity improvement from squeezing, a reduction in coating thermal noise is also likely to be required. With these and other relatively short-term upgrades, it is expected that a factor-two improvement over the aLIGO design sensitivity could be achieved. This would allow events such as the first detection to be observed with a signal-to-noise ratio almost 10 times better than the initial result. Further improvements in sensitivity will almost certainly require more extensive upgrades or new facilities, possibly involving longer detectors or cryogenic cooling of the mirrors.

aLIGO is expected to soon be joined in observing runs by Advanced Virgo, giving a network of three geographically separated detectors and thus improving our ability to locate the position of gravitational-wave sources on the sky. Discussions are also under way for an aLIGO site in India. In Japan, the KAGRA detector is under construction: this detector will use cryogenic cooling to reduce thermal noise and is located underground to reduce seismic and gravity gradient effects. When complete, KAGRA is expected to have similar sensitivity to aLIGO.

Longer term, in Europe a detector known as the Einstein Telescope (ET) has been proposed to provide a factor 10 more sensitivity than aLIGO. ET would not only have arms measuring 10 km long but would take a new approach to noise reduction using two very different detectors: a high-power room-temperature interferometer optimised for sensitivity at high frequencies, where shot noise limits performance, and a low-power cryogenic interferometer optimised for sensitivity at low frequencies (where performance is limited by thermal noise). ET would require significant changes in detector technology and also be constructed underground to reduce the effect of seismic noise and gravity-gradient noise on low-frequency sensitivity.

The final frontier

Obtaining significantly improved sensitivity at lower frequencies is difficult on Earth because they are swamped by local mass motion. Gaining sensitivity at very low frequencies, which is where we must look for signals from massive black-hole collisions and other sources that will provide exquisite science results, is only likely to be achieved in space. This concept has been on the table since the 1970s and has evolved into the Laser Interferometer Space Antenna (LISA) project, which is led by the European Space Agency (ESA) with contributions from 14 European countries and the US.

Initial results from LISA Pathfinder show that the technology is close to meeting requirements for a full gravitational-wave detector in space (*Phys. Rev. Lett.* **116** 231101). At frequencies above 60 mHz, its precision is only limited by the sensing noise of the laser measurement system, while at lower frequencies of 1–60 mHz, control over the test masses is limited by the residual (and decreasing) small number of gas molecules bouncing off them. Frequencies below 1 mHz exhibit noise as a result of keeping the craft’s solar panels pointing towards the Sun, most of which is removable.

A survey mission called LISA Pathfinder was launched on 3 December 2015 from French Guiana. It is currently located 1.5 million km away at the first Earth–Sun Lagrange point, and will take data until the end of May 2017. The aim of LISA Pathfinder was to demonstrate technologies for a space-borne gravitational-wave detector based on the same measurement philosophy as that used by ground-based detectors. The mission has clearly demonstrated that we can place test masses (gold–platinum cubes with 46 mm sides separated by 38 cm) into free fall, such that the only varying force acting on them is gravity. It has also validated a host of complementary techniques, including: operating a drag-free spacecraft using cold gas thrusters; electrostatic control of free-floating test masses; short-arm interferometry and test-mass charge control. When combined, these novel features allow differential accelerometry at the 10^–15 g level, which is the sensitivity needed for a space-borne gravitational-wave detector. Indeed, if Pathfinder test-mass technology were used to build a full-scale LISA detector, it would recover almost all of the science originally anticipated for LISA without any further improvements.

The success of Pathfinder, coming hot on the heels of the detection of gravitational waves, is a major boost for the international gravitational-wave community. It comes at an exceptional time for the field, with ESA currently inviting proposals for the third of its Cosmic Vision “large missions” programme. Developments are now needed to move from LISA Pathfinder to LISA proper, but these are now well understood and technology development programmes are planned and under way. The timeline for this mission leads to a launch in the early 2030s and the success of Pathfinder means we can look forward with excitement to the fantastic science that will result.

Does antimatter fall up?

The AEgIS flight tube from which atoms of antihydrogen will be fired to test if antimatter falls under gravity the same way matter does.
Image credit: M Doser.

Measuring the effect of gravity on antimatter is a long-standing story. It started with a project at Stanford in 1968 that attempted to measure the free fall of positrons, but a trial experiment with electrons showed that environmental effects swamped the effect of gravity and the final experiment was not performed. In the 1990s, the PS200 experiment at CERN’s LEAR facility attempted the same feat with antiprotons, but the project ended with the termination of LEAR before any robust measurement could be made. To date, indirect measurements have set limits on the deviation from standard gravity at the level of 10^–6.

Thanks to advances in cooling and trapping technology, and the construction of a new synchrotron at CERN called ELENA, three collaborations are now preparing experiments at CERN’s Antiproton Decelerator (AD) facility to measure the behaviour of antihydrogen (a positron orbiting an antiproton) under gravity. The ALPHA experiment has already analysed its data on the trapping of antihydrogen atoms to set upper limits on differences in the free-fall rate of matter and antimatter, and is now designing a new set-up. AEgIS is currently putting its apparatus through its paces, while GBAR will start installation in 2017.

Given that most of the mass of antinuclei comes from massless gluons, it is extremely unlikely that antimatter experiences an opposite gravitational force to matter and therefore “falls” up. Nevertheless, precise measurements of the free fall of antiatoms could reveal subtle differences that point to a crack in our current understanding.

Violating equivalence

To date, most efforts at the AD have focused on looking for CPT violation by comparing the spectroscopy of antihydrogen to its well-known matter counterpart, hydrogen. Now we are in a position to test Einstein’s equivalence principle with antimatter by directly measuring the free fall of antiatoms on Earth. The equivalence principle is the keystone of general relativity and states that all particles with the same initial position and velocity should follow the same trajectories in a given gravitational field. On the other hand, quantum theories such as supersymmetry or superstrings do not necessarily lead to an equivalent force on matter and antimatter (technically, the terms related to gravity in the Lagrangians are not bound to be the same for matter and antimatter). This is also the case when Lorentz-symmetry violating terms are included in the Standard Model of particle physics.

Any difference seen in the behaviour of antimatter and matter with respect to gravity would mean that the equivalence principle is not perfect and force us to understand quantum effects in the gravitational arena. Experiments performed with free-falling matter atoms have so far found no difference to that of macroscopic objects. Such tests have set limits at the level of one part in 10¹³, but have not yet been able to test the equivalence principle at the level where supersymmetric or other quantum effects would appear. Since the amplitude of these effects could be different for antimatter, the AD experiments might have a better opportunity to test such quantum effects. Any difference would probably not change anything in the observable universe, but it would point to the necessity of having a quantum theory of gravity.

The production of antihydrogen in AEgIS (left) and GBAR (right) is performed via the interaction of antiprotons with positronium (Ps). In AEgIS, a plasma of antiprotons at rest in a Penning trap is showered with excited positronium atoms, producing excited antihydrogen atoms that are accelerated to form a beam. In GBAR, a dense positronium cloud is traversed by a beam of antiprotons to produce antihydrogen atoms and ions.

AEgIS plans to measure the vertical deviation of a pulsed horizontal beam of cold antihydrogen atoms, generated by bringing laser-excited positronium moving at several km/s into contact with cold antiprotons, travelling with a velocity of a few hundred m/s. The resulting highly excited antihydrogen atoms are then accelerated horizontally and a moiré deflectometer used to measure the vertical deviation, which is expected to be a few microns given the approximately 1 m-long flight tube of AEgIS. Reaching the lowest possible antiproton temperature minimises the divergence of the beam and therefore maximises the flux of antihydrogen atoms that end up on the downstream detector.

In GBAR, which takes advantage of advances in ion-cooling techniques, antihydrogen ions (H⁺) are produced with velocities of the order of 0.5 m/s. In a second step, the anti-ions will be stripped of one positron to give an ultra-slow neutral antiatom that is allowed to enter free fall. The time of free fall over a height of 20 cm is as long as 200 ms, which is easily measurable. These numbers correspond to the gravitational acceleration known for matter atoms, and the expected sensitivity to small deviations is 1% in the first phase of operation.

The ALPHA-g experiment will release antihydrogen atoms from a vertical magnetic atom trap and record their positions when they annihilate on the walls of the experiment. In a proof-of-principle experiment using the original ALPHA atom trap, the acceleration of antihydrogen atoms by gravity was constrained to lie anywhere between –110 g and 65 g. ALPHA-g improves on this original demonstration by orienting the trap vertically, thereby enabling better control of the antiatom release and improving sensitivity to the vertical annihilation position. In the new arrangement, antihydrogen gravitation can be measured at the 10% level, which would already settle the question of whether antimatter falls up or down, but improvements in cooling techniques will allow measurements at the 1% level. A long-term aspiration of the ALPHA-g project is to use techniques that cause antihydrogen atoms to interact with a beam of photons, promising a sensitivity in the 10^–6 range.

Cooling matter

In the case of AEgIS, the deflectometer principle that underpins the measurement has already been demonstrated with matter atoms and with antiprotons, while the time-of-flight measurement is straightforward in the case of GBAR. The difficulty for the experiments lies in preparing sufficient numbers of antiatoms at the required low velocities. ALPHA has already demonstrated trapping of several hundred antiatoms at a temperature below 0.5 K, corresponding to random velocities of the order 10 m/s. The antiatoms are formed by letting the antiprotons traverse a plasma of positrons located within the same Penning trap.

A different scheme is used in AEgIS and GBAR to form and possibly cool the antiatoms and anti-ions. In AEgIS, antiprotons are cooled within a Penning trap and receive a shower of positronium atoms (bound e⁺e^– pairs) to form the antiatoms. These are then slightly accelerated by electric fields (which act on the atoms’ induced electric-dipole moments) so that they exit the charged particle trap axially in the form of a neutral beam. For GBAR, the antiproton beam traverses a cloud of positronium to form the anti-ions, which are then cooled to a few μK by forcing them to interact with laser-cooled beryllium ions.

In this race towards low energies, ALPHA and AEgIS are located on the beam at the AD, which delivers 5 MeV antiprotons. While AEgIS is already commissioning its dedicated gravity experiment, ALPHA will move from spectroscopy to gravity in the coming months. GBAR, which will be the first experiment to make use of the beam delivered by ELENA, is now beginning installation and expects first attempts at anti-ion production in 2018. ELENA will decelerate antiprotons coming from the AD from 5 MeV to just 100 keV, making it more efficient to trap and store antimatter. Following commissioning first with protons and then with hydrogen ions, ELENA should receive its first antiprotons in the middle of 2017 (CERN Courier December 2016 p16). Along with precision tests of CPT invariance, this facility will help to ensure that any differences in the gravitational antics of antimatter are not missed.

The many lives of supergravity

The early 1970s was a pivotal period in the history of particle physics. Following the discovery of asymptotic freedom and the Brout–Englert–Higgs mechanism a few years earlier, it was the time when the Standard Model (SM) of electroweak and strong interactions came into being. After decades of empirical verification, the theory received a final spectacular confirmation with the discovery of the Higgs boson at CERN in 2012, and its formulation has also been recognised by Nobel prizes awarded to theoretical physics in 1979, 1999, 2004 and 2013.

It was clear from the start, however, that the SM, a spontaneously broken gauge theory, had two major shortcomings. First, it is not a truly unified theory because the gluons of the strong (colour) force and the photons of electromagnetism do not emerge from a common symmetry. Second, it leaves aside gravity, the other fundamental force of nature, which is based on the gauge principle of general co-ordinate transformations and is described by general relativity (GR).

In the early 1970s, grand unified theories (GUTs), based on larger gauge symmetries that include the SM’s “SU(3) × SU(2) × U(1)” structure, did unify colour and charge – thereby uniting the strong and electroweak interactions. However, they relied on a huge new energy scale (~10¹⁶ GeV), just a few orders of magnitude below the Planck scale of gravity (~10¹⁹ GeV) and far above the electroweak Fermi scale (~10² GeV), and on new particles carrying both colour and electroweak charges. As a result, GUTs made the stunning prediction that the proton might decay at detectable rates, which was eventually excluded by underground experiments, and their two widely separated cut-off scales introduced a “hierarchy problem” that called for some kind of stabilisation mechanism.

A possible solution came from a parallel but unrelated development. In 1973, Julius Wess and Bruno Zumino unveiled a new symmetry of 4D quantum field theory: supersymmetry, which interchanges bosons and fermions and, as would be better appreciated later, can also conspire to stabilise scale hierarchies. Supersymmetry was inspired by “dual resonance models”, an early version of string theory pioneered by Gabriele Veneziano and extended by André Neveu, Pierre Ramond and John Schwarz. Earlier work done in France by Jean-Loup Gervais and Benji Sakita, and in the Soviet Union by Yuri Golfand and Evgeny Likhtman, and by Dmitry Volkov and Vladimir Akulov, had anticipated some of supersymmetry’s salient features.

Participants of the first workshop on supergravity, held at Stony Brook in September 1979. (From P Van Nieuwenhuizen and D Freedman ed 1979 *Supergravity. Proceedings, Workshop At Stony Brook, 27–29 September 1979* (North-Holland).)

An exact supersymmetry would require the existence of superpartners in the SM, but it would also imply mass degeneracies between the known particles and their superpartners. This option has been ruled out over the years by several experiments at CERN, Fermilab and elsewhere, and therefore supersymmetry can be at best broken, with superpartner masses that seem to lie beyond the TeV energy region currently explored at the LHC. Moreover, a spontaneous breaking of supersymmetry would imply the existence of additional massless (“Goldstone”) fermions.

Supergravity, the supersymmetric extension of GR, came to the rescue in this respect. It predicted the existence of a new particle of spin 3/2 called the gravitino that would receive a mass in the broken phase. In this fashion, one or more gravitinos could be potentially very heavy, while the additional massless fermions would be “eaten” – much as it occurs for part of the Higgs doublet in the SM.

Seeking unification

Supergravity, especially when formulated in higher dimensions, was the first concrete realisation of Einstein’s dream of a unified field theory (see diagram opposite). Although the unification of gravity with other forces was the central theme for Einstein during the last part of his life, the beautiful equations of GR were for him a source of frustration. For 30 years he was disturbed by what he considered a deep flaw: one side of the equations contained the curvature of space–time, which he regarded as “marble”, while the other contained the matter energy, which he compared to “wood”. In retrospect, Einstein wanted to turn “wood” into “marble”, but after special and general relativity he failed in this third great endeavour.

GR has, however, proved to be an inestimable source of deep insights for unification. A close scrutiny of general co-ordinate transformations led Theodor Kaluza and Oskar Klein (KK), in the 1920s and 1930s, to link electromagnetism and its Maxwell potentials to internal circle rotations, what we now call a U(1) gauge symmetry. In retrospect, more general rotations could also have led to the Yang–Mills theory, which is a pillar of the SM. According to KK, Maxwell’s theory could be a mere byproduct of gravity, provided the universe contains one microscopic extra dimension beyond time and the three observable spatial ones. In this 5D picture, the photon arises from a portion of the metric tensor – the “marble” in GR – with one “leg” along space–time and the other along the extra dimensions.

Current attempts to unify the fundamental interactions.

Supergravity follows in this tradition: the gravitino is the gauge field of supersymmetry, just like the photon is the gauge field of internal circle rotations. If one or more local supersymmetries (whose number will be denoted by N) accompany general co-ordinate transformations, they grant the consistency of gravitino interactions. In a subclass of “pure” supergravity models, supersymmetry also allows one to connect “marble” and “wood” and therefore goes well beyond the KK mechanism, which does not link Bose and Fermi fields. Curiously, while GR can be formulated in any number of dimensions, seven additional spatial dimensions, at most, are allowed in supergravity due to intricacies of the Fermi–Bose matching.

Last year marked the 40th anniversary of the discovery of supergravity. At its heart lie some of the most beautiful ideas in theoretical physics, and therefore over the years this theory has managed to display different facets or has lived different parallel lives.

Construction begins

The first instance of supergravity, containing a single gravitino (N = 1), was built in the spring of 1976 by Daniel Freedman, Peter van Nieuwenhuizen and one of us (SF). Shortly afterwards, the result was recovered by Stanley Deser and Bruno Zumino, in a simpler and elegant way that extended the first-order (“Palatini”) formalism of GR. Further simplifications emerged once the significance of local supersymmetry was better appreciated. Meanwhile, the “spinning string” – the descendant of dual resonance models that we have already met – was connected to space–time supersymmetry via the so-called Gliozzi–Scherk–Olive (GSO) projection, which reflects a subtle interplay between spin-statistics and strings in space–time. The low-energy spectrum of the resulting models pointed to previously unknown 10D versions of supergravity, which would include the counterparts of several gravitinos, and also to a 4D Yang–Mills theory that is invariant under four distinct supersymmetries (N = 4). A first extended (N = 2) version of 4D supergravity involving two gravitinos came to light shortly after.

When SF visited Caltech in the autumn of 1976, he became aware that Murray Gell-Mann had already worked out many consequences of supersymmetry. In particular, Gell-Mann had realised that the largest “pure” 4D supergravity theory, in which all forces would be connected to the conventional graviton, would include eight gravitinos. Moreover, this N = 8 theory could also allow an SO(8) gauge symmetry, the rotation group in eight dimensions (see table opposite). Although SO(8) would not suffice to accommodate the SU(3) × SU(2) × U(1) symmetry group of the SM, the full interplay between supergravity and supersymmetric matter soon found a proper setting in string theory, as we shall see.

The following years, 1977 and 1978, were most productive and drew many people into the field. Important developments followed readily, including the discovery of reformulations where N = 1 4D supersymmetry is manifest. This technical step was vital to simplify more general constructions involving matter, since only this minimal form of supersymmetry is directly compatible with the chiral (parity-violating) interactions of the SM. Indeed, by the early 1980s, theorists managed to construct complete couplings of supergravity to matter for N = 1 and even for N = 2.

The particles of “pure” supergravity theories in four dimensions, which coincide for N = 7, 8. Here (0) indicates a scalar, (1/2) a Majorana fermion, (1) a vector, (3/2) a gravitino and (2) the graviton. The numbers not within brackets indicate particle multiplicities.

The maximal, pure N = 8 4D supergravity was also derived, via a circle KK reduction, in 1978 by Eugene Cremmer and Bernard Julia. This followed their remarkable construction, with Joel Scherk, of the unique 11D form of supergravity, which displayed a particularly simple structure where a single gravitino accounts for eight 4D ones. In contrast, the N = 8 model is a theory of unprecedented complication. It was built after an inspired guess about the interactions of its 70 scalar fields (see table) and a judicious use of generalised dualities, which extend the manifest symmetry of the Maxwell equations under the interchange of electric and magnetic fields. The N = 8 supergravity with SO(8) gauge symmetry foreseen by Gell-Mann was then constructed by Bernard de Wit and Hermann Nicolai. It revealed a negative vacuum energy, and thus an anti-de Sitter (AdS) vacuum, and was later connected to 11D supergravity via a sphere KK reduction. Regarding the ultraviolet behaviour of supergravity theories, which was vigorously investigated soon after the original discovery, no divergences were found, at one loop, in the “pure” models, and many more unexpected cancellations of divergences have since come to light. The case of N = 8 supergravity is still unsettled, and some authors still expect that this maximal theory be finite to all orders.

The string revolution

Following the discovery of supergravity, the GSO projection opened the way to connect “spinning strings”, or string theory as they came to be known collectively, to supersymmetry. Although the link between strings and gravity had been foreseen by Scherk and Schwarz, and independently by Tamiaki Yoneya, it was only a decade later, in 1984, that widespread activity in this direction began. This followed Schwarz and Michael Green’s unexpected discovery that gauge and gravitational anomalies cancel in all versions of 10D supersymmetric string theory. Anomalies – quantum violations of classical symmetries – are very troublesome when they concern gauge interactions, and their cancellation is a fundamental consistency condition that is automatically granted in the SM by its known particle content.

Anomaly cancellation left just five possible versions of string theory in 10 dimensions: two “heterotic” theories of closed strings, where the SU(3) × SU(2) × U(1) symmetry of the SM is extended to the larger groups SO(32) or E8 × E8; an SO(32) “type-I” theory involving both open and closed strings, akin to segments and circles, respectively; and two other very different and naively less interesting theories called IIA and IIB. At low energies, supergravity emerges from all of these theories in its different 10D realisations, opening up unprecedented avenues for linking 10D strings to the interactions of particle physics. Moreover, the extended nature of strings made all of these enticing scenarios free of the ultraviolet problems of gravity.

Following this 1984 “first superstring revolution”, one might well say that supergravity officially started a second life as a low-energy manifestation of string theory. Anomaly cancellation had somehow connected Einstein’s “marble” and “wood” in a miraculous way dictated by quantum consistency, and definite KK scenarios soon emerged that could recover from string theory both the SM gauge group and its chiral, parity-violating interactions. Remarkably, this construction relied on a specific class of 6D internal manifolds called Calabi–Yau spaces that had been widely studied in mathematics, thereby merging 4D supergravity with algebraic geometry. Calabi–Yau spaces led naturally, in four dimensions, to a GUT gauge group E6, which was known to connect to the SM with right-handed neutrinos, also providing realisations of the see-saw mechanism.

A third life

The early 1990s were marked by many investigations of black-hole-like solutions in supergravity, which soon unveiled new aspects of string theory. Just like the Maxwell field is related to point particles, some of the fields in 10D supergravity are related to extended objects, generically dubbed “p-branes” (p = 0 for particles, p = 1 for strings, p = 2 for membranes, and so on). String theory, being based at low energies on supergravity, therefore could not be merely a theory of strings. Rather, as had been strongly advocated over the years by Michael Duff and Paul Townsend, we face a far more complicated soup of strings and more general p-branes. A novel ingredient was a special class of p-branes, the D-branes, whose role was clarified by Joseph Polchinski, but the electric-magnetic dualities of the low-energy supergravity remained the key tool to analyse the system. The end result, in the mid 1990s, was the awesome, if still somewhat vague, unified picture called M-theory, which was largely due to Edward Witten and marked the “second superstring revolution”. Twenty years after its inception, supergravity thus started a third parallel life, as a deep probe into the mysteries of string theory.

M-theory revealed a unique, if elusive, underlying principle connecting the known types of string theory, since the six theories at the edges of the diagram are all equivalent. The sides of the diagram reflect different duality links. Some were inspired by supergravity, while the others had already surfaced in the late 1980s. They are beyond its reach but find their rationale in the “T-duality” link between strings in large and small KK volumes, and in the “orientifold” link proposed by one of us (AS).

The late 1990s witnessed the emergence of a new duality. The AdS/CFT correspondence, pioneered by Juan Maldacena, is a profound equivalence between supergravity and strings in AdS and conformal field theory (CFT) on its boundary, which connects theories living in different dimensions. This “third superstring revolution” brought to the forefront the AdS versions of supergravity, which thus started a new life as a unique tool to probe quantum field theory in unusual regimes. The last two decades have witnessed many applications of AdS/CFT outside of its original realm. These have touched upon fluid dynamics, quark–gluon plasma, and more recently condensed-matter physics, providing a number of useful insights on strongly coupled matter systems. Perhaps more unexpectedly, AdS/CFT duality has stimulated work related to scattering amplitudes, which may also shed light on the old issue of the ultraviolet behaviour of supergravity. The reverse programme of gaining information about gravity from gauge dynamics has proved harder, and it is difficult to foresee where the next insights will come from. Above all, there is a pressing need to highlight the geometrical principles and the deep symmetries underlying string theory, which have proved elusive over the years.

The interplay between particle physics and cosmology is a natural arena to explore consequences of supergravity. Recent experiments probing the cosmic microwave background, and in particular the results of the Planck mission, lend support to inflationary models of the early universe. An elusive particle, the inflaton, could have driven this primordial acceleration, and although our current grasp of string theory does not allow a detailed analysis of the problem, supergravity can provide fundamental clues on this and the subsequent particle-physics epochs.

Supersymmetry was inevitably broken in a de Sitter-like inflationary phase, where superpartners of the inflaton tend to experience instabilities. The novel ingredient that appears to get around these problems is non-linear supersymmetry, whose foundations lie in the prescient 1973 work of Volkov and Akulov. Non-linear supersymmetry arises when superpartners are exceedingly massive, and seems to play an intriguing role in string theory. The current lack of signals for supersymmetry at the LHC makes one wonder whether it might also hold a prominent place in an eventual picture of particle physics. This resonates with the idea of “split supersymmetry”, which allows for large mass splittings among superpartners and can be accommodated in supergravity at the price of reconsidering hierarchy issues.

In conclusion, attaining a deeper theoretical understanding of broken supersymmetry in supergravity appears crucial today. In breaking supersymmetry, one is confronted with important conceptual challenges: the resulting vacua are deeply affected by quantum fluctuations, and this reverberates on old conundrums related to dark energy and the cosmological constant. There are even signs that this type of investigation could shed light on the backbone of string theory, and supergravity may also have something to say about dark matter, which might be accounted for by gravitinos or other light superpartners. We are confident that supergravity will lead us farther once more.

Linking waves to particles

Gravitational waves could provide a link between strong gravity (left) and particle physics (right).

Black holes are arguably humankind’s most intriguing intellectual construction. Featuring a curvature singularity where space–time “ends” and tidal forces are infinite, black-hole interiors cannot be properly understood without a quantum theory of gravity. They are defined by an event horizon – a surface beyond which nothing escapes to the outside – and an exterior region called a photosphere, which is able to trap light rays. These uncommon properties explain why black holes were basically ignored for half a century, considered little more than a bizarre mathematical solution of Einstein’s equations but one without counterpart in nature.

LIGO’s discovery of gravitational waves provides the strongest evidence to date for the existence of black holes, but these tiny distortions of space–time have much more to tell us. Gravitational waves offer a unique way to test the basic tenets of general relativity, some of which have been taken for granted without observations. Are black holes the simplest possible macroscopic objects? Do event horizons and black holes really exist, or is their formation halted by some as-yet unknown mechanism? In addition, gravitational waves can tell us if gravitons are massless and if extra-light degrees of freedom fill the universe, as predicted in the 1970s by Peccei and Quinn in an attempt to explain the smallness of the neutron electric-dipole moment, and more recently by string theory. Ultralight fields affect the evolution of black holes and their gravitational-wave emission in a dramatic way that should be testable with upcoming gravitational-wave observatories.

The existence of black holes

The standard criterion with which to identify a black hole is straightforward: if an object is dark, massive and compact, it’s a black hole. But are there other objects which could satisfy the same criteria? Ordinary stars are bright, while neutron stars have at most three solar masses and therefore neither is able to explain observations of very massive dark objects. In recent years, however, unknown physics and quantum effects in particular have been invoked that change the structure of the horizon, replacing it by a hard surface. In this scenario, the exterior region – including the photosphere – would remain unchanged, but black holes would be replaced by very compact, dark stars. These stars could be made of normal matter under extraordinary quantum conditions or of exotic matter such as new scalar particles that may form “boson stars”.

Unfortunately, the formation of objects invoking poorly understood quantum effects is difficult to study. The collapse of scalar fields, on the other hand, can theoretically allow boson stars to form, and these may become more compact and massive through mergers. Interestingly, there is mounting evidence that compact objects without horizons but with a photosphere are unstable, ruling out entire classes of alternatives that have been put forward.

Fig. 1. Typical gravitational-wave signal generated by a small star falling into a massive compact object with (top) and without (bottom) a horizon. In the latter case, “echoes” of gravitational waves appear at late time and provide a smoking gun for putative quantum effects that halt the gravitational collapse.

Gravitational waves might soon provide a definite answer to such questions. Although current gravitational-wave detections are not proof for the existence of black holes, they are a strong indicator that photospheres exist. Whereas observations of electromagnetic processes in the vicinities of black holes only probe the region outside of the photosphere, gravitational waves are sensitive to the entire space–time and are our best probe of strong-field regions.

A typical gravitational-wave signal generated by a small star falling head-on into a massive black hole looks like that in figure 1. As the star crosses the photosphere, a burst of radiation is emitted and a sequence of pulses dubbed “quasinormal ringing” follow, determined by the characteristic modes of the black hole. But if the star falls into a quantum-corrected or exotic compact object with no horizon, part of the burst generated during the crossing of the photosphere reflects back at the object surface. The resulting signal in a detector would thus initially look the same, but be followed by lower amplitude “echoes” trapped between the photosphere and the surface of the object (figure 1, lower panel). These echoes, although tricky to dig out in noisy data, would be a smoking gun for new physics. With increasing sensitivity in detectors such as LIGO and Virgo, observations will be pushing back the object’s surface closer to the horizon, perhaps even to the point where we can detect the echo of quantum effects.

Dark questions

Understanding strong-field gravity with gravitational waves can also test the nature of dark matter. Although dark matter may interact very feebly with Standard Model particles, according to Einstein’s equivalence principle it must fall just like any other particle. If dark matter is composed of ultralight fields, as recent studies argue, then black holes may serve as excellent dark-matter detectors. You might ask how a monstrous, supermassive black hole could ever be sensitive to ultralight fields. The answer lies in superradiant resonances. When black holes rotate, as most do, they display an interesting effect discovered in the 1970s called superradiance: if one shines a low-frequency lamp on a rotating black hole, the scattered beam is brighter. This happens at the expense of the hole’s kinetic energy, causing the spin of the black-hole to decrease.

Fig. 2. Exclusion plots in the black-hole mass-spin plane for ultralight scalar (top), vector (middle) and tensor (bottom) fields, showing electromagnetic (black) and gravitational-wave (red) observations. Above each curve (grey), superradiance would spin the black hole down to the threshold, whereas below the curve accretion is dominant and there is no spin-down effect.

Not only electromagnetic waves, but also gravitational waves and any other bosonic field can be amplified by a rotating black hole. In addition, if the field is massive, low-energy fluctuations are trapped near the horizon and are forced to interact repeatedly with the black hole, producing an instability. This instability extracts rotational energy and transfers it to the field, which grows exponentially in amplitude and forms a rotating cloud around the black hole. For a one-million solar-mass black hole and a scalar field with a mass of 10^–16 eV, the timescale for this to take place is less than two minutes. Therefore, the very existence of ultralight fields is constrained by the observation of spinning black holes. With this technique, one can place unprecedented bounds on the mass of axion-like particles, another popular candidate for dark matter. For example, we know from current astrophysical observations that the mass of dark photons must be smaller than 10^–20 eV, which is 100 times better than accelerator bounds. The technique relies only on measurements of the mass and spin of black holes, which will be known with unprecedented precision with future gravitational-wave observations.

Superradiance, together with current electromagnetic observations of spinning black holes, can also be used to constrain the mass of the graviton, since any massive boson would trigger superradiant instabilities. Spin measurements of the supermassive black hole in galaxy Fairall 9 requires the mass of the graviton to be lighter than 5 × 10^–23 eV – an impressive number which is even more stringent than the bound recently placed by LIGO.

Gravitational lighthouses

Furthermore, numerical simulations suggest that the superradiant instability mechanism eventually causes a slowly evolving and non-symmetric cloud to form around the black hole, emitting periodic gravitational waves like a gravitational “lighthouse”. This would not only mean that black holes are not as simple as we thought, but lead to a definite prediction: some black holes should be emitting nearly monochromatic gravitational waves whose frequency is dictated only by the field’s mass. This raises terrific opportunities for gravitational-wave science: not only can gravitational waves provide the first direct evidence of ultralight fields and of possible new effects near the horizon, but they also carry detailed information about the black-hole mass and spin. If light fields exist, the observation of a few hundred black holes should show “gaps” in the mass-spin plane corresponding to regions where spinning black holes are too unstable to exist.

This is a surprising application of gravitational science, which can be used to investigate the existence of new particles such as those possibly contributing to the dark matter. The idea of using observations of supermassive black holes to provide new insights not accessible in laboratory experiments would certainly be exciting. Perhaps these new frontiers in gravitational-wave astrophysics, in addition to probing the most extreme objects, will also give us a clearer understanding of the microscopic universe.

Unity through global science

CERN’s geographical enlargement policy of 2010 has been turned into a strategy to help secure the long-term future of particle physics. Image credit: M Brice/CERN.

CERN’s Large Hadron Collider (LHC) and its discovery of the Higgs boson in 2012 have launched a new era of research in particle physics. The LHC and its upgrades will chart the course of the field for many years to come, and CERN is therefore in a unique position to help shape the long-term future of particle physics. In view of this, CERN is exploring two different and challenging projects: the Compact Linear Collider (CLIC) and a Future Circular Collider (FCC).

These developments are taking place at a time when facilities for high-energy physics, as for other branches of science, are becoming larger and more complex as well as requiring more resources. Funding for the field is not increasing in many countries and the timescale for projects is becoming longer, resulting in fewer facilities being realised. Particle physics must adapt to this evolving reality by fostering greater co-ordination and collaboration on a global scale. This goes hand in hand with CERN’s tradition of networking with worldwide partners.

In 2010, CERN Council approved a radical shift in CERN’s membership policy that opened full membership to non-European states, irrespective of their geographical location. At the same time, Council introduced the status of associate membership to facilitate the accession of new members, including countries outside of Europe that might not command sufficient resources to sustain full membership (CERN Courier December 2014 p58).

Geographical enlargement is part of the effort to secure the future of the laboratory, and the process has been gradual and measured. Israel became CERN’s 21st Member State in 2014 while Romania joined as the 22nd Member State in 2016. Cyprus and Serbia are presently associate members in the pre-stage to membership, while Pakistan, Turkey and Ukraine are associate members. Late last year, agreements with Slovenia for associate membership in the pre-stage to membership and with India for associate membership were signed (see “Slovenia to become associate Member State in pre-stage to membership” and “India to become associate Member State” in this issue). Brazil, Croatia, Lithuania and Russia have also applied for associate membership.

CERN builds on a long tradition of a global engagement. The Organization has formal relations with non-member states (NMS) via bilateral International Co-operation Agreements (ICAs), currently in force with 47 countries. Out of a total of about 12,700 users at CERN, the participation of NMS users is now almost 40% – the majority of which are researchers from the US and Russia working on the LHC. The overall NMS participation in the non-LHC research programme is currently about 20%. Financial resources for research programmes, notably maintenance and operation costs for the LHC experiments, are shared between the Member States, the associate members and the NMS. In addition, there is increasing interest in collaboration on accelerator R&D and related technologies, focusing on the LHC’s luminosity upgrades and also on the FCC and CLIC studies. The number of states involved in such activities is already growing beyond the restricted circle of NMS that contributed to the LHC accelerator construction. The increasingly global interest in CERN also translates into a rising demand for CERN’s education and training programmes – falling within CERN’s mission of helping build capacity in countries that are developing their particle-physics communities.

The geographical enlargement policy of 2010 offers important opportunities for the future of the Organization. Now, CERN has developed it into a strategy, presented to Council in March 2016, to ensure that geographical enlargement consolidates the institutional base and thus reinforces the long-term scientific aspirations of CERN. Enlargement is not an aim in and of itself. Rather, the focus is on strengthening relations with countries that can bring scientific and technological expertise to CERN and can, in turn, benefit from closer engagement.

It is essential that membership and associate membership are beneficial to particle physics in individual countries, and that governments continue to invest in the growth of national communities. At the same time, enlargement should not hinder the operational efficiency of the laboratory. CERN’s engagement with prospective members and associate members is clearly oriented towards these objectives, mindful that investigating the unification of the fundamental forces of nature requires uniting scientific efforts on a global scale.

Raman Spectroscopy: An Intensity Approach

By Wu Guozhen
World Scientific

In this book the author offers an overview of Raman spectroscopy techniques – including Raman optical activity (ROA) and surface-enhanced Raman scattering spectroscopy (SERS) – covering their applications and their theoretical foundations.

The Raman effect is an inelastic two-photon process in which the incident (scattering) photon is absorbed by an atom or molecule (the scatterer) that immediately emits a photon of different energy and frequency than the incident one. This energy difference, which arises because the incident photon vibrationally excites the molecule, is called the Raman shift. Raman shifts provide information on the molecular motion and thus its structure and bond strength. As a consequence, this effect is used for material analysis in Raman spectroscopy.

More important than the energy difference are the Raman intensity of the scattered light, which offers insights into the dynamics of the photon-perturbed molecule, and the electronic polarisability of the molecule, which is a measure of how easily the electrons can be affected by the light.

After introducing the Raman effect and the normal mode analysis, the author discusses the bond polarisabilities, the intensity analysis and the Raman virtual states. A group of chapters then cover the extension of the bond polarisability algorithm to the ROA intensity analysis and many findings on ROA mechanism resulting from the work of the author and his collaborators. The last chapter introduces a unified classical theory for ROA and vibrational circular dichroism (another spectroscopic technique).

Relativistic Density Functional for Nuclear Structure

By Jie Meng (ed.)
World Scientific

This book, the 10th volume of the International Review of Nuclear Physics series, provides an overview of the current status of relativistic density functional theories and their applications. Written by leading scientists in the field, it is intended both for students and for researchers interested in many-body theory or nuclear physics.

Density functional theory was introduced in 1970s and has since developed in an attempt to find a unified and self-consistent description of the single-particle motion in a nucleus and of the collective motions of the nucleus based on strong interaction theory. Largely applied for heavy and super-heavy nuclei, this description allows mapping the complex quantum-mechanical many-body problem of the structure of these nuclei onto an adequate one-body problem, which is relatively easy to solve.

After explaining the theoretical basics of relativistic (or covariant) density functional theory, the authors discuss different models and the application of the theory to various cases, including the structure of neutron stars. In the last chapter, three variants of the relativistic model and the non-relativistic density model are compared. Possible directions for future developments of energy density functional theory are also outlined.

Readers interested in further details and specific research work can rely on the very rich bibliography that accompanies each chapter.

Topics

Reset your password

Registration complete