Extending the elementary-particle inventory with heavy neutral leptons could solve the key observational shortcomings of the Standard Model, explain Alexey Boyarsky and Mikhail Shaposhnikov, with some models placing the new particles in reach of current and proposed experiments.

In the 1960s, the creators of the Standard Model made a smart choice: while all charged fermions came in pairs, with left-handed and right-handed components, neutrinos were only left-handed. This “handicap” of neutrinos allowed physicists to accommodate in the most economical way important features of the experimental data at that time. First, such left-handed-only neutrinos are naturally massless, and second, individual leptonic flavours (electron, muon and tau) are automatically conserved.
It is now well established that neutrinos have masses and that the neutrino flavours mix with each other, in similarity with quarks. If this were known 55 years ago, Weinberg’s seminal 1967 work “A Model of Leptons” would be different: in addition to the left-handed neutrinos, it would very likely also contain their right-handed counterparts. The structure of the Standard Model (SM) dictates that these new states, if they exist, are the only singlets with respect to weak-isospin and hyper-charge gauge symmetry and thus do not participate directly in electroweak interactions (see “On the other hand” figure). This makes right-handed neutrinos (also referred to as sterile neutrinos, singlet fermions or heavy neutral leptons) very special: unlike charged quarks and leptons, which get their masses from the Yukawa interaction with the Brout–Englert–Higgs field, the masses of right-handed neutrinos depend on an additional parameter – the Majorana mass – which is not related to the vacuum expectation value and which results in the violation of lepton-number conservation. As such, right-handed neutrinos are also sometimes referred to as Majorana leptons or Majorana fermions.
Leaving aside the possible signals of eV-scale neutrino states reported in recent years, all established experimental signatures of neutrino oscillations can be explained by the SM with the addition of two heavy-neutral leptons (HNLs). If there were only one HNL, then two out of three SM neutrinos would be massless; with two HNLs, only one of the SM neutrinos is massless – this is not excluded experimentally. Any larger number of HNLs is also possible.

The simplest way to extend the SM in the neutrino sector is to add several HNLs and no other new particles. Already this class of theories is very rich (different numbers of HNLs and different values of their masses and couplings imply very different phenomenology), and contains several different scenarios explaining not only the observed masses and flavour oscillations of the SM neutrinos but also other phenomena that are not accommodated by the SM. The scenario in which the Majorana masses of right-handed neutrinos are much higher than the electroweak scale is known as the “type I see-saw model”, first put forward in the late 1970s. The theory with three right-handed neutrinos (the same as the number of generations in the SM) with their masses below the electroweak scale is called the neutrino minimal standard model (νMSM), and was proposed in the mid-2000s.
Would these new particles be useful for anything else besides neutrino physics? The answer is yes. The first, lightest HNL N1 may serve as a dark-matter particle, whereas the other two HNLs N2,3 not only “give” masses to active neutrinos but can also lead to the matter–antimatter asymmetry of the universe. In other words, the SM extended by just three HNLs could solve the key outstanding observational problems of the SM, provided the masses and couplings of the HNLs are chosen in a specific domain.

The leptonic extension of the SM by right-handed neutrinos is quite similar to the gradual adaptation of electroweak theory to experimental data during the past 50 years. While the bosonic sector of the electroweak model remains intact from 1967, with the discoveries of the W and Z bosons in 1983 and the Higgs boson in 2012, the fermionic sector evolved from one to two to three generations, revealing the remarkable symmetry between quarks and leptons. It took about 20 years to find all the quarks and leptons of the third generation. How much time it will take to discover HNLs, if they indeed exist, depends crucially on their masses.
The value of the Majorana mass, and therefore the physical mass of an HNL, is arbitrary from a theoretical point of view and cannot be found from neutrino-oscillation experiments. The famous see-saw formula that relates the observed masses of the active neutrinos to the Majorana masses of HNLs has a degeneracy: change the Yukawa couplings of HNLs to neutrinos by a factor x and the HNL masses by a factor x2, and the active neutrino masses and the physics of their oscillations remain intact. The scale of HNL masses thus can be any number from a fraction of an eV to 1015 GeV (see “Options abound” figure). Moreover, there could be several HNLs with very different masses. Indeed, even in the SM the masses of charged fermions, though they share a similar origin, differ by almost six orders of magnitude.
Motivated by the value of the active neutrino masses, the HNL could be light, with masses of the order of 1 eV. Alternatively, similar to the known quarks and charged leptons, they could be somewhere around the GeV or Fermi scale. Or they could be close to the grand unification scale, 1015 GeV, where the strong and electromagnetic interactions are thought to be unified. These possibilities have different theoretical and experimental consequences.
The case of the light sterile neutrino
The see-saw formula tells us that if the mass of HNLs is around 1 eV, their Yukawa couplings should be of the order of 10–12. Such light sterile neutrinos can be potentially observed in neutrino experiments, as they can be involved in the oscillations together with the three active neutrino species. Several experiments – including LSND, GALLEX, SAGE, MiniBooNE and BEST – have reported anomalies in neutrino-oscillation data (the so-called short-baseline, gallium and reactor anomalies) that could be interpreted as a signal for the existence of light sterile neutrinos. However, it looks difficult, if not impossible, to reconcile the existence of these states with recent negative results of other experiments such as MINOS+, MicroBooNE and IceCUBE, accounting for additional constraints coming from β-decay, neutrinoless double-β decay and cosmology.
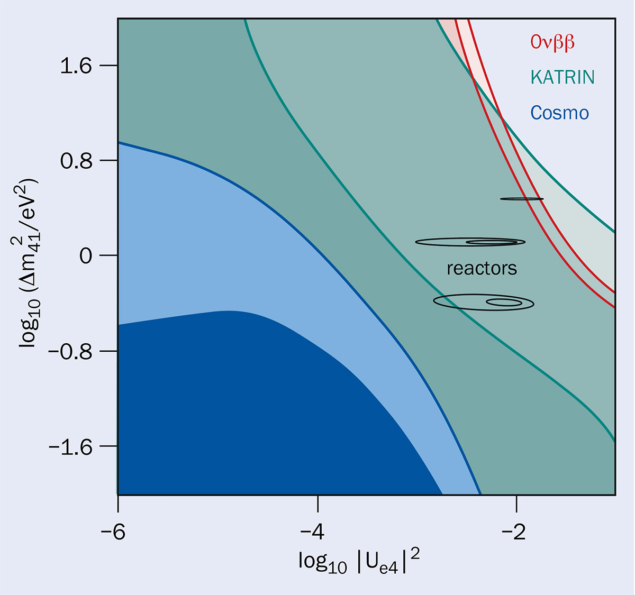
The parameters of light sterile neutrinos required to explain the experimental anomalies are in strong tension with the cosmological bounds (see “Cosmological bounds” figure). For example, their mixing angle with the ordinary neutrinos should be sufficiently large that these states would have been produced abundantly in the early universe, affecting its expansion rate during Big Bang nucleosynthesis and thus changing the abundances of the light elements. In addition, light sterile neutrinos would affect the formation of structure. Having been created in the hot early universe with relativistic velocities, they would have escaped from forming structures until they cooled down in much later epochs. This so-called “hot dark matter” scenario would mean that the smallest structures, which form first, and the larger ones, which require much more time to develop, would experience different amounts of dark matter. Moreover, the presence of such particles would affect baryon acoustic oscillations and therefore impact the value of the Hubble constant deduced from them.
Besides tensions between the experiments and cosmological bounds, light sterile neutrinos do not provide any solution to the outstanding problems of the SM. They cannot be dark-matter particles because they are too light, nor can they produce the baryon asymmetry of the universe as their Yukawa couplings are too small to give any substantial contribution to lepton-number violation at the temperatures (> 160 GeV) at which the anomalous electroweak processes with baryon non-conservation have a chance to convert a lepton asymmetry into a baryon asymmetry.
Three Fermi-scale heavy neutral leptons
Another possible scale for HNL masses is around a GeV, plus or minus a few orders of magnitude. Right-handed neutrinos with such masses do not interfere with active-neutrino oscillations because the corresponding length over which these oscillations may occur is far too small. As only two active-neutrino mass differences are fixed by neutrino-oscillation experiments, it is sufficient to have two HNLs N2,3 with appropriate Yukawa couplings to active neutrinos: to get the correct neutrino masses, they should not be smaller than ~10–8 (compared to the electron Yukawa coupling of ~10–6). These two HNLs may produce the baryon asymmetry of the universe, as we explain later, whereas the lightest singlet fermion, N1, may interact with neutrinos much more weakly and thus can be a dark-matter particle (although unstable, its lifetime can greatly exceed the age of the universe).
Three main considerations determine the possible range of masses and couplings of the dark-matter sterile neutrino (see “Dark-matter constraints” figure). The first is cosmological production. If N1 interact too strongly, they would be overproduced in ℓ+ℓ– → N1ν reactions and make the abundance of dark matter larger than what is inferred by observations, providing an upper limit on their interaction strength. Conversely, the requirement to produce enough dark matter results in a lower bound on the mixing angle that depends on the conditions in the early universe during the epoch of N1 production. Moreover, the lower bound completely disappears if N1 can also be produced at very high temperatures by interactions related to gravity or at the end of cosmological inflation. The second consideration is X-ray data. Radiative N1 → γν decays produce a narrow line that can be detected by X-ray telescopes such as XMM–Newton or Chandra, resulting in an upper limit on the mixing angle between sterile and active neutrinos. While this upper limit depends on the uncertainties in the distribution of dark matter in the Milky Way and other nearby galaxies and clusters, as well as on the modelling of the diffuse X-ray background, it is possible to marginalise these to obtain very robust constraints.

The third consideration for the sterile neutrino’s properties is structure formation. If N1 is too light, a very large number-density of such particles is required to make an observed halo of a small galaxy. As HNLs are fermions, however, their number density cannot exceed that of a completely degenerate Fermi gas, placing a very robust lower bound on the N1 mass. This bound can be further improved by taking into account that light dark-matter particles remain relativistic until late epochs and therefore suppress or erase density perturbations on small scales. As a result, they would affect the inner structure of the halos of the Milky Way and other galaxies, as well as the matter distribution in the intergalactic medium, in ways that can be observed via gravitational-lensed galaxies, gaps in the stellar streams in galaxies and the spectra of distant quasars.
Neutrino experiments and robust conclusions from observational cosmology call for extensions of the SM
The upper limits on the interaction strength of sterile neutrinos fixes the overall scale of active neutrino masses in the νMSM. The dark-matter sterile neutrino effectively decouples from the see-saw formula, making the mass of one of the active neutrinos much smaller than the observed solar and atmospheric neutrino-mass differences and fixing the masses of the two other active neutrinos to approximately 0.009 eV and 0.05 eV (for the normal ordering) and to the near-degenerate value 0.05 eV for the inverted ordering.
HNLs at the GeV scale and beyond
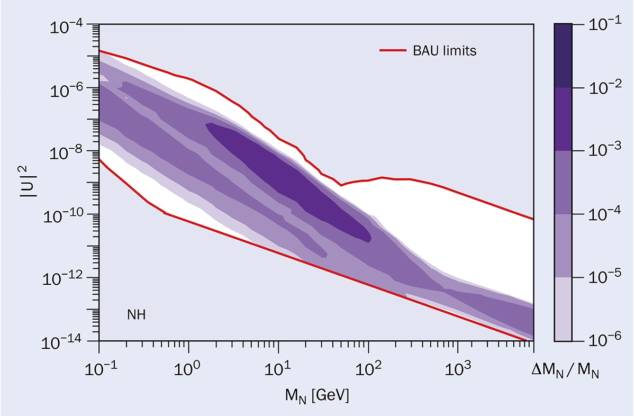
Our universe is baryon-asymmetric – it does not contain antimatter in amounts comparable with the matter. Though the SM satisfies all three “Sakharov conditions” necessary for baryon-asymmetry generation (baryon number non-conservation, C and CP-violation, and departure from thermal equilibrium), it cannot explain the observed baryon asymmetry. The Kobayashi–Maskawa CP-violation is too small to produce any substantial effects, and departures from thermal equilibrium are tiny at the temperatures at which the anomalous fermion-number non-conserving processes are active. This is not the case with two GeV-scale HNLs: these particles are not in thermal equilibrium for temperatures above a few tens of GeV, and CP violation in their interactions with leptons can be large. As a result, a lepton asymmetry is produced, which is converted into baryon asymmetry by the baryon-number violating reactions of the SM.
The requirement to get baryon asymmetry in the νMSM puts stringent constraints on the masses and coupling of HNLs (see “Baryon-asymmetry constraints” figure). The mixing angle of these particles cannot be too large, otherwise they equilibrate and erase the baryon asymmetry, and it cannot be below a certain value because it would make the active neutrino masses too small. We know that their mass should be larger than that of the pion, otherwise their decays in the early universe would break the success of Big Bang nucleosynthesis. In addition, the masses of two HNLs should be close to each other so as to enhance CP-violating effects. Interestingly, the HNLs with these properties are within the experimental reach of existing and future accelerators, as we shall see.
The final possible choice of HNL masses is associated with the grand unification scale, ~1015 GeV. To get the correct neutrino masses, the Yukawa couplings of a pair of these superheavy particles should be of the order of one, in which case the baryon asymmetry of the universe can be produced via thermal leptogenesis and anomalous baryon- and lepton-number non-conservation at high temperatures. The third HNL, if interacting extremely weakly, may play the role of a dark-matter particle, as described previously. Another possibility is that there are three superheavy HNLs and one light one, to play the role of dark matter. This model, as well as that with HNL masses of the order of the electroweak scale, may therefore solve the most pressing problems of the SM. The only trouble is that we will never be able to test it experimentally, since the masses of N2,3 are beyond the reach of any current or future experiment.
Experimental opportunities
It is very difficult to detect HNLs experimentally. Indeed, if the masses of these particles are within the reach of current and planned accelerators, they must interact orders of magnitude more weakly than the ordinary weak interactions. As for the dark-matter sterile neutrino, the most promising route is indirect detection with X-ray space telescopes. The new X-ray spectrometer XRISM, which is planned to be launched this year, has great potential to unambiguously detect a signal from dark-matter decay. Like many astrophysical observatories, however, it will not be able to determine the particle origin of this signal. Thus, complementary laboratory searches are needed. One experimental proposal that claims a sufficient sensitivity to enter into the cosmologically relevant region is HUNTER, based on radioactive atom trapping and high-resolution decay-product spectrometry. Sterile neutrinos with masses of around a keV can also show up as a kink in the β-decay spectrum of radioactive nuclei, as discussed by the ambitious PTOLEMY proposal. The current generation of experiments that study β-decay spectra – KATRIN and Troitsk nu-mass – also perform searches for keV HNLs, but they are sensitive to significantly larger mixing angles than required for a dark-matter particle. Extending the KATRIN experiment with a multi-pixel silicon drift detector, TRISTAN, will significantly improve the sensitivity here.
The most promising perspectives to find N2,3 responsible for neutrino masses and baryogenesis are experiments at the intensity frontier. For HNL masses below 5 GeV (the beauty threshold) the best strategy is to direct proton beams at a target to create K, D or B mesons that decay producing HNLs, and then to search for HNL decays through “nothing → leptons and hadrons” processes in a near detector. This strategy was used in the previous PS191 experiment at CERN’s Proton Synchrotron (PS), NOMAD, BEBC and CHARM at the Super Proton Synchrotron (SPS) and NuTeV at Fermilab. There are several proposals for future experiments along these lines. The proposed SHiP experiment at the SPS Beam Dump Facility has the best potential as it can potentially cover almost all parameter space down to the lowest bound on coupling constants coming from neutrino masses. The SHiP collaboration has already performed detailed studies and beam tests, and the experiment is under consideration by the SPS and PS experiments committee. A smaller-scale proposal, SHADOWS, covers part of the interesting parameter space.

The search for HNLs can be carried out at the near detectors of DUNE at Fermilab and T2K/T2HK in Japan, which are due to come online later this decade. The LHC experiments ATLAS, CMS, LHCb, FASER and SND, as well as the proposed CODEX-b facility, can also be used, albeit with fewer chances to enter deeply into the cosmologically interesting part of the HNL parameter space. The decays of HNLs can also be searched for at future huge detectors such as MATHUSLA. And, going to larger HNL masses, breakthroughs can be made at the proposed Future Circular Collider FCC-ee, studying the processes Z → νN with a displaced vertex (DV) corresponding to the subsequent decay of N to available channels (see “Electron coupling” figure).
Conclusions
Neutrino experiments and robust conclusions from observational cosmology call for extensions of the SM. But the situation is very different from that in the period preceding the discovery of the Higgs boson, where the consistency of the SM together with other experimental results allowed us to firmly conclude that either the Higgs boson had to be discovered at the LHC, or new physics beyond the SM must show up. Although we know for sure that the SM is incomplete, we do not have a firm prediction about where to search for new particles nor what their masses, spins, interaction types and strengths are.
Experimental guidance and historical experience suggest that the SM should be extended in the fermion sector, and the completion of the SM with three Majorana fermions solves the main observational problems of the SM at once. If this extension of the SM is correct, the only new particles to be discovered in the future are three Majorana fermions. They have remained undetected so far because of their extremely weak interactions with the rest of the world.
Further reading
S Alekhin et al. 2016 Rept. Prog. Phys. 79 124201.
A Boyarsky et al. 2009 Ann. Rev. Nucl. Part. Sci. 59 191.
A Boyarsky et al. 2019 Prog. Part. Nucl. Phys. 104 1.