There is renewed interest in an old surprise.
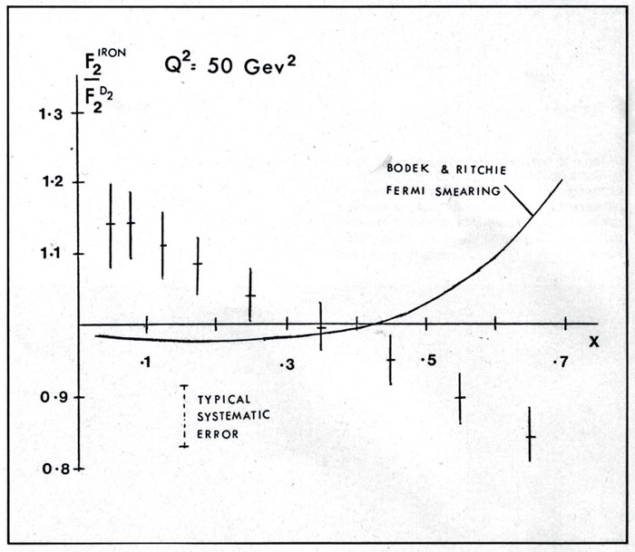
Contrary to the stereotype, advances in science are not typically about shouting “Eureka!”. Instead, they are about results that make a researcher say, “That’s strange”. This is what happened 30 years ago when the European Muon collaboration (EMC) at CERN looked at the ratio of their data on per-nucleon deep-inelastic muon scattering off iron and compared it with that of the much smaller nucleus of deuterium.
The data were plotted as a function of Bjorken-x, which in deep-inelastic scattering is interpreted as the fraction of the nucleon’s momentum carried by the struck quark. The binding energies of nucleons in the nucleus are several orders of magnitude smaller than the momentum transfers of deep-inelastic scattering, so, naively, such a ratio should be unity except for small corrections for the Fermi motion of nucleons in the nucleus. What the EMC experiment discovered was an unexpected downwards slope to the ratio (figure 1) – as revealed in CERN Courier in November 1982 and then published in a refereed journal the following March (Aubert et al. 1983).
This surprising result was confirmed by many groups
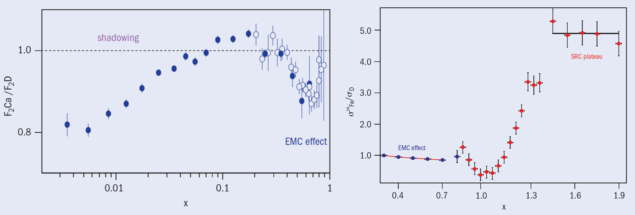
This surprising result was confirmed by many groups, culminating with the high-precision electron- and muon-scattering data from SLAC (Gomez et al. 1994), Fermilab (Adams et al. 1995) and the New Muon collaboration (NMC) at CERN (Amaudruz et al. 1995 and Arneodo et al. 1996). Figure 2 shows representative data. The conclusions from the combined experimental evidence were that: the effect had a universal shape; was independent of the squared four-momentum transfer, Q2; increased with nuclear mass number A; and scaled with the average nuclear density.
A simple picture
The primary theoretical interpretation of the EMC effect – the region x > 0.3 – was simple: quarks in nuclei move throughout a larger confinement volume and, as the uncertainty principle implies, they carry less momentum than quarks in free nucleons. The reduction of the ratio at lower x, named the shadowing region, was attributed either to the hadronic structure of the photon or, equivalently, to the overlap in the longitudinal direction of small-x partons from different nuclei. These notions gave rise to a host of models: bound nucleons are larger than free ones; quarks in nuclei move in quark bags with 6, 9 and even up to 3A quarks, where A is the total number of nucleons. More conventional explanations, such as the influence of nuclear binding, enhancement of pion-cloud effects and a nuclear pionic field, were successful in reproducing some of the nuclear deep-inelastic scattering data.
It was even possible to combine different models to produce new ones; this led to a plethora of models that reproduced the data (Geesaman et al. 1995), causing one of the authors of this article to write that “EMC means Everyone’s Model is Cool”. It is interesting to note that none of the earliest models were that concerned with the role of two-nucleon correlations, except in relation to six-quark bags.
The initial excitement was tempered as deep-inelastic scattering became better understood and the data became more precise. Some of the more extreme models were ruled out by their failure to match well known nuclear phenomenology. Moreover, inconsistency with the baryon-momentum sum rules led to the downfall of many other models. Because some of them predicted an enhanced nuclear sea, the nuclear Drell-Yan process was suggested as a way to disentangle the various possible models. In this process, a quark from a proton projectile annihilates with a nuclear antiquark to form a virtual photon, which in turn becomes a leptonic pair (Bickerstaff et al. 1984). The experiment was done and none of the existing models provided an accurate description of both sets of data – a challenge that remains to this day (Alde et al. 1984).
New data
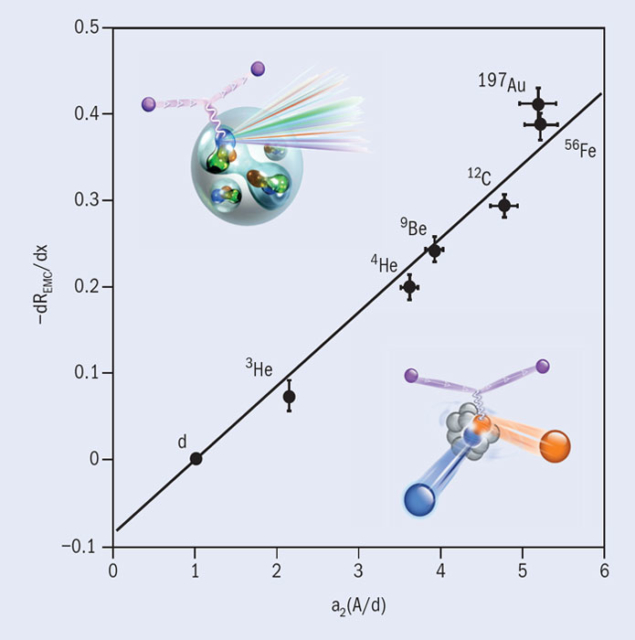
A significant shift in the experimental understanding of the EMC effect occurred when new data on 9Be became available (Seely et al. 2009). These data changed the experimental conclusion that the EMC effect follows the average nuclear density and instead suggested that the effect follows local nuclear density. In other words, even in deep-inelastic kinematics, 9Be seemed to act like two alpha particles with a single nearly free neutron, rather than like a collection of nucleons whose properties were all modified.
This led experimentalists to ask if the x > 1 scaling plateaux that have been attributed to short-range nucleon–nucleon correlations – a phenomenon that is also associated with high local densities – could be related to the EMC effect. Figure 3 shows the kinematic range of the EMC effect together with the x > 1 short-range correlation (SRC) region. While the dip at x = 1 has been shown to vary rapidly with Q2, the EMC effect and the magnitude of the x > 1 plateaux are basically constant within the Q2 range of the experimental data. Plotting the slope of the EMC effect, 0.3 < x < 0.7, against the magnitude of scaling x > 1 plateaux for all of the available data, as shown in figure 4, revealed a striking correlation (Weinstein et al. 2011). This phenomenological relationship has led to renewed interest in understanding how strongly correlated nucleons in the nucleus may be affecting the deep-inelastic results.
In February 2013, on nearly the 30th anniversary of the EMC publication, experimentalists and theorists came together at a special workshop at the University of Washington Institute of Nuclear Theory to review understanding of the EMC effect, discuss recent advances and plan new experimental and theoretical efforts. In particular, an entire series of EMC and SRC experiments are planned for the new 12 GeV electron beam at Jefferson Lab and analysis is underway of new Drell-Yan experimental data from Fermilab.
A new life
Although the EMC effect is now 30 years old, the recent experimental results have given new life to this old puzzle; no longer is Every Model Cool. Understanding the EMC effect implies understanding how partons behave in the nuclear medium. It thus has far-reaching consequences for not only the extraction of neutron information from nuclear targets but also for understanding effects such as the NuTeV anomaly or the excesses in the neutrino cross-sections observed by the MiniBooNe experiment.





