What ultimately controls the way particles interact? Different particles appear to interact at high energies in similar ways through a mechanism known as pomeron exchange. Sandy Donnachie explains what we know about the pomeron.
Particle physics experiments ultimately depend on the way pairs of particles scatter off each other. A simple example of scattering is a game of billiards, in which the cue ball scatters off the other balls in carefully chosen directions. In physics language, billiards is an “elastic scattering” the balls simply bounce off each other. While in billiards the balls do not shatter, in elementary particle scattering the objective is usually to create havoc, the balls knocking bits off each other or even disintegrating totally, creating new balls in a complicated game of snooker that is played under the rules of relativity and quantum mechanics.

The interaction of ordinary billiard balls can be understood by their elasticity. After an initial compression as they collide, two balls subsequently spring back into shape and recoil away. For the more complex process of particle interactions, physicists understand the interaction via invisible particles transferring momentum from one visible particle to another as they pass each other. Such an “exchange process” is illustrated in figure 1, which shows the electromagnetic interaction between two electrons mediated by the exchange of an invisible light quantum or “photon”.
For the high-energy scattering of particles that feel the strong force, such as protons, the same physical concept applies, but now the exchange is made by whole families of related particles. One such is the rho family, named after its lightest member, the spin-1 rho meson, which comprises the rho and its cousin spin-3, spin-5, …. recurrences at higher mass.
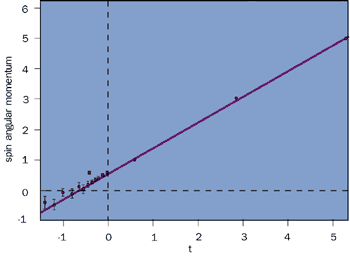
Regge theory (after the Italian physicist Tullio Regge) gives the collective effect of the exchange of all of the members of such a family in terms of a Regge trajectory a(t), which is described mathematically as a function of the invariant momentum transfer, t. The rho trajectory is shown in figure 2 for the “time-like” region of positive t corresponding to the real physical particles of spin-1, spin-3, spin-5, etc, and in the “space-like” region of negative t relevant for the exchange in a scattering process. The trajectory is well described by a straight line: a(t) = a0 + a‘t = 0.55 + 0.86t. This is an experimental result: it cannot be predicted by Regge theory. It turns out that the trajectories of all of the dominant meson-exchange families lie close to this line they are almost degenerate.
Regge theory
Regge theory tells us that the energy dependence of the sum of everything that happens the “total cross-section” is dependent on the value of the trajectory at t = 0. Specifically, it is given by the square of the collision energy, s, raised to the power a0-1. As all of the meson trajectories are nearly degenerate and have a0 = 0.55, the energy dependence is s-0.45, roughly as the inverse of the square root of s, so the prediction of Regge theory for meson exchange is that the cross-section should decrease with increasing energy and do so at a well defined rate.
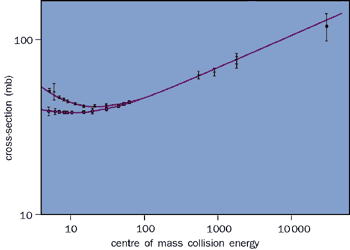
While such behaviour is indeed seen at collision energies below about 15 GeV, at higher energies the total cross-section at first flattens out and then begins to rise slowly, an effect first hinted at in cosmic-ray data, demonstrated unambiguously for the first time at the CERN ISR Intersecting Storage Rings and the rising trend confirmed at the CERN’s protonantiproton collider and at Fermilab’s Tevatron. The cross-section for protonproton and protonantiproton scattering is shown in figure 3. The simplest assumption to make is that this rising cross-section is due to the exchange of another Regge trajectory and so also gives a simple power of s. To produce a rising cross-section it must be such that a0 = 1 + e with e positive. This is the phenomenological or “soft” pomeron, named after the Russian physicist Igor Pomeranchuk.
The parameter e is universal, independent of the particles being scattered. Fitting the total cross-sections for protonproton, protonantiproton, positive and negative pionproton, positive and negative kaonproton and photonproton scattering over the centre of-mass energy range 10 GeV to 1.8 TeV gives e = 0.095. Extrapolation to cosmic-ray energies of 30 TeV shows no deviation from the fit. However, the data errors are much greater than those at current accelerator energies and we will need to await the arrival of the LHC to provide the precise data necessary to test the theory fully at these very high energies.
Physical particles have quarks as their constituents: three quarks for the proton and antiproton, plus a quark and an antiquark for the mesons. One view of high-energy particle scattering is that the pomeron interacts with these valence quarks. In the fits to the total cross-sections the ratios of the strengths of pomeron exchange in pionproton and protonproton or protonantiproton scattering is almost exactly 2/3. This can be taken as evidence that the pomeron does indeed couple to single valence quarks in a hadron the “additive quark rule”.
An alternative viewpoint is that the pomeron interacts both with the valence quarks and with the gluons that bind the quarks together to form the physical particles, and the cross-section ratios simply reflect the different sizes of these particles. This issue is still unresolved.





