Borexino and KamLAND make the first measurements of Earth’s neutrinos.

Image credit: Borexino collaboration.
The journal Science celebrated its 125th anniversary in 2005 and in a special issue listed what it considered to be the top 25 questions facing scientists during the next quarter of a century (Kerr 2005). These questions included: how does the Earth̓s interior work?
The main geophysical and geochemical processes that have driven the evolution of the Earth are strictly bound by the planet̓s energy budget. The current flux of energy entering the Earth’s atmosphere is well known: the main contribution comes from solar radiation (1.4 × 103 W m–2), while the energy deposited by cosmic rays is significantly smaller (10–8 W m–2). The uncertainties on terrestrial thermal power are larger – although the most quoted models estimate a global heat loss in the range of 40–47 TW, a global power of 30 TW is not excluded. The measurements of the temperature gradient taken from some 4 × 104 drill holes distributed around the world provide a constraint on the Earth’s heat production. Nevertheless, these direct investigations fail near the oceanic ridge, where the mantle content emerges: here hydrothermal circulation is a highly efficient heat-transport mechanism.
The generation of the Earth’s magnetic field, its mantle circulation, plate tectonics and secular (i.e. long lasting) cooling are processes that depend on terrestrial heat production and distribution, and on the separate contributions to Earth’s energy supply (radiogenic, gravitational, chemical etc.). An unambiguous and observationally based determination of radiogenic heat production is therefore necessary for understanding the Earth’s energetics. Such an observation requires determining the quantity of long-lived radioactive elements in the Earth. However, the direct geochemical investigations only go as far as the upper portion of the mantle, so all of the geochemical estimates of the global abundances of heat-generating elements depend on the assumption that the composition of meteorites reflects that of the Earth.

The uranium and thorium decay chains and 40K contribute about 99% of the total radiogenic heat production of the Earth; however, both the total amount and the distribution of these elements inside the Earth remain open to question. Thorium and uranium are refractory lithophile elements, while potassium is volatile. The processes of accretion and differentiation of the early Earth, as well as the subsequent processes of recycling and dehydrating subducting slabs, further enhance the concentrations of these radioactive elements in the crust. According to Roberta Rudnick and Shan Gao, the radiogenic heat production of the crust is 7.3 ± 1.2 (1σ) TW (Rudnick and Gao 2003).
The expected amount and distribution of uranium, thorium and potassium in the mantle are model dependent. The Bulk Silicate Earth (BSE) is a canonical model that provides a description of geological evidence that is coherent within the constraints placed by the combined studies of mantle samples and the most primitive of all of the meteorites – the CI group of carbonaceous chondrites – which have a chemical composition similar to that of the solar photosphere, neglecting gaseous elements. The model predicts a radiogenic heat production in the mantle of about 13 TW. However, it needs to be tested because, on the grounds of available geochemical and/or geophysical data, it is not possible to exclude the theory that the radioactivity in the Earth today is enough to account for the highest estimate of the total terrestrial heat. Some models are based on a comparison of the planet with other chondrites, such as enstatite chondrites, and alternative hypotheses do not exclude the presence of radioactive elements in the Earth’s core. In addition, other models suggest the existence of a geo-reactor of 3–6 TW induced by important amounts of uranium present around the core. The debate remains open.
Neutrinos from the Earth
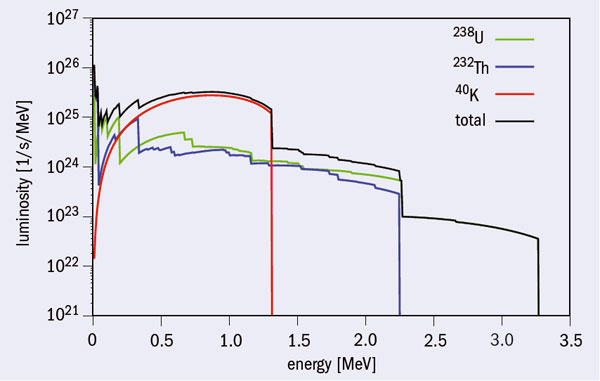
Geo-neutrinos are the (anti)neutrinos produced by the natural radioactivity inside the Earth. In particular, the decay chains of 238U and 232Th include six and four β− decays, respectively, and the nucleus of 40K decays by electron capture and β− decay with branching ratios of 11% and 89%, respectively. The decays produce heat and electron antineutrinos, with fixed ratios of heat to neutrinos (table 1). A measurement of the antineutrino flux, and possibly of the spectrum, would provide direct information on the amount and composition of radioactive material inside the Earth and so would determine the radiogenic contribution to the heat flow.

Image credit: Berkeley KamLAND group.
The Earth emits mainly in electron-antineutrinos, while the Sun shines in electron-neutrinos. The order of magnitude of the antineutrino flux on the surface, following the model hypotheses, could be 106 cm–2 s–1 from uranium and thorium in the Earth and 107 cm–2 s–1 from potassium, as compared with a neutrino flux of 6 × 1010 cm–2 s–1 from the Sun. Given the two types of crust (continental and oceanic) and their different composition and thickness, the expected flux of geo-neutrinos differs from place to place on the Earth’s surface. Moreover, considering that this variation can be as much as an order of magnitude, a detector’s sensitivity to geo-neutrinos coming from the mantle and the crust will depend on its location.
The process for the detection of low-energy antineutrinos used by the detectors currently running (KamLAND at Kamioka, Japan, and Borexino at Gran Sasso, Italy) and under construction (SNO+ at SNOlab, Canada), is inverse beta decay with a threshold of 1.806 MeV. Hence, only a fraction of the geo-neutrinos from 238U and 232Th are above threshold (figure 1), and the detection of antineutrinos from 40K remains a difficult challenge even for the next generation detectors. These experiments use liquid scintillator as the detecting material: one kilotonne of it contains some 1032 protons. As a consequence the event rate is conveniently expressed in terms of terrestrial neutrino units (TNU), defined as one event per 1032 target protons a year.
In the underground experiments devoted to the measurement of geo-neutrinos, liquid scintillator – essentially hydrocarbons – provides the hydrogen nuclei that act as the target for the antineutrinos. In these detectors a geo-neutrino event is tagged by a prompt signal and a delayed signal, following the inverse beta decay: ν–e + p → e+ + n – 1.806 MeV.
The positron ionization and annihilation provide the prompt signal. The energy of the incoming neutrino is related to the measured energy by the relationship: Eν = Emeasured + 0.782 MeV. The prompt signal is in the energy range (1.02, 2.50) MeV for uranium and (1.02, 1.47) MeV for thorium. The neutron slows down and after thermalization is captured by a proton, making a deuteron and a gamma ray of 2.22 MeV. The gamma ray generates the delayed signal. In large volumes of liquid scintillator the delayed signal is fully contained with an efficiency of around 98%.
The prompt–delayed sequence of the inverse beta decay provides a strong tag for electron antineutrinos, well known since the pioneering experiment of Clyde Cowan and Fred Reines in 1956. There is a correlation in space and time between the prompt and delayed signals. The correlated time depends on the properties of the scintillator and is in the order of 200–250 μs. The correlated distance between the two signals is related to the spatial resolution of the detector (around 10 cm at 1 MeV) and is driven by Compton interactions – with a probability of about 100% it can be less than 1 m.
Any electron-antineutrinos besides the ones produced within the Earth, and any event that can mimic a prompt–delayed signal with a neutron in the final state, can be a source of background. In particular, consider electron-antineutrinos produced by nuclear power reactors. Their energy spectrum partially overlaps the one for geo-neutrinos, but shifted towards higher energies up to about 10 MeV. Some 400 power reactors exist, mainly in North America, Europe, West Russia and Japan. Therefore, depending on the location of the underground laboratories, this background can produce a significant interference with the detection of geo-neutrinos.
Among other background sources there are (α,n) reactions resulting from contaminants in the scintillator, such as 210Po, and cosmogenic radioactive isotopes such as 9Li and 8He, which are produced by muons crossing the laboratory overburden. 9Li and 8He decay through beta-delayed neutron emission with T1/2 = 178.3 ms and 119 ms, respectively. Using dead-time, a cut of 2 s after each detected muon crossing the liquid scintillator, can reject this background with an efficiency of 99.9%. A high level of radiopurity and a fiducial mass cut will reduce uncorrelated random coincidences, which can arise from impurities such as 210Bi, 214Bi and 208Tl.
Detecting geo-neutrinos
The first attempt to detect geo-neutrinos was made by the KamLAND experiment in 2005, where a signal was detected at the 2σ level (Araki et al. 2005). Three years later the same experiment reported a second measurement at 2.7σ (Abe et al. 2008). In 2010 Borexino reported evidence of geo-neutrinos at 4.2σ (Bellini et al. 2010). This was followed by a measurement in KamLAND with the same significance (Inoue 2010 and Shimizu 2010). The KamLAND and the Borexino experiments both make use of a large mass of organic liquid scintillator shielded by a large-volume water Cherenkov detector and viewed by a large number of photomultipliers (around 2000). In KamLAND in particular, a fiducial mass of around 700 tonnes can be selected, whereas in Borexino the maximum target mass can be as much as 280 tonnes. The statistics of the KamLAND measurement is higher than in Borexino owing to the larger volume and longer exposure; on the other hand the signal-to-noise ratio in the geo-neutrino spectrum window is about 2 for Borexino and about 0.15 for KamLAND.
The interesting quantity is the flux of geo-neutrinos in a given location on the Earth’s surface. This depends on the spatial distribution of the heat-generating elements within the Earth. Geo-neutrinos can travel as much as some 12,000 km to the detector. Therefore, the measured flux of geo-neutrinos must include the effect of neutrino oscillations. It turns out that for geo-neutrinos, the global effect of oscillations is reduced to a constant suppression of the flux through an average survival probability, <Pee >, of around 0.57.
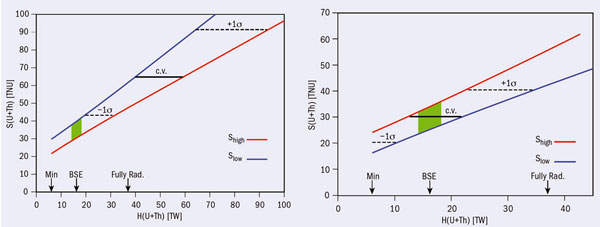
The number of observed geo-neutrino events in KamLAND is 106 + 29 – 28 (+89–78) at 1σ (3σ) with 2135 live-days and a target mass of about 670 tonnes. Borexino has observed 9.9 + 4.1 – 3.4(+ 14.6 – 8.2) geo-neutrino events in 482 days and 225 tonnes at 1σ (3σ). The rate in TNU for the Borexino and KamLAND observations corresponds to 64.8 + 26.6 – 21.6 and 38.3+10.3–9.9, respectively. In fits to the detected data in both experiments, the shapes of the geo-neutrino spectra are the same as in figure 1, assuming the chondritic Th/U mass ratio of 3.9. The combined KamLAND and Borexino observation has a significance of 5σ (Fogli et al. 2010). Figure 2 shows the allowed range for geo-neutrino rates in Borexino and KamLAND as a function of the Earth’s radiogenic heat. The minimum radiogenic heat of Earth corresponds only to the crust contribution.
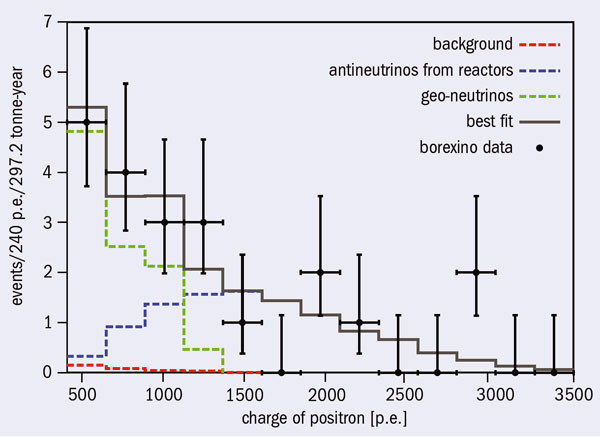
The signal-to-noise ratio for reactor antineutrino background in the geo-neutrino energy range is a fundamental parameter for geo-neutrino observations. In Borexino in particular this ratio – neglecting other backgrounds – is around 1.3 because there are no nearby nuclear reactors. Indeed, at Gran Sasso the weighted distance to reactors <Lreac> is about 1000 km. By contrast, at Kamioka <Lreac> is around 200 km with a signal-to-noise ratio of about 0.2. Therefore, at present the significance of the Borexino measurement is limited only by the statistics (figure 3). This indicates that a spectroscopic measurement of the geo-neutrino signal is feasible, taking into account the overall low background rate.
In a few years a third detector, SNO+, with a weighted reactor distance <Lreac> of around 480 km should be operational. A combined analysis of the Borexino, KamLAND and SNO+ experiments could constrain the radiogenic heat of the mantle. In the long term, LENA – a super-massive detector of about 50 kilotonnes – could observe as many as 1000 geo-neutrinos a year. LENA would be located at the Centre for Underground Physics at Pyhäsalmi in Finland with <Lreac> of around 1000 km.
• The authors acknowledge some interesting discussions with W F McDonough, R L Rudnick and G Fiorentini.





