Charming clues for existence

In November 1974, the research groups of Samuel Ting at Brookhaven National Laboratory and Burton Richter at SLAC independently discovered a resonance at 3.1 GeV that was less than 1 MeV wide. Posterity soon named it J/ψ, juxtaposing the names chosen by each group in a unique compromise. Its discovery would complete the second generation of fermions with the charm quark, giving experimental impetus to the new theories of electroweak unification (1967) and quantum chromodynamics (1973). But with the theories fresh and experimenters experiencing an annus mirabilisfollowing the indirect discovery of the Z boson in neutral currents the year before, the nature of the J/ψ was not immediately clear.

“Why the excitement over the new discoveries?” asked the Courier in December 1974 (see “The new particles“). “A brief answer is that the particles have been found in a mass region where they were completely un­expected, with stability properties which, at this stage of the game, are completely inexplicable.”

The J/ψ is now known to be made up of a charm quark and a charm antiquark. Unable to decay via the strong interaction, its width is just 92.6 keV, corresponding to an unexpectedly long lifetime of 7.1 × 10^–21 s. Charm quarks do not form ordinary matter like protons and neutrons, but J/ψ resonances and D mesons, which contain a charm quark and a less-massive up, down or strange antiquark.

Fifty years on from the November Revolution, charm physics is experiencing a renaissance. The LHCb, BESIII and Belle II experiments are producing a huge number of interesting and precise measurements in the charm system, with two crucial groundbreaking results on D⁰ mesons by LHCb holding particular significance: the observation that they violate CP symmetry when they decay; and the observation that they oscillate into their antiparticles. The rate of CP violation is particularly interesting – about 10 times larger than the most sophisticated Standard Model (SM) predictions, preliminary and uncertain though they are. Are these predictions naive, or is this the first glimpse of why there is more matter than antimatter in the universe?

Suppressed

Despite the initial confusion, the charm quark had already been indirectly discovered in 1970 by Sheldon Glashow, John Iliopoulos and Luciano Maiani (GIM), who introduced it to explain why K⁰ → μ⁺μ^– decays are suppressed. Their paper gained widespread recognition during the November Revolution, and the GIM mechanism they discovered impacts cutting-edge calculations in charm physics to this day.

Previously, only the three light quarks (up, down and strange) were known. Alongside electrons and electron neutrinos, up and down quarks make up the first generation of fermions. The detection of muons in cosmic rays in 1936 was the first evidence for a second generation, triggering Isidor Rabi’s famous exclamation “Who ordered that?” Strange particles were found in 1947, providing evidence for a second generation of quarks, though it took until 1964 for Murray Gell-Mann and George Zweig to discover this ordering principle of the subatomic world.

In a model of three quarks, the decay of a K⁰ meson (a down–antistrange system) into two muons can only proceed by briefly transforming the meson into a W⁺W^– pair – an infamous flavour-changing neutral current – linked in a loop by a virtual up quark and virtual muon neutrino. While the amplitude for this process is problematically large given observed rates, the GIM mechanism cancels it almost exactly by introducing destructive quantum interference with a process that replaces the up quark with a new charm quark. The remaining finite value of the amplitude stems from the difference in the masses of the virtual quarks compared to the W boson, m_u²/M_W² and m_c²/M_W². Since both mass ratios are close to zero, K⁰ → μ⁺μ^– is highly suppressed.

The interference is destructive because the Cabibbo matrix describing the coupling strength of the charged weak interaction is a rotation of the two generations of quarks. All four couplings in the matrix – up–down (cos θ_C), charm-strange (cos θ_C), charm-down (sin θ_C) and up-strange (–sin θ_C) – arise in the decay of a K⁰ meson, with the minus sign causing the cancellation.

Maybe the charm quark will in the end provide the ultimate clue to explain our existence

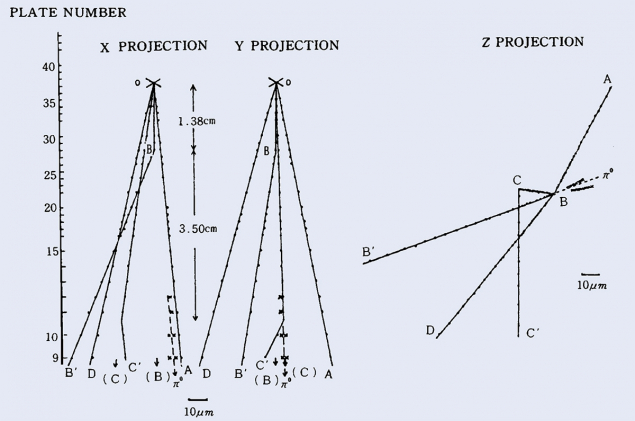
The direct experimental detection of the first particle containing charm is typically attributed to Ting and Richter in 1974, however, there was already some direct evidence for charmed mesons in Japan in 1971, though unfortunately in only one cosmic-ray event, and with no estimation of background (see “Cosmic charm” figure). Unnoticed by Western scientists, the measurements indicated a charm-quark mass of the order of 1.5 GeV, which is close to current estimates. In 1973, the quark-mixing formalism was extended by Makoto Kobayashi and Toshihide Maskawa to three generations of quarks, incorporating CP violation in the SM by allowing the couplings to be complex numbers with an imaginary part. The amount of CP violation contained in the resulting Cabibbo–Kobayashi–Maskawa (CKM) matrix does not appear to be sufficient to explain the observed matter–antimatter asymmetry in the universe.

The third generation of quarks began to be experimentally established in 1977 with the discovery of ϒ resonances (bottom–antibottom systems). In 1986, GIM cancellations in the matter–antimatter oscillations of neutral B mesons (B⁰–B⁰ mixing) indicated a large value of the top-quark mass, with m_t²/M_W² not negligible, in contrast to m_u²/M_W² and m_c²/M_W². The top quark was directly discovered at the Tevatron in 1995. With the discovery of the Higgs boson in 2012 at the LHC, the full particle spectrum of the SM has now been experimentally confirmed.

Charm renaissance

More recently, two crucial effects in the charm system have been experimentally confirmed. Both measurements present intriguing discrepancies by comparison with naive theoretical expectations.

First, in 2019, the LHCb collaboration at CERN observed the first definitive evidence for CP violation in charm. A difference in the behaviour of matter and antimatter particles, CP violation can be expressed directly in charm decays, indirectly in the matter–antimatter oscillations of charmed particles, or in a quantum admixture of both effects. To isolate direct CP violation, LHCb proved that the difference in matter–antimatter asymmetries seen in D⁰ → K⁺K^– and D⁰ → π⁺π^– decays (ΔA_CP) is nonzero. Though the observed CP violation is tiny, it is nevertheless approximately a factor 10 larger than the best available SM predictions. Currently the big question is whether these naive SM expectations can be enhanced by a factor of 10 due to non-perturbative effects, or whether the measurement of ΔA_CP is a first glimpse of physics beyond the SM, perhaps also answering the question of why there is more matter than antimatter in the universe.

Two years later, LHCb definitively demonstrated the transformation of neutral D⁰ mesons into their antiparticles (D⁰–D⁰mixing). These transitions only involve virtual down-type quarks (down, strange and bottom), causing extreme GIM cancellations as m_d²/M_W², m_s²/M_W²  and m_b²/M_W² are all negligible (see “Matter–antimatter mixing” figure). Theory calculations are preliminary here too, but naive SM predictions of the mass splitting between the mass eigenstates of the neutral D-meson system are at present several orders of magnitude below the experimental value.

The charm system has often proved to be more experimentally challenging than the bottom system, with matter–antimatter oscillations and direct and indirect CP violation all discovered first for the bottom quark, and indirect CP violation still awaiting confirmation in charm. The theoretical description of the charm system also presents several interesting features by comparison to the bottom system. They may be regarded as challenges, peculiarities, or even opportunities.

A challenge is the use of perturbation theory. The strong coupling at the scale of the charm-quark mass is quite large – α_s(m_c) ≈ 0.35 – and perturbative expansions in the strong coupling only converge as (1, 0.35, 0.12, …). The charm quark is also not particularly heavy, and perturbative expansions in Λ/m_c only converge as roughly (1, 0.33, 0.11, …), assuming Λ is an energy scale of the order of the hadronic scale of the strong interaction. If the coefficients being multiplied are of similar sizes, then these series may converge.

Numerical cancellations are a peculiarity, and often classified as strong or even crazy in cases such as D⁰–D⁰ mixing, where contributions cancel to one part in 10⁵.

The fact that CKM couplings involving the charm quark (V_cd, V_cs and V_cb) have almost vanishing imaginary parts is an opportunity. With CP-violating effects in charm systems expected to be tiny, any measurement of sizable CP violating effects would indicate the presence of physics beyond the SM (BSM).

A final peculiarity is that loop-induced charm decays and D-mixing both proceed exclusively via virtual down-type quarks, presenting opportunities to extend sensitivity to BSM physics via joint analyses with complementary bottom and strange decays.

At first sight, these effects complicate the theoretical treatment of the charm system. Many approaches are therefore based on approximations such as SU(3)_F flavour symmetry or U-spin symmetry (see “Using U-spin to squeeze CP violation”). On the other hand, these properties can also be a virtue, making some observables very sensitive to higher orders in our expansions and providing an ideal testing ground for QCD tools.

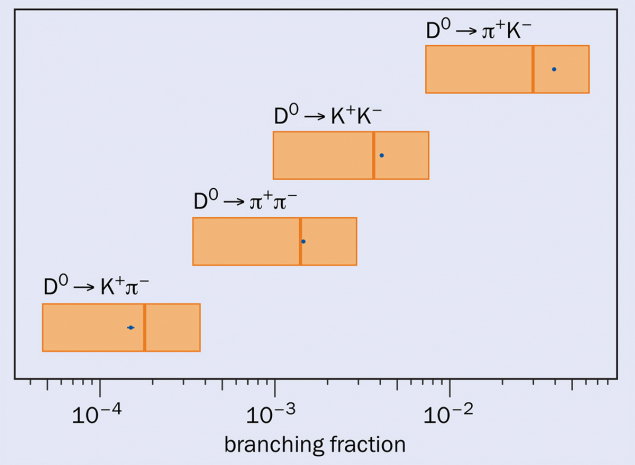
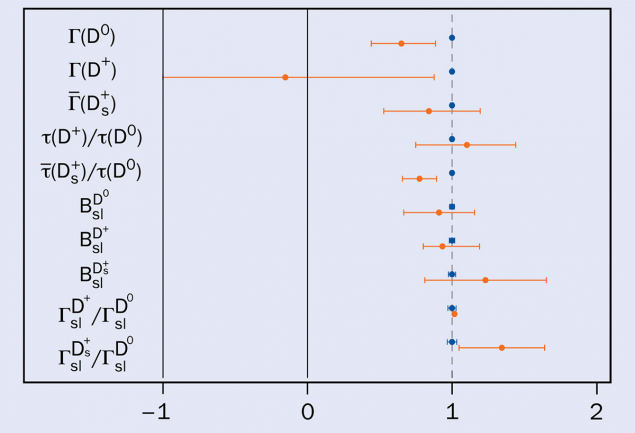
Thanks to many theoretical improvements, we are now in a position to start answering the question of whether perturbative expansions in the strong coupling and the inverse of the quark mass are applicable in the charm system. Recently, progress has been made with observables that are free from severe cancellations: a double expansion in Λ/m_cand α_s (the heavy-quark expansion) seems to be able to reproduce the D⁰ lifetime (see “Charmed life” figure); and theoretical calculations of branching fractions for non-leptonic two-body D⁰ decays seem to be in good agreement with experimental values (see “Two body” figure).

All these theory predictions still suffer from large uncertainties, but they can be systematically improved. Demonstrating the validity of these theory tools with higher precision could imply that the measured value of CP violation in the charm system (ΔA_CP) has a BSM origin.

The future

Charm physics therefore has a bright future. Many of the current theory approaches can be systematically improved with currently available technologies by adding higher-order perturbative corrections. A full lattice-QCD description of D-mixing and non-leptonic D-meson decays requires new ideas, but first steps have already been taken. These theory developments should give us deeper insights into the question of whether ΔA_CP and D⁰–D⁰ mixing can be described within the SM.

More precise experimental data can also help in answering these questions. The BESIII experiment at IHEP in China and the Belle II experiment at KEK in Japan can investigate inclusive semileptonic charm decays and measure parameters that are needed for the heavy-quark expansion. LHCb and Belle II can investigate CP-violating effects in D⁰–D⁰ mixing and in channels other than D⁰ → K⁺K^– and π⁺π^–. The super tau–charm factory proposed by China could contribute further precise data and a future e⁺e^– collider running as an ultimate Z factory could provide an independent experimental cross-check for ΔA_CP.

Another exciting field is that of rare charm decays such as D⁺ → π⁺μ⁺μ^– and D⁺ → π⁺ νν, which proceed via loop diagrams similar to those in K⁰ → μ⁺μ^– decays and D⁰–D⁰ oscillations. Here, null tests can be constructed using observables that vanish precisely in the SM, allowing future experimental data to unambiguously probe BSM effects.

Maybe the charm quark will in the end provide the ultimate clue to explain our existence. Wouldn’t that be charming?