Who ordered all of that?

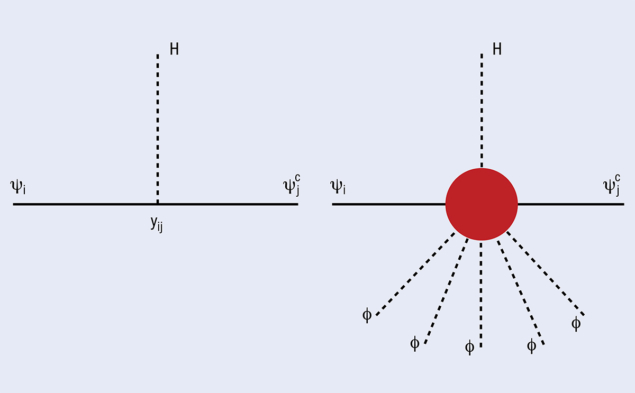
The origin of the three families of quarks and leptons and their extreme range of masses is a central mystery of particle physics. According to the Standard Model (SM), quarks and leptons come in complete families that interact identically with the gauge forces, leading to a remarkably successful quantitative theory describing practically all data at the quantum level. The various quark and lepton masses are described by having different interaction strengths with the Higgs doublet (figure 1, left), also leading to quark mixing and charge-parity (CP) violating transitions involving strange, bottom and charm quarks. However, the SM provides no understanding of the bizarre pattern of quark and lepton masses, quark mixing or CP violation.

In 1998 the SM suffered its strongest challenge to date with the decisive discovery of neutrino oscillations resolving the atmospheric neutrino anomaly and the long-standing problem of the low flux of electron neutrinos from the Sun. The observed neutrino oscillations require at least two non-zero but extremely small neutrino masses, around one ten millionth of the electron mass or so, and three sizeable mixing angles. However, since the minimal SM assumes massless neutrinos, the origin and nature of neutrino masses (i.e. whether they are Dirac or Majorana particles, the latter requiring the neutrino and antineutrino to be related by CP conjugation) and mixing is unclear, and many possible SM extensions have been proposed.

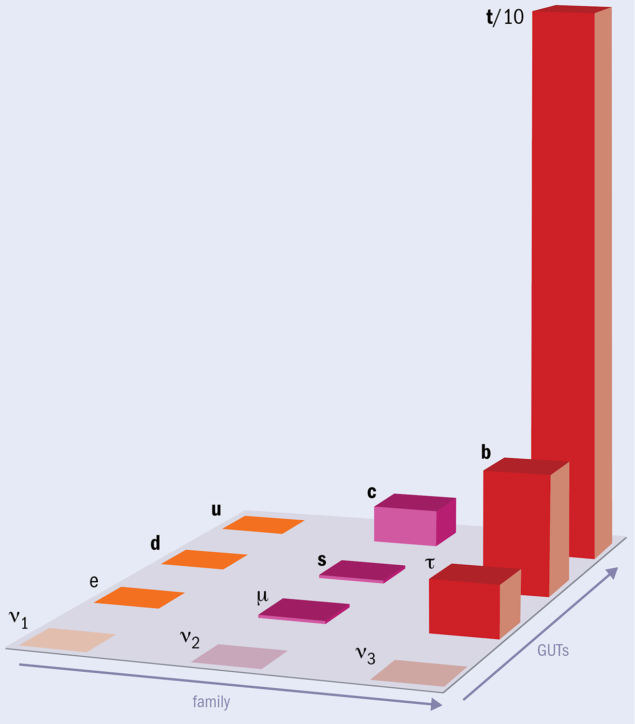
The discovery of neutrino mass and mixing makes the flavour puzzle hard to ignore, with the fermion mass hierarchy now spanning at least 12 orders of magnitude, from the neutrino to the top quark. However, it is not only the fermion mass hierarchy that is unsettling. There are now 28 free parameters in a Majorana-extended SM, including a whopping 22 associated with flavour, surely too many for a fundamental theory of nature. To restate Isidor Isaac Rabi’s famous question following the discovery of the muon in 1936: who ordered all of that?

A theory of flavour

There have been many attempts to formulate a theory beyond the SM that can address the flavour puzzles. Most attempt to enlarge the group structure of the SM describing the strong, weak and electromagnetic gauge forces: SU(3)_C × SU(2)_L × U(1)_Y (see “A taste of flavour in elementary particle physics” panel). The basic premise is that, unlike in the SM, the three families are distinguished by some new quantum numbers associated with a new family or flavour symmetry group, G_fl, which is tacked onto the SM gauge group, enlarging the structure to G_fl × SU(3)_C × SU(2)_L × U(1)_Y. The earliest ideas dating back to the 1970s include radiative fermion-mass generation, first proposed by Weinberg in 1972, who supposed that some Yukawa couplings might be forbidden at tree level by a flavour symmetry but generated effectively via loop diagrams. Alternatively, the Froggatt–Nielsen (FN) mechanism in 1979 assumed an additional U(1)_fl symmetry under which the quarks and leptons carry various charges.

To account for family replication and to address the question of large lepton mixing, theorists have explored a larger non-Abelian family symmetry, SU(3)_fl, where the three families are analogous to the three quark colours in quantum chromodynamics (QCD). Many other examples have been proposed based on subgroups of SU(3)_fl, including discrete symmetries (figure 2, right). More recently, theorists have considered extra-dimensional models in which the Higgs field is located at a 4D brane, while the fermions are free to roam over the extra dimension, overlapping with the Higgs field in such a way as to result in hierarchical Yukawa couplings. Still other ideas include partial compositeness in which fermions may get hierarchical masses from the mixing between an elementary sector and a composite one. The possibilities are seemingly endless. However, all such theories share one common question: what is the scale, M_fl, (or scales) of new physics associated with flavour?

Since experiments at CERN and elsewhere have thoroughly probed the electroweak scale, all we can say for sure is that, unless the new physics is extremely weakly coupled, M_fl can be anywhere from the Planck scale (10¹⁹GeV), where gravity becomes important, to the electroweak scale at the mass of the W boson (80 GeV). Thus the flavour scale is very unconstrained.

 

To illustrate the unknown magnitude of the flavour scale, consider for example the FN mechanism, where M_fl is associated with the breaking of the U(1)_fl symmetry. In the SM the top-quark mass of 173 GeV is given by a Yukawa coupling times the Higgs vacuum expectation value of 246 GeV divided by the square root of two. This implies a top-quark Yukawa coupling close to unity. The exact value is not important, what matters is that the top Yukawa coupling is of order unity. From this point of view, the top quark mass is not at all puzzling – it is the other fermion masses associated with much smaller Yukawa couplings that require explanation. According to FN, the fermions are assigned various U(1)_fl charges and small Yukawa couplings are forbidden due to a U(1)_fl symmetry. The symmetry is broken by the vacuum expectation value of a new “flavon” field <φ>, where φ is a neutral scalar under the SM but carries one unit of U(1)_fl charge. Small Yukawa couplings then originate from an operator (figure 1, right) suppressed by powers of the small ratio <φ>/M_fl (where M_fl acts as a cut-off scale of the contact interaction).

For example, suppose that the ratio <φ>/M_fl is identified with the Wolfenstein parameter λ = sinθ_C= 0.225 (where θ_C is the Cabibbo angle appearing in the CKM quark-mixing matrix). Then the fermion mass hierarchies can be explained by powers of this ratio, controlled by the assigned U(1)_fl charges: m_e/m_τ ∼ λ⁵, m_μ/m_τ ∼ λ², m_d/m_b ∼ λ⁴, m_s/m_b ∼ λ², m_u/m_t ∼ λ⁸ and m_c/m_t ∼  λ⁴. This shows how fermion masses spanning many orders of magnitude may be interpreted as arising from integer U(1)_fl charge assignments of less than 10. However, in this approach, M_fl may be anywhere from the Planck scale to the electroweak scale by adjusting <φ> such that the ratio λ = <φ>/M_fl is held fixed.

One possibility for M_fl, reviewed by Kaladi Babu at Oklahoma State University in 2009, is that it is not too far from the scale of grand unified theories (GUTs), of order 10¹⁶ GeV, which is the scale at which the gauge couplings associated with the SM gauge group unify into a single gauge group. The simplest unifying group, SU(5)_GUT, was proposed by Georgi and Glashow in 1974, following the work of Pati and Salam based on SU(4)_C × SU(2)_L × SU(2)_R. Both these gauge groups can result from SO(10)_GUT, which was discovered by Fritzsch and Minkowski (and independently by Georgi), while many other GUT groups and subgroups have also been studied (figure 2, left). However, GUT groups by themselves only unify quarks and leptons within a given family, and while they may provide an explanation for why m_b= 2.4 m_τ, as discussed by Babu, they do not account for the fermion mass hierarchies.

Broken symmetries

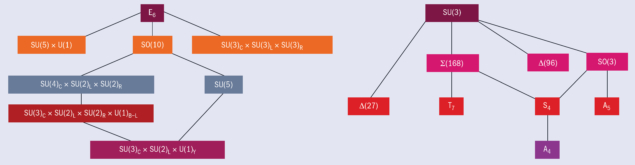
A way around this, first suggested by Ramond in 1979, is to combine GUTs with family symmetry based on the product group G_GUT × G_fl, with symmetries acting in the specific directions shown in the figure “Family affair”. In order not to spoil the unification of the gauge couplings, the flavour-symmetry breaking scale is often assumed to be close to the GUT breaking scale. This also enables the dynamics of whatever breaks the GUT symmetry, be it Higgs fields or some mechanism associated with compactification of extra dimensions, to be applied to the flavour breaking. Thus, in such theories, the GUT and flavour/family symmetry are both broken at or around M_fl ∼ M_GUT∼ 10¹⁶ GeV, as widely discussed by many authors. In this case, it would be impossible given known technology to directly experimentally access the underlying theory responsible for unification and flavour. Instead, we would need to rely on indirect probes such as proton decay (a generic prediction of GUTs and hence of these enlarged SM structures proposed to explain flavour) and/or charged-lepton flavour-violating processes such as μ → eγ (see CERN Courier May/June 2019 p45).

New ideas for addressing the flavour problem continue to be developed. For example, motivated by string theory, Ferruccio Feruglio of the University of Padova suggested in 2017 that neutrino masses might be complex analytic functions called modular forms. The starting point of this novel idea is that non-Abelian discrete family symmetries may arise from superstring theory in compactified extra dimensions, as a finite subgroup of the modular symmetry of such theories (i.e. the symmetry associated with the non-unique choice of basis vectors spanning a given extra-dimensional lattice). It follows that the 4D effective Lagrangian must respect modular symmetry. This, Feruglio observed, implies that Yukawa couplings may be modular forms. So if the leptons transform as triplets under some finite subgroup of the modular symmetry, then the Yukawa couplings themselves must transform also as triplets, but with a well defined structure depending on only one free parameter: the complex modulus field. At a stroke, this removes the need for flavon fields and ad hoc vacuum alignments to break the family symmetry, and potentially greatly simplifies the particle content of the theory.

Compactification

Although this approach is currently actively being considered, it is still unclear to what extent it may shed light on the entire flavour problem including all quark and lepton mass hierarchies. Alternative string-theory motivated ideas for addressing the flavour problem are also being developed, including the idea that flavons can arise from the components of extra-dimensional gauge fields and that their vacuum alignment may be achieved as a consequence of the compactification mechanism.

The discovery of neutrino mass and mixing makes the flavour puzzle hard to ignore

Recently, there have been some experimental observations concerning charged lepton flavour universality violation which hint that the flavour scale might not be associated with the GUT scale, but might instead be just around the corner at the TeV scale (CERN Courier May/June 2019 p33). Recall that in the SM the charged leptons e, μ and τ interact identically with the gauge forces, and differ only in their masses, which result from having different Yukawa couplings to the Higgs doublet. This charged lepton flavour universality has been the subject of intense experimental scrutiny over the years and has passed all the tests – until now. In recent years, anomalies have appeared associated with violations of charged lepton flavour universality in the final states associated with the quark transitions b → c and b → s.

Puzzle solving

In the case of b → c transitions, the final states involving τ leptons appear to violate charged lepton universality. In particular B → D^(*) ℓ ν_ℓ decays where the charged lepton ℓ is identified with τ have been shown by Babar and LHCb to occur at rates somewhat higher than those predicted by the SM (the ratios of such final states to those involving electrons and muons being denoted by R_D and R_D*). This is quite puzzling since all three types of charged leptons are predicted to couple to the W boson equally, and the decay is dominated by tree-level W exchange. Any new-physics contribution, such as the exchange of a new charged Higgs boson, a new W′ or a leptoquark, would have to compete with tree-level W exchange. However, the most recent measurements by Belle, reported at the beginning of 2019 (CERN Courier May/June 2019 p9), measure R_D and R_D* to be closer to the SM prediction.

In the case of b → s transitions, the LHCb collaboration and other experiments have reported a number of anomalies in B → K^(*) ℓ⁺ℓ^– decays such as the R_K and R_K* ratios of final states containing μ⁺μ^– versus e⁺e^–, which are measured deviate from the SM by about 2.5 standard deviations. Such anomalies, if they persist, may be accounted for by a new contact operator coupling the four fermions b_Ls_Lμ_Lμ_L suppressed by a dimensionful coefficient M²_new  where M_new ~30 TeV, according to a general operator analysis. This hints that there may be new physics arising from the non-universal couplings of leptoquark and/or a new Z′ whose mass is typically a few TeV in order to generate such an operator (where the 30 TeV scale is reduced to just a few TeV after mixing angles are taken into account). However, the introduction of these new particles increases the SM parameter count still further, and only serves to make the flavour problem of the SM worse.

Link-up

Motivated by such considerations, it is tempting to speculate that these recent empirical hints of flavour non-universality may be linked to a possible theory of flavour. Several authors have hinted at such a connection, for example Riccardo Barbieri of Scuola Normale Superiore, Pisa, and collaborators have related these observations to a U(2)⁵ flavour symmetry in an effective theory framework. In addition, concrete models have recently been constructed that directly relate the effective Yukawa couplings to the effective leptoquark and/or Z′ couplings. In such models the scale of new physics associated with the mass of the leptoquark and/or a new Z′ may be identified with the flavour scale M_fl defined earlier, except that it should be not too far from the TeV scale in order to explain the anomalies. To achieve the desired link, the effective leptoquark and/or Z′ couplings may be generated by the same kinds of operators responsible for the effective Higgs Yukawa couplings (figure 3).

In such a model the couplings of leptoquarks and/or Z′ bosons may be related to the Higgs Yukawa couplings, with all couplings arising effectively from mixing with a vector-like fourth family. The considered model predicts, apart from the TeV scale leptoquark and/or Z′, and a slightly heavier fourth family, extra flavour-changing processes such as τ → μμμ. The model in its current form does not have any family symmetry, and explains the hierarchy of the quark masses in terms of the vector-like fourth family masses, which are free parameters. Crucially, the required TeV scale Z′ mass is given by M_Z′ ~ <φ> ~ TeV, which would fix the flavour scale M_fl ~ few TeV. In other words, if the hints for flavour anomalies hold up as further data are collected by the LHCb, Belle II and other experiments, the origin of flavour may be right around the corner.