The W and Z at LEP

The Large Electron Positron collider made significant contributions to the process of establishing the Standard Model as the basis for matter and forces, and also built a platform for physics scenarios beyond the model.

The Standard Model of particle physics is arguably one of the greatest achievements in physics in the 20th century. Within this framework the electroweak interactions, as introduced by Sheldon Glashow, Abdus Salam and Steven Weinberg, are formulated as an SU(2) x U(1) gauge field theory with the masses of the fundamental particles generated by the Higgs mechanism. Both of the first two crucial steps in establishing experimentally the electroweak part of the Standard Model occurred at CERN. These were the discovery of neutral currents in neutrino scattering by the Gargamelle collaboration in 1973, and only a decade later the discovery by the UA1 and UA2 collaborations of the W and Z gauge bosons in proton-antiproton collisions at the converted Super Proton Synchrotron.

cernlep1_5-04 — Fig. 1. The cover page (left) of the seminal CERN yellow report 76-18 on the physics potential of a 200 GeV e⁺e^– collider, and the eventual facility as realized in LEP at CERN (top), including the four universal detectors ALEPH, DELPHI, L3 and OPAL.

Establishing the theory at the quantum level was the next logical step, following the pioneering theoretical work of Gerard ‘t Hooft and Martinus Veltman. Such experimental proof is a necessary requirement for a theory describing phenomena in the microscopic world. At the same time, performing experimental analyses with high precision also opens windows to new physics phenomena at much higher energy scales, which can be accessed indirectly through virtual effects. These goals were achieved at the Large Electron Positron (LEP) collider.

cernlep2_5-04 — Fig. 2. Typical events recorded in the four LEP experiments: (a) µ⁺µ^– pair at OPAL; (b) τ⁺τ^– pair at DELPHI; (c) three-jet event at L3; and (d) W⁺W^– event at ALEPH.

LEP also provided indirect evidence for the fourth step in this process, establishing the Higgs mechanism for generating mass. However, the final word on this must await experimentation in the near future at the Large Hadron Collider.

The beginnings of LEP

Before LEP started operating in 1989, the state of the electroweak sector could be described by a small set of characteristic parameters. The masses of the W and Z bosons had been measured to an accuracy of a few hundred MeV, and the electroweak mixing parameter sin²θ_W had been determined at the percent level. This accuracy allowed the top-quark mass to be predicted at 130 ± 50 GeV, but no bound could be derived on the Higgs mass.

The idea of building such an e⁺e^– collider in the energy region up to 200 GeV was put forward soon after the first highly successful operation of smaller machines in the early 1970s at energies of a few GeV. The physics potential of such a high-energy facility was outlined in a seminal CERN yellow report (figure 1).

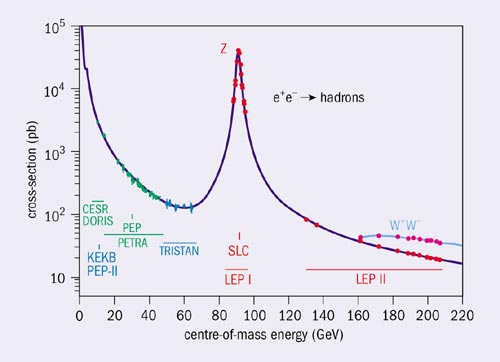
cernlep3_5-04 — Fig. 3. The e⁺e^– annihilation cross-section to hadrons, from initial low energies in early colliders to the maximum energy at LEP.

LEP finally started operation in 1989, equipped with four universal detectors, ALEPH, DELPHI, L3 and OPAL. The machine operated in two phases. In the first phase, between 1989 and 1995, 18 million Z bosons were collected, while in the second phase, from 1996 to 2000, some 80,000 W bosons were generated at energies gradually climbing from the W-pair threshold to the maximum of 209 GeV. The machine performance was excellent at all the energy steps.

Phase I: Z physics

The Z boson in the Glashow-Salam-Weinberg model is a mixture of the neutral isospin SU(2) and the hypercharge U(1) gauge fields, with the mixing parameterized by sin²θ_W. The Z boson interacts with vector and axial-vector currents of matter. The Z-matter couplings, including the mixing angle, are affected by radiative corrections so that high-precision analyses allow both tests at the quantum level and extrapolations to new scales of virtual particles.

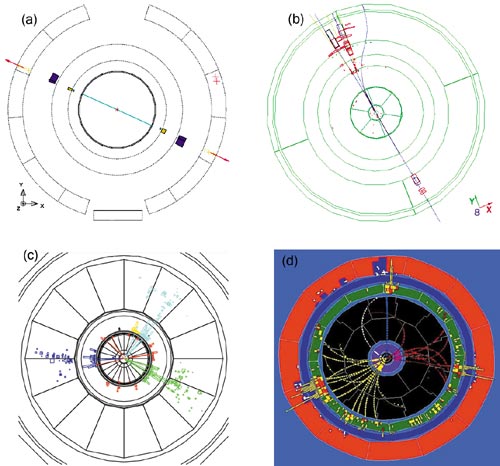
The properties of the Z boson and the underlying electroweak theory were studied at LEP by measuring the overall formation cross-section, the forward-backward asymmetries of the leptons and quarks, and the polarization of tau leptons. Outstandingly clear events were observed in each of the four detectors (see figure 2). As a result, the experimental analyses of the Z line-shape (see figure 3) of the decay branching ratios and the asymmetries were performed with a precision unprecedented in high-energy experiments (see equation 1 for all Z data, including SLD).

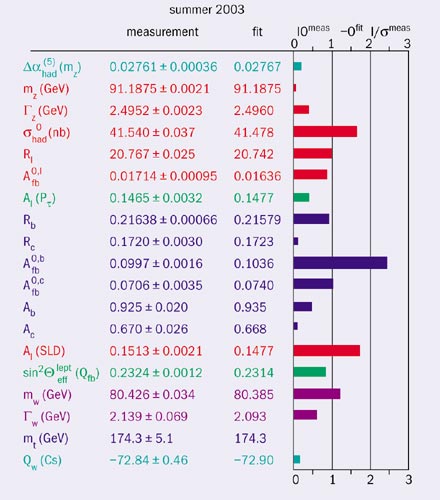
Thus, the electroweak sector of the Standard Model successfully passed the examination at the per-mille level, as highlighted by global analysis of the electroweak mixing parameter sin²θ_W. This is truly in the realm where quantum theory is the proper framework for formulating the laws of nature. Figure 4 shows the observables that were precisely measured at LEP. The picture is uniform in all the observables, with deviations from the average line a little above and below 2σ only in the forward-backward asymmetry of the b-quark jets, and the left-right polarization asymmetry measured at the Stanford Linear Collider facility.

However, beyond this most stringent test of the electroweak theory itself, Z physics at LEP allowed important conclusions to be drawn on several other aspects of the Standard Model and potential physics beyond.

cernlep5_5-04 — Fig. 4. Precision observables of the electroweak part of the Standard Model, measured at LEP and elsewhere.

The first of these concerned the three families of leptons in the Standard Model. The number of light neutrinos could be determined by comparing the Z width as measured in the Breit-Wigner line-shape with the visible lepton and quark-decay channels. The ensuing difference determines the number of light neutrino species to be three: N_ν = 2.985 ± 0.008. Thus, LEP put the lid on the Standard Model with three families of matter particles.

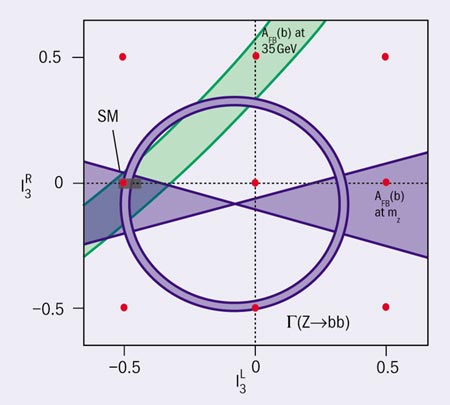
The physics of the top quark was another real success story at LEP. Not only could the existence of this heaviest of all quarks be predicted from LEP data, but the mass could also be pre-determined with amazing accuracy from the analysis of quantum corrections – a textbook example of the fruitful co-operation of theory and experiment. By analysing rate and angular asymmetries in Z decays to b-quark jets at LEP and complementing this set with production rates at the lower energy collider PETRA, the isospin of the b-quark could be uniquely determined (figure 5). From the quantum number I₃^L = -1/2, the existence of an isospin +1/2 partner to the bottom quark could be derived conclusively – in other words, the top quark.

cernlep6_5-04 — Fig. 5. Determining the weak isospin of the bottom quark. The blue circle represents the partial Z decay width to bbbar pairs at LEP; blue wedges are the forward-backward asymmetry at LEP; and the green strip is the cross-section at PETRA. All measurements cross the point [I³_L, I³_R] = [-1/2, 0], so an isospin partner to the b-quark with [I³_L, I³_R] = [+1/2, 0] should exist, i.e. the top quark.

There was more than this, however. Virtual top quarks affect the masses and the couplings of the electroweak gauge bosons, in particular the relation between the Fermi coupling G_F of beta decay, the Sommerfeld fine-structure constant α, the electroweak mixing sin²θ_W and the mass of the Z boson, M_Z. This correction is parameterized in the ρ parameter and increases quadratically in the top-quark mass: Δρ ~ G_Fm_t². This led to the prediction of m_t = 173 ⁺¹²_-13 ⁺¹⁸_-20 GeV, before top quarks were established at the Tevatron and their mass confirmed by direct observation. This was truly a triumph of high-precision experimentation at LEP coupled with theoretical high-precision calculations at the quantum level of the Standard Model.

Beyond the electroweak sector

Z physics at LEP has also contributed to our knowledge of quantum chromodynamics (QCD), the theory of strong interactions in the complete SU(3) x SU(2) x U(1) Standard Model. As was already apparent from the study of PETRA jets at DESY, the clean environment of electron-positron collisions enables these machines to be used as precision tools for studying QCD. At LEP several remarkable observations contributed to putting QCD on a firm experimental basis.

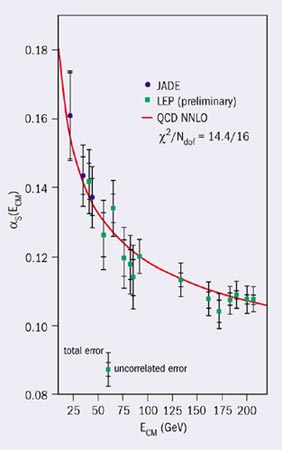
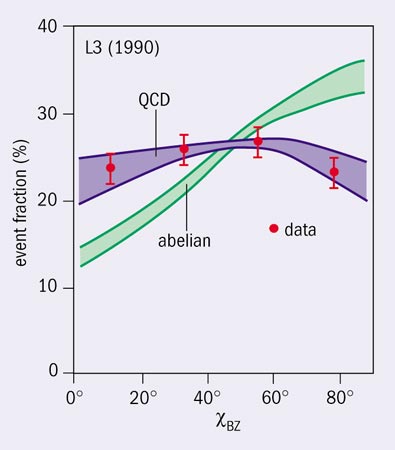
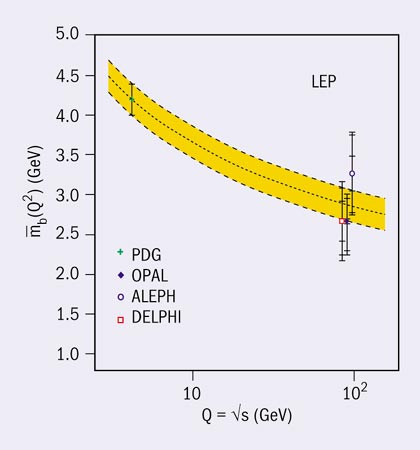
Firstly, with the measurement of the QCD coupling α_s = 0.1183 ± 0.0027 at the scale M_Z and the jet analysis of the running from low energies at PETRA to high energies at LEP, the validity of asymptotic freedom could be demonstrated in a wonderful way (see figure 6a). Secondly, the observation of the three-gluon self-coupling in four-jet final states of Z-boson decays enabled QCD to be established as a non-abelian gauge theory (see figure 6b). With the measured value C_A = 3.02 ± 0.55, the strength of the three-gluon coupling agrees with the predicted value C_A = 3 for non-abelian SU(3), and is far from the value of zero in any abelian “QED type” field theory without self-coupling of the gauge bosons. Thirdly, in the same way as couplings run, quark masses change when weighed at different energy scales, induced by the retarded motion of the surrounding gluon cloud. This effect was observed in a unique way by measuring the b-quark mass at the Z scale (see figure 6c).

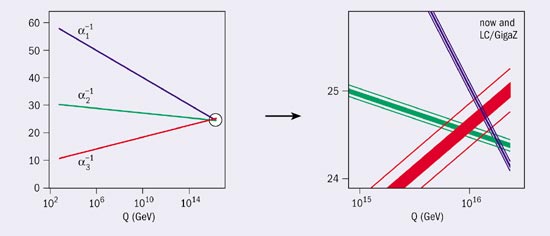
There is one further triumph of the Z-physics programme. When extrapolating the three couplings associated with the gauge symmetries SU(3) x SU(2) x U(1) in the Standard Model to high energies, they approach each other but do not really meet at the same point. This is different if the particle spectrum of the Standard Model is extended by supersymmetric partners. Independently of the mass values, so long as they are in the TeV region, the new degrees of freedom provided by supersymmetry make the couplings converge to an accuracy close to 2% (see figure 7). This opens up the exciting vista that the electromagnetic, weak and strong forces of the Standard Model may be unified at an energy scale close to 10¹⁶ GeV, while at the same time giving support to supersymmetry, a symmetry that may be intimately related to gravity, the fourth of the forces we observe in nature.

cernlep8_5-04 — Fig. 6. (a) The running of the QCD coupling from low PETRA to high LEP energies compared with the prediction of asymptotic freedom.

Phase II: W physics

Gauge field theories appear to be the theoretical framework within which the three fundamental particle forces can be understood. The gauge symmetry theory was introduced by Hermann Weyl as the basic symmetry principle of quantum electrodynamics; the scheme was later generalized by C N Yang and R L Mills to non-abelian gauge symmetries, before being recognized as the basis of the (electro) weak and strong interactions.

One of the central tasks of the LEP experiments at energies beyond the W-pair threshold was the analysis of the electroweak three-gauge-boson couplings, predicted in form and magnitude by the gauge symmetry. A first glimpse was also caught of the corresponding four-boson couplings.

cernlep9_5-04 — Fig. 6. (b) The distribution of the azimuthal angle between the planes spanned by the high-energy jets and the low-energy jets in four-jet events. The experimental distribution is compatible with QCD, involving the self-couplings of the gluons, but it cannot be reproduced by an abelian “QED type” field theory of the strong interactions without gauge-boson self-coupling.

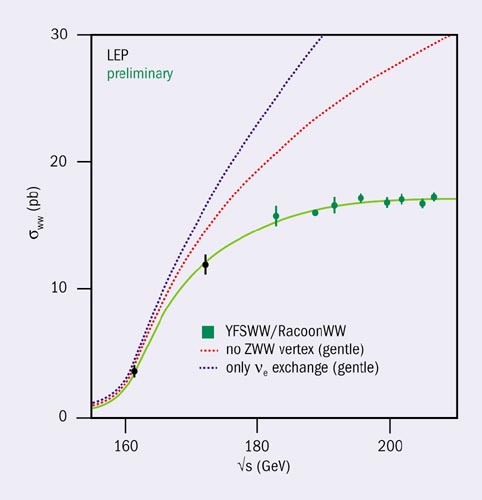
Charged W⁺W^– pairs are produced in e⁺e^– collisions by three different mechanisms: neutrino exchange, and photon- and Z-boson exchanges. From the steep increase of the excitation curve near the threshold and from the reconstruction of the W bosons in the leptonic and hadronic decay modes, the mass M_W and the width Γ_W can be reconstructed with high precision (see equation 2).

This value of the directly measured W mass is in excellent agreement with the value extracted indirectly from radiative corrections.

Any of the three production mechanisms for W⁺W^– pairs, if evaluated separately, leads to a cross-section that rises indefinitely with energy. However, the amplitudes interfere destructively as a result of the gauge symmetry, and the final cross-section is damped for large energies. The prediction of gauge cancellations is clearly borne out by the LEP data (see figure 8), thus confirming the crucial impact of gauge symmetries on the dynamics of the electroweak Standard Model sector in a most impressive way.

cernlep10_5-04 — Fig. 6. (c) The change in the bottom-quark mass when weighed at low and high energies.

The role of the gauge symmetries can be quantified by measuring the static electroweak parameters of the charged W bosons, i.e. the monopole charges (g_W), the magnetic dipole moments (µ_W) and the electric quadrupole moments (q_W) of the W bosons coupled to the photon and Z boson. For the photon coupling g_W = e, µ_W = 2 x e/2M_W, q_W = -e/M_W² and for the Z coupling analogously. These predictions have been confirmed experimentally within a margin of a few percent.

Studying the quattro-linear couplings requires three-boson final states. Some first analyses of W⁺W^–γ final states bounded any anomalies to less than a few percent.

Hunting the Higgs

cernlep11_5-04 — Fig. 7. The extrapolation of the SU(3), SU(2) and U(1) gauge couplings to high energies in the minimal supersymmetric extension of the Standard Model; they approach each other near 2 x 10¹⁶ GeV at a level of 2% – indicative of the grand unification of the three-gauge interactions.

The fourth step in establishing the Standard Model experimentally – the search for the Higgs particle – could not be completed by LEP. Nevertheless, two important results could be reported by the experiments. The first of these was to estimate the mass of the Higgs when acting as a virtual particle. By emitting and reabsorbing a virtual Higgs boson, the masses of electroweak bosons are slightly shifted. In parallel to the top quark, this effect can be included in the ρ parameter. With Δρ ~ G_FM_W²logM_H²/M_W², the effect is however only logarithmic in the Higgs mass, so that the sensitivity is reduced considerably. Nevertheless, from the celebrated “blue-band plot”, a most probable value of about 100 GeV in the Standard Model, though with large error, is indicated by evaluating the entire set of established precision data (see figure 9). An upper bound close to 200 GeV has been found in the analysis shown in equation 3a.

cernlep12_5-04 — Fig. 8. The total cross-section for W-pair production e⁺e^–→W⁺W^– at LEP in the Standard Model. The measurements are also confronted with *ad hoc* calculations in which three-boson self-couplings are switched off. The gauge symmetries are apparently crucial for the understanding of the measurements.

Thus, in the framework of the Standard Model and a large class of possible extensions, LEP data point to a Higgs mass in the moderately small, intermediate mass range. This is corroborated by individual analyses of all the observables, except the forward-backward asymmetry of b-jets. (This indirect evidence for a light Higgs sector is complemented by indirect counter-evidence against a large class of models constructed for generating mechanisms of electroweak symmetry breaking by new strong interactions.)

The direct search for the real production of the Higgs particle at LEP through the “Higgs-strahlung” process, e⁺e^–→ZH, set a stringent lower limit on the mass of the particle in the Standard Model (see equation 3b).

However, we have been left with a 1.7σ effect for Higgs masses in excess of 115 GeV, fuelled by the four-jet channel in one experiment. “This deviation, although of low significance, is compatible with a Standard Model Higgs boson in this mass range, while also being in agreement with the background hypothesis.” (LEP Higgs Working Group.)

LEP’s legacy

Based on the high-precision measurements by the four experiments, ALEPH, DELPHI, L3 and OPAL, and in coherent action with a complex corpus of theoretical analyses, LEP achieved an impressive set of fundamental results, the traces of which will be imprinted in the history of physics. LEP firmly established essential elements of the Standard Model at the quantum level. It provided indirect evidence for the existence of a light Higgs boson of the type required by the Standard Model. The extrapolations of the three gauge couplings measured at LEP point to the grand unification of the individual gauge interactions at a high-energy scale – compatible with the supersymmetric extension of the Standard Model in the TeV range.

cernlep15_5-04 — Fig. 9. Probability of the Higgs-mass value in the Standard Model as extracted from radiative corrections to electroweak precision data (maximum probability at minimum of the band). The yellow region is excluded by the (unsuccessful) direct search for the Higgs boson at LEP.

In addition, the precision analyses performed at LEP probed the many physics scenarios beyond the Standard Model, constraining their parameters in the ranges between the upper LEP energy to the TeV and multi-TeV scales. These studies have led to a large number of bounds on masses of supersymmetric particles, masses and mixings of novel heavy gauge bosons, scales of extra space-time dimensions, radii of leptons and quarks, and many other examples.

•The figures and the experimental numbers are from the four LEP experiments, the LEP Electroweak Working Group, the LEP Higgs Working Group, G Altarelli, S Bethke, D Haidt, W Porod, D Schaile and R Seuster.

This article is based on a talk given by Peter Zerwas at the symposium held at CERN in September 2003 entitled “1973: neutral currents, 1983: W^± and Z⁰ bosons. The anniversary of CERN’s discoveries and a look into the future.” The full proceedings will be published as volume 34 issue 1 of The European Physical Journal C. Hardback ISBN: 3540207503.