H1 and ZEUS release their definitive paper on deep-inelastic scattering.
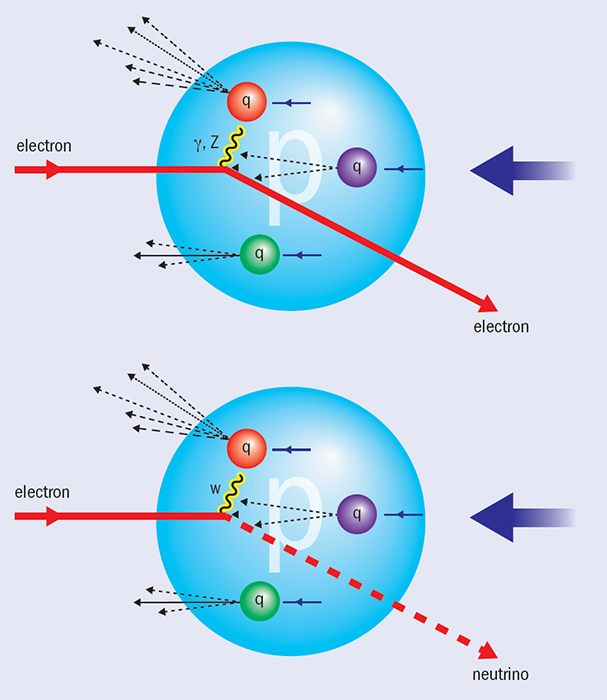
Image credit: DESY.
After 15 years of measurement and another eight years of scrutinizing and calculations, the H1 and ZEUS collaborations have published the most precise results to date about the innermost structure and behaviour of the proton. The two collaborations, which took data at DESY’s electron–proton collider, HERA, from 1992 to 2007, have combined nearly 3000 measurements of inclusive deep-inelastic cross-sections (H1, ZEUS 2015). With its completion, the paper secures the legacy of the HERA data.
Within the framework of perturbative QCD, the proton is described in terms of parton-density functions, which provide the probability of scattering from a parton, either a gluon or a quark. The H1 and ZEUS collaborations have also produced the first QCD analysis of the data, encompassed in the HERAPDF2.0 sets of parton-distribution functions (PDFs), which form a significant part of the paper. The combined data presented in the new publication will be the basis of all analyses of the structure of the proton for years to come.
As figure 1 depicts, in deep-inelastic scattering, a boson – γ, Z0 or W± – acts as a probe of the structure of the proton by interacting with its constituents, through neutral-current (γ, Z0) or charged-current (W±) reactions. Of course, this picture is simplified: the proton is a dynamic structure of quarks and gluons, but by measuring deep-inelastic scattering over a wide kinematic range, this internal structure can be mapped precisely. The variables used to do this are the squared four-momentum, Q2, of the exchanged boson, and Bjorken x, xBj, the fraction of the proton’s momentum carried by the struck quark.
A wealth of data
The data, taken over the 15-year lifetime of the HERA accelerator, correspond to a total luminosity of about 1 fb–1 of deep-inelastic electron–proton and positron–proton scattering. All of the data used were taken with an electron/positron beam energy of 27.5 GeV, with roughly equal amounts of data for electron–proton and positron–proton scattering being recorded. HERA initially operated with a proton-beam energy of 820 GeV, which was increased subsequently to 920 GeV; these data constitute the bulk of the combined measurements. Towards the end of HERA’s run, special data samples with a proton-beam energy of 575 GeV and 460 GeV were taken and are also included. The data were combined separately for the e+p and e–p runs and for the different centre-of-mass energies. Overall, 41 separate data sets were used in the combination, spanning 0.045 < Q2 < 50,000 GeV2 and 6 × 10–7 < xBj < 0.65, i.e. six orders of magnitude in each variable. The initial measurements consisted of 2937 published cross-sections in total, which were combined to produce 1307 final combined cross-section measurements. These results supersede the previous paper with combined measurements of deep-inelastic scattering cross-sections in which only data up to the year 2000 were combined (CERN Courier January/February 2008 p30).

The procedure for combining the data involved a careful treatment of the various uncertainties between all of the data sets. In particular, the correlations of the various sources were assessed, and those uncertainties deemed to be point-to-point correlated were accounted for as such in the averaging of the data based on a χ2 minimization method. The resulting χ2 is 1687 for 1620 degrees of freedom, demonstrating excellent compatibility of the multitude of data sets. Figure 2 illustrates the power of the data combination. It displays a selection of the data in bins of the photon virtuality, Q2, and for fixed values of xBj, showing separately individual data sets from several different analyses. A combined data point can be the combination of up to eight individual measurements. The improvement in precision is striking, as is seen more clearly in the close-up on some of the points. An indication of the precision of the combined data is that the total uncertainties are close to 1% for the bulk region of 3 < Q2 < 500 GeV2.
As well as showing the precision of the data and power of the combination, the cross-section dependence for the different values of xBj demonstrates the dynamic structure of the proton in a striking way. For xBj = 0.08, the cross-section dependence is reasonably flat as a function of Q2. This is known as Bjorken scaling, and is expected from the simple parton model in which inelastic electron–proton scattering is viewed as a sum of elastic electron–parton scattering, where the partons are free point-like objects. At lower values of xBj, the cross-section rises increasingly more steeply with increasing Q2 and decreasing xBj. This effect is known as scaling violation, and is indicative of the density of gluons in the proton increasing.
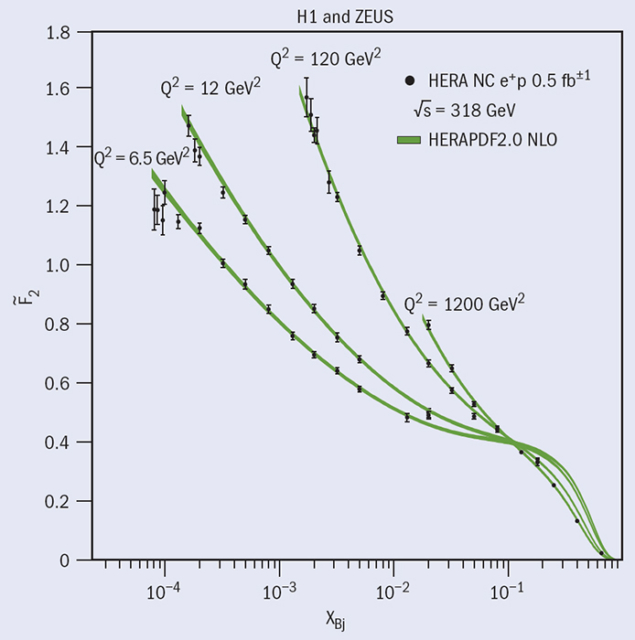
The increased density and rise of the cross-section can also be observed by considering the proton-structure function F2 (which is closely related to the cross-section) plotted versus xBj at fixed Q2, as in figure 3. The strong rise of F2 with decreasing xBj was one of the most important discoveries at HERA. Previous experiments, which were with fixed targets, could not constrain this behaviour, because the data were at low values of Q2 and high values of xBj. The figure also shows how the rise towards low xBj is steeper with increasing Q2. At higher Q2, the exchanged boson effectively probes smaller distances, and so can see more of the inner structure of the proton and hence resolves more and more gluons.
Parton distributions
The proton structure of quarks and gluons is often parameterized in terms of the PDFs, which correspond to the probability of finding a gluon or a quark of a given flavour with momentum fraction x in the proton, given the scale μ of the hard interaction. The behaviour of the PDFs with scale is predicted by QCD, but the absolute values need to be determined from fits to data. Using the HERA data, the PDFs can be extracted, while at the same time the evolution as a function of the scale is tested. This analysis is performed at leading order, next-to-leading order (NLO) and next-to-next-to-leading order, yielding the HERAPDF2.0 family of PDFs.
Figure 3 compares the predictions of the PDF analysis at NLO with the measurements of the structure functions. In general, the QCD predictions describe the data well, although this becomes poorer at low Q2, indicating inadequacies in the theory used at these low scales. Such precise knowledge of the PDFs is also of highest importance for physics at the LHC at CERN, because the uncertainties stemming from the knowledge of the PDFs are increased for proton–proton collisions compared with deep-inelastic scattering.
The QCD analysis can also be extended to include data from the production of charm quarks and jets at HERA. Charm production is measured again as a function of xBj and Q2, however with the condition of detecting a charm meson in the final state. Jet production is measured in the Breit frame, where jets with non-zero transverse momentum are expected from hard QCD processes only. By including the charm and jet data, the analysis becomes particularly sensitive to the strong-coupling constant, αs(MZ), whereas without jet data the coupling constant is strongly correlated with the normalization of the gluon density. The combined analysis of inclusive data, charm data and jet data at NLO results in an experimentally very precise measurement of the strong-coupling constant, αs(MZ) = 0.1183±0.0009 (exp.), with significantly larger uncertainties of +0.0039–0.0033 related to the model and theory.
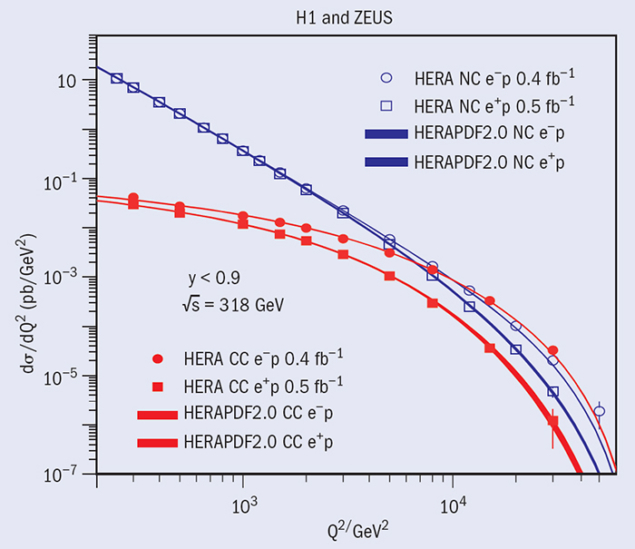
It is also interesting to look at data from HERA on neutral-current (NC) and charged-current (CC) scattering that is differential in Q2 but integrated over xBj, as shown in figure 4 both for e+p and e–p. At small Q2, the cross-sections for NC are much larger than for CC, whereas at large Q2, in the order of the vector-boson mass squared, they become similar in size. This is a direct visualization of the electroweak unification: the CC process is mediated by weak forces, whereas photon exchange dominates the NC cross-section. Looking in more detail, the NC cross-sections for e+p and e–p are almost identical at small Q2 but start to diverge as Q2 grows. This is owing to γ–Z0 interference, which has the opposite effect on the e+p and e–p cross-sections. The CC cross-sections also differ between e+p and e–p scattering, with two effects contributing: the helicity structure of the W± exchange and the fact that CC e–p scattering probes the u-valence quarks, whereas d-valence quarks are accessed in CC e+p.
In summary, the HERA collider experiments H1 and ZEUS have combined their precision data on deep-inelastic scattering, reaching a precision of almost 1% in the double-differential cross-section measurements. It is the largest coherent data set on proton structure, spanning six orders of magnitude in the kinematic variables xBj and Q2. A QCD analysis of the HERA data alone results in a set of parton-density functions, HERAPDF2.0, without the need for data from other experiments. Also, using HERA jet and charm data, the strong-coupling constant is measured together with proton PDFs. QCD and electroweak effects are probed at high precision in the same data set, providing beautiful demonstrations of the validity of the Standard Model.





