A research group at KEK has succeeded in calculating the state inside a black hole using computer simulations based on superstring theory. The calculations confirmed for the first time that the temperature dependence of the energy inside a black hole agrees with the power-law behaviour expected from calculations based on Stephen Hawking’s theory of black-hole radiation. The result demonstrates that the behaviour of elementary particles as a collection of strings in superstring theory can explain thermodynamical properties of black holes.

Image credit: KEK.
In 1974, Stephen Hawking at Cambridge showed theoretically that black holes are not entirely black. A black hole in fact emits light and particles from its surface, so that it shrinks little by little. Since then, physicists have suspected that black holes should have a certain interior structure, but they have been unable to describe the state inside a black hole using general relativity, as the curvature of space–time becomes so large towards the centre of the hole that quantum effects make the theory no longer applicable. Superstring theory, however, offers the possibility of bringing together general relativity and quantum mechanics in a consistent manner, so many theoretical physicists have been investigating whether this theory can describe the interior of a black hole.
Jun Nishimura and colleagues at KEK established a method that efficiently treats the oscillation of elementary strings depending on their frequency. They used the Hitachi SR11000 model K1 supercomputer installed at KEK in March 2006 to calculate the thermodynamical behaviour of the collection of strings inside a black hole. The results showed that as the temperature decreased, the simulation reproduced behaviour of a black hole as predicted by Hawking’s theory (figure 1).
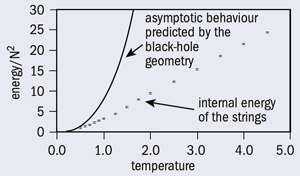
This demonstrates that the mysterious thermodynamical properties of black holes can be explained by a collection of strings fluctuating inside. The result also indicates that superstring theory will develop further to play an important role in solving problems such as the evaporation of black holes and the state of the early universe.
Further reading
K N Anagnostopoulos et al. 2008 Phys. Rev. Lett. 100 021601.








