Is it possible to travel faster than light? Can we travel back in time, or send signals into the past? These questions have intrigued physicists since the discovery of special relativity nearly a century ago highlighted the fundamental nature of the speed of light and revolutionized our concept of time. Graham Shore describes recent research that sheds new light on these old questions.
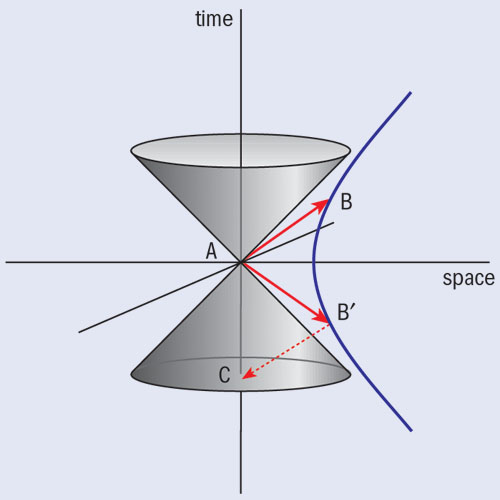
Quantum effects such as vacuum polarization in gravitational fields appear to permit “superluminal” photon propagation and give a fascinating new perspective on our understanding of time and causality in the microworld. To understand these new developments, we first need to question the origin of the received wisdom that superluminal motion necessarily leads to unacceptable causal paradoxes. In special relativity, the problem arises because while all observers agree about the time ordering of events linked by a subluminal signal, for a superluminal signal different observers disagree on whether the signal was received after or before it was emitted. In other words, viewed in a certain class of inertial frames, a superluminal signal travels backwards in time (figure 1). However, by itself this is not sufficient to establish the familiar causal paradoxes associated with time travel. A genuine causal paradox requires a signal to be sent from the emitter to a point in its own past light-cone – a time-reversed return path must also be possible. In special relativity, such a return path is guaranteed by the existence of global inertial frames. Crucially, a causal paradox requires both of these conditions to be met.
This is the loophole that may allow the possibility of superluminal propagation in general relativity. Einstein’s theory of gravity is based on the weak equivalence principle, which states that at each point in space-time there exists a local inertial frame – in other words a freely falling observer does not feel a gravitational force. This principle leads directly to the description of gravity by a curved space-time that is locally flat. In the conventional theory, however, this is supplemented by a further simplifying assumption, known as the strong equivalence principle (SEP), which requires that dynamical laws are the same in each of these local inertial frames.
While the SEP may be consistently imposed in classical physics, somewhat surprisingly it is violated in quantum theory (see Further information). In quantum electrodynamics (QED), Feynman diagrams involving a virtual electron-positron pair influence the photon propagator. This gives the photon an effective size of the order of the Compton wavelength of the electron. If the space-time curvature has a comparable scale, then an effective photon-gravity interaction is induced. This depends explicitly on the curvature, in violation of the SEP. The photon velocity is changed and light no longer follows the shortest possible path. Moreover, if the space-time is anisotropic, this change can depend on the photon’s polarization as well as direction. This is the quantum phenomenon of “gravitational birefringence”. The effective light-cones for the propagation of photons in gravitational fields no longer coincide with the geometrical light-cones fixed by the local Lorentz invariance of space-time, but depend explicitly on the local curvature.
Superluminal photons
Drummond and Hathrell first described this phenomenon in a seminal paper in 1980. But a further surprise was in store. When they computed the quantum modifications to the light-cones, they found that in many cases the photon velocity was superluminal. Indeed we now know that for propagation in vacuum space-times (solutions of Einstein’s field equations in regions with no matter present, such as the neighbourhood of the event horizon of black holes), there is a general theorem showing that if one photon polarization has a conventional subluminal velocity, the other polarization is necessarily superluminal. In fact, gravity affects the photon velocity in two distinct ways: the first through the energy momentum of the gravitating matter; and the second through the component of the curvature of space-time that is not determined locally by matter, the so-called Weyl curvature. It is this that produces birefringence.
Can superluminal photon propagation really be compatible with the principle of causality, or does it necessarily imply the existence of time machines? After all, such motion is genuinely backwards in time as viewed locally by a class of inertial observers. The question remains controversial, but the key is the SEP. In special relativity, a causal paradox requires both outward and return signals to be backwards in time in a global inertial frame. In general relativity, however, global Lorentz invariance is lost and the existence of a sufficiently superluminal return signal is not guaranteed. The quantum violation of the SEP certainly permits superluminal motion, but with photon velocities predetermined by the local curvature. Consistency with causality is therefore a global question. If the original space-time admits a global causal structure with respect to the geometrical light-cones, then causality will be respected even in the presence of superluminal photons if this structure is preserved with respect to the new light-cones. This rapidly leads to sophisticated issues of global topology in general relativity, but at this stage superluminal photons appear to be both consistent with causality and predicted by QED.
Black holes and cosmology
Since the original Drummond-Hathrell discovery, superluminal photons have been studied in a variety of curved space-times, ranging from the Schwarzschild, Reissner-Nordström or Kerr metrics describing black holes to the Bondi-Sachs space-time describing gravitational radiation from an isolated source and the Friedmann-Robertson-Walker (FRW) space-time of Big Bang cosmology. One of the most fascinating results to emerge involves the status of the event horizon surrounding a black hole. At first sight, it seems that if we can exceed the usual speed of light, it may be possible to escape from within the black hole horizon. If so, the location of the effective horizon would become fuzzy on a microscopic scale, with potentially far-reaching consequences for the quantum theory of black holes. Remarkably, however, it turns out that this possibility is not realized – while the light-cones of physical photons may differ from the geometrical light-cones everywhere else, they coincide exactly on the event horizon. Once again, the superluminal phenomenon evades a potentially paradoxical clash with the causal properties of space-time.
Another fascinating result involves the propagation of photons in the very early universe. Investigations of superluminal photons in the FRW space-time show that photon velocity increases rapidly at early times, independently of polarization. Recent work on the rather different subject of cosmologies in which the fundamental constant c varies over cosmological time has shown that an increase in the speed of light in the early universe can resolve the so-called “horizon problem”, which motivates the popular inflationary model of cosmology. Quantitative predictions of the size of quantum-induced superluminal photon velocities in the strong gravitational fields characterizing the inflationary epoch are currently beyond reach, but it is intriguing to reflect that quantum theory predicts that the physical speed of light increased sharply in the very early evolution of the universe.
Gravitational rainbow
The most recent research into superluminal photon propagation in QED has focused on the key issue of dispersion. In conventional optics, light passing through a refractive medium has a reduced phase velocity that depends on its frequency. This dispersive effect allows the group velocity of a wave pulse to differ from its phase velocity, and to be significantly greater or less than c. This is the origin of several striking recent experiments on the speed of light, notably those of Vestergaard Hau and colleagues at Harvard in which they reduce the group velocity of a light pulse almost to zero by shining tuned lasers on a cloud of ultracold sodium atoms.
For fundamental questions relating to causality, however, the relevant “speed of light” is not the group velocity, but the asymptotic value of the phase velocity at high frequency. The original analysis of Drummond and Hathrell determined the phase velocity in the low-frequency limit, so it is of critical importance to extend their work and discover the full dispersion relation for the quantum propagation of photons in a gravitational field. We need to find the frequency dependence of the refractive index for gravity – in other words, the gravitational rainbow. There is, however, a fundamental theorem of conventional optics that requires the refractive index at high frequency to be less than at low frequency. If this remains true in the gravitational context, then the original superluminal prediction would in fact be a lower bound on the crucial asymptotic phase velocity. However, the validity of this theorem in the presence of gravity has been questioned and a final resolution must rely on explicit computations of high-frequency propagation. Significant progress has recently been made, suggesting that the superluminal phenomenon can persist to high frequency, but research is ongoing and further surprises cannot be ruled out.
Gravitational lensing
Theoretical evidence for superluminal phenomena is so far confined to the bizarre quantum microworld where virtual particles interact with a foamy, curved space-time. This is the regime where quantum field theory in curved space-time comes into its own and other phenomena arise that challenge our fundamental assumptions about the laws of nature, such as the famous prediction of Hawking radiation from microscopic black holes. But once the cat is out of the bag, it is hard to squeeze it back in. Once we have established that, in principle, superluminal light is possible and the SEP can be violated without compromising causality, it becomes an urgent question to ask whether nature has chosen to take advantage of this scenario on macroscopic, astrophysical scales. If so, how would we observe violations of the SEP in astronomy?

Gravitational birefringence produces a polarization-dependent shift D f = (f2/R2)f in the Einstein formula for the angle of deflection f = 4M/R of light with closest approach distance R to a spherically-symmetric mass M. This would be seen if f2 were characterized by an as yet unknown large scale rather than the quantum scale lc derived in Further information, and would produce a polarization dependence in the apparent position of the lensed images. Observation of this effect would be direct evidence for gravitational birefringence and imply a violation of the strong equivalence principle on astronomical scales. (Photo: Kavan Ratnatunga, Johns Hopkins University.)
The clearest indication of a modified speed of light would be a change in the classic Einstein formula for the deflection of light by a massive object. This was the original prediction of general relativity that was triumphantly verified by Eddington’s 1919 expedition to Brazil, when the deflection of light from a distant star by the Sun was observed during a solar eclipse. This effect is the origin of gravitational lensing (see Hubble image), which in recent years has been developed into a precise and sophisticated tool in astronomy and is used in searches for dark matter and protogalaxies. Gravitational birefringence on astrophysical scales would show up as polarization dependence in gravitational lensing, with the apparent positions of the lensed images changing with the polarization of the observed light. Polarization dependence in gravitational lensing would therefore be a smoking gun for interactions between light and gravity that violate the SEP, and its discovery would have profound implications for fundamental physics.
Further information

In QED, Feynman diagrams involving a virtual electron-positron pair effectively give the photon a “size” of the order of the Compton wavelength lc of the electron ((a) in diagram). This produces an interaction between the photon and gravity that distorts the photon’s trajectory through curved space-time so that it no longer follows the usual geodesic path ((b) in diagram). This effect changes the light-cones from k2 = 0 to k2 = f1 Tmnkm kn + f2 Cmrnskm kn er es where k and e are the photon’s momentum and polarization. There are two distinct effects – one due to the energy momentum Tmn of matter and a second, polarization-dependent, interaction depending on the Weyl curvature Cmrns of the space-time. The remarkable feature of this formula is that it permits both k2 > 0 and k2 < 0, implying superluminal motion ((c) in diagram). p>
In the low-frequency limit, f1 and f2 are constants of the order of alc2, where a is the fine-structure constant. This determines the magnitude of the photon velocity shifts to be of the order of alc2/L2, where L is a typical curvature scale.
In general, f1 and f2 are functions depending on derivatives of the curvature. Determining their precise form is the subject of current research aimed at a complete determination of the dispersion relation for photon propagation in gravitational fields.
Further reading
I T Drummond and S J Hathrell 1980 Phys. Rev. D22 343.
G M Shore 1996 Nucl. Phys. B460 379.
A D Dolgov and I D Novikov 1998 Phys. Lett. B442 82.
G M Shore 2001 Nucl. Phys. B605 455.





