Putting the Pauli exclusion principle on trial

If we tightly grasp a stone in our hands, we neither expect it to vanish nor leak through our flesh and bones. Our experience is that stone and, more generally, solid matter is stable and impenetrable. Last year marked the 50th anniversary of the demonstration by Freeman Dyson and Andrew Lenard that the stability of matter derives from the Pauli exclusion principle. This principle, for which Wolfgang Pauli received the 1945 Nobel Prize in Physics, is based on ideas so prevalent in fundamental physics that their underpinnings are rarely questioned. Here, we celebrate and reflect on the Pauli principle, and survey the latest experimental efforts to test it.

The exclusion principle (EP), which states that no two fermions can occupy the same quantum state, has been with us for almost a century. In his Nobel lecture, Pauli provided a deep and broad-ranging account of its discovery and its connections to unsolved problems of the newly born quantum theory. In the early 1920s, before Schrödinger’s equation and Heisenberg’s matrix algebra had come along, a young Pauli performed an extraordinary feat when he postulated both the EP and what he called “classically non-describable two-valuedness” – an early hint of the existence of electron spin – to explain the structure of atomic spectra.

At that time the EP met with some resistance and Pauli himself was dubious about the concepts that he had somewhat recklessly introduced. The situation changed significantly after the introduction in 1925 of the electron-spin concept and its identification with Pauli’s two-valuedness, which derived from the empirical ideas of Lande, an initial suggestion by Kronig, and an independent paper by Goudsmit and Uhlenbeck. By introducing the picture of the electron as a small classical sphere with a spin that could point in just two directions, both Kronig, and Goudsmit and Uhlenbeck, were able to compute the fine-structure splitting of atomic hydrogen, although they still missed a critical factor of two. These first steps were followed by the relativistic calculations of Thomas, by the spin calculus of Pauli, and finally, in 1928, by the elegant wave equation of Dirac, which put an end to all resistance against the concept of spin.

However, a theoretical explanation of the EP had to wait for some time. Just before the Second World War, Pauli and Markus Fierz made significant progress toward this goal, followed by the publication in 1940 by Pauli of his seminal paper “The connection between spin and statistics”. This paper showed that (assuming a relativistically invariant form of causality) the spin of a particle determines the commutation relations, i.e. whether fields commute or anticommute, and therefore the statistics that particles obey. The EP for spin-1/2 fermions follows as a corollary of the spin-statistics connection, and the division of particles into fermions and bosons based on their spins is one of the cornerstones of modern physics.

Beguilingly simple

The EP is beguilingly simple to state, and many physicists have tried to skip relativity and find direct proofs that use ordinary quantum mechanics alone – albeit assuming spin, which is a genuinely relativistic concept. Pauli himself was puzzled by the principle, and in his Nobel lecture he noted: “Already in my original paper I stressed the circumstance that I was unable to give a logical reason for the exclusion principle or to deduce it from more general assumptions. I had always the feeling and I still have it today, that this is a deficiency. …The impression that the shadow of some incompleteness fell here on the bright light of success of the new quantum mechanics seems to me unavoidable.” Even Feynman – who usually outshone others with his uncanny intuition – felt frustrated by his inability to come up with a simple, straightforward justification of the EP: “It appears to be one of the few places in physics where there is a rule which can be stated very simply, but for which no one has found a simple and easy explanation… This probably means that we do not have a complete understanding of the fundamental principle involved. For the moment, you will just have to take it as one of the rules of the world.”

Of special interest

After further theoretical studies, which included new proofs of the spin-statistics connection and the introduction of so-called para-statistics by Green, a possible small violation of the EP was first considered by Reines and Sobel in 1974 when they reanalysed an experiment by Goldhaber and Scharff in 1948. The possibility of small violations was refuted theoretically by Amado and Primakoff in 1980, but the topic was revived in 1987. That year, Russian theorist Lev Okun presented a model of violations of the EP in which he considered modified fermionic states which, in addition to the usual vacuum and one-particle state, also include a two-particle state. Okun wrote that “The special place enjoyed by the Pauli principle in modern theoretical physics does not mean that this principle does not require further and exhaustive experimental tests. On the contrary, it is specifically the fundamental nature of the Pauli principle that would make such tests, over the entire periodic table, of special interest.”

Okun’s model, however, ran into difficulties when attempting to construct a reasonable Hamiltonian, first because the Hamiltonian included nonlocal terms and, second, because Okun did not succeed in constructing a relativistic generalisation of the model. Despite this, his paper strongly encouraged experimental tests in atoms. In the same year (1987), Ignatiev and Kuzmin presented an extension of Okun’s model in a strictly non-relativisitic context that was characterised by a “beta parameter” |β| << 1. Not to be confused with the relativistic factor v/c, β is a parameter describing the action of the creation operator on the one-particle state. Using a toy model to illustrate transitions that violate the EP, Ignatiev and Kuzmin deduced that the transition probability for an anomalous two-electron symmetric state is proportional to β²/2, which is still widely used to represent the probability of EP violation.

This non-relativistic approach was criticized by A B Govorkov, who argued that the naive model of Ignatiev and Kuzmin could not be extended to become a fully-fledged quantum field theory. Since causality is an important ingredient in Pauli’s proof of the spin-statistics connection, however, Govorkov’s objections could be bypassed: later in 1987, Oscar Greenberg and Rabindra Mohapatra at the University of Maryland introduced a quantum field theory with continuously deformed commutation relations that led to a violation of causality. The deformation parameter was denoted by the letter q, and the theory was supposed to describe new hypothetical particles called “quons”. However, Govorkov was able to show that even this sleight of hand could not trick quantum field theory into small violations of the EP, demonstrating that the mere existence of antiparticles – again a true relativistic hallmark of quantum field theory – was enough to rule out small violations. The take-home message was that the violation of locality is not enough to break the EP, even “just a little”.

The connection between the intrinsic spin of particles and the statistics that they obey are at the heart of quantum field theory and therefore should be tested. A violation of the EP would be revolutionary. It could be related either to the violation of CPT, or violation of locality or Lorentz invariance, for example. However, we have seen how robust the EP is and how difficult it is to frame a violation within current quantum field theory. Experiments face no lesser difficulties, as noted as early as 1980 by Amado and Primakoff, and there are very few experimental options with which to truly test this tenet of modern physics.

One of the difficulties faced by experiments is that the identicalness of elementary particles implies that Hamiltonians must be invariant with respect to particle exchange, and, as a consequence, they cannot change the symmetry of any given state of multiple identical particles. Even in the case of a mixed symmetry of a many-particle system, there is no physical way to induce a transition to a state of different symmetry. This is the essence of the Messiah–Greenberg superselection rule, which can only be broken if a physical system is open.

Breaking the rules

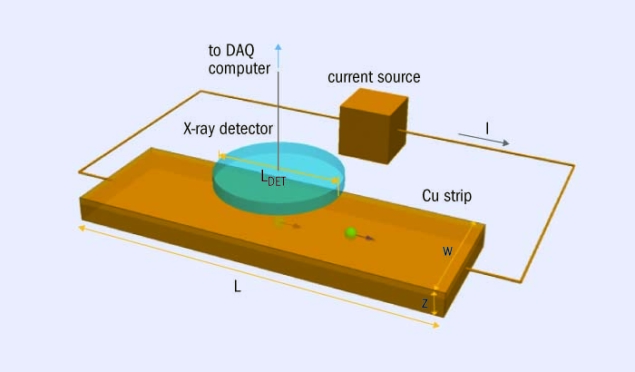
The first dedicated experiment in line with this breaking of the Messiah–Greenberg superselection rule was performed in 1990 by Ramberg and Snow, who searched for Pauli-forbidden X-ray transitions in copper after introducing electrons into the system. The idea is that a power supply injecting an electric current into a copper conductor acts as a source of electrons, which are new to the atoms in the conductor. If these electrons have the “wrong” symmetry they can be radiatively captured into the already occupied 1S level of the copper atoms and emit electromagnetic radiation. The resulting X-rays are influenced by the unusual electron configuration and are slightly shifted towards lower energies with respect to the characteristic X-rays of copper.

Ramberg and Snow did not detect any violation but were able to put an upper bound on the violation probability of Β²/2 < 1.7 × 10^–26. Following their concept, a much improved version of the experiment, called VIP (violation of the Pauli principle), was set up in the LNGS underground laboratory in Gran Sasso, Italy, in 2006. VIP improved significantly on the Ramberg and Snow experiment by using charge-coupled devices (CCDs) as high-resolution X-ray detectors with a large area and high intrinsic efficiency. In the original VIP setup, CCDs were positioned around a pure-copper cylinder; X-rays emitted from the cylinder were measured without and with current up to 40 A. The cosmic background in the LNGS laboratory is strongly suppressed – by a factor of 10⁶ thanks to the overlying rock – and the apparatus was also surrounded by massive lead shielding.

Setting limits

After four years of data taking, VIP set a new limit on the EP violation for electrons at β²/2 < 4.7 × 10^–29. To further enhance the sensitivity, the experiment was upgraded to VIP2, where silicon drift detectors (SDDs) replace CCDs as X-ray detectors. The VIP2 construction started in 2011 and in 2016 the setup was installed in the underground LNGS laboratory, where, after debugging and testing, data-taking started. The SDDs provide a wider solid angle for X-ray detection and this improvement, together with higher current and active shielding with plastic scintillators to limit background, leads to a much better sensitivity. The timing capability of SDDs also helps to suppress background events.

The experimental programme testing for a possible violation of the EP for electrons made great progress in 2017 and had already improved the upper limit set by VIP in the first two months of running time. With a planned duration of three years and alternating measurement with and without current, a two-orders-of-magnitude improvement is expected with respect to the previous VIP upper bound. In the absence of a signal, this will set the limit on violations of the EP at β²/2 < 10^–31.

Experiments like VIP and VIP2 test the spin-statistics connection for one particular kind of fermions: electrons. The case of EP violations for neutrinos was also theoretically discussed by Dolgov and Smirnov. As for bosons, constraints on possible statistics violations come from high-energy-physics searches for decays of vector (i.e. spin-one) particles into two photons. Such decays are forbidden by the Landau–Yang theorem, whose proof incorporates the assumption that the two photons must be produced in a permutation-symmetric state. A complementary approach is to apply spectroscopic tests, as carried out at LENS in Florence during the 1990s, which probe the permutation properties of ¹⁶O nuclei in polyatomic molecules by searching for transitions between states that are antisymmetric under the exchange of two nuclei. If the nuclei are bosons, as in this case, such transitions, if found, violate the spin-statistics relation. High-sensitivity tests for photons were also performed with spectroscopic methods. As an example, using Bose–Einstein-statistics-forbidden two-photon excitation in barium, the probability for two photons to be in a “wrong” permutation-symmetry state was shown by English and co-workers at Berkeley in 2010 to be less than 4 × 10^–11 – an improvement of more than three orders of magnitude compared to earlier results.

To conclude, we note that the EP has many associated philosophical issues, as Pauli himself was well aware of, and these are being studied within a dedicated project involving VIP collaborators, and supported by the John Templeton Foundation. One such issue is the notion of “identicalness”, which does not seem to have an analogue outside quantum mechanics because there are no two fundamentally identical classical objects.

This ultimate equality of quantum particles leads to all-important consequences governing the structure and dynamics of atoms and molecules, neutron stars, black-body radiation and determining our life in all its intricacy. For instance, molecular oxygen in air is extremely reactive, so why do our lungs not just burn? The reason lies in the pairing of electron spins: ordinary oxygen molecules are paramagnetic with unpaired electrons that have parallel spins, and in respiration this means that electrons have to be transferred one after the other. This sequential character to electron transfers is due to the EP, and moderates the rate of oxygen attachment to haemoglobin. Think of that the next time you breathe!