Aurélien Barrau on why multiple universes should be taken seriously.
Is our entire universe a tiny island within an infinitely vast and infinitely diversified meta-world? This could be either one of the most important revolutions in the history of cosmogonies or merely a misleading statement that reflects our lack of understanding of the most fundamental laws of physics.

Image credit: simulations by Andrei and Dimitri Linde.
A self-reproducing universe. This computer-generated simulation shows exponentially large domains, each with different laws of physics (associated with different colours). Peaks are new “Big Bangs”, with heights corresponding to the energy density.
Image credit: simulations by Andrei and Dimitri Linde. The idea in itself is far from new: from Anaximander to David Lewis, philosophers have exhaustively considered this eventuality. What is especially interesting today is that it emerges, almost naturally, from some of our best – but often most speculative – physical theories. The multiverse is no longer a model; it is a consequence of our models. It offers an obvious understanding of the strangeness of the physical state of our universe. The proposal is attractive and credible, but it requires a profound rethinking of current physics.
At first glance, the multiverse seems to lie outside of science because it cannot be observed. How, following the prescription of Karl Popper, can a theory be falsifiable if we cannot observe its predictions? This way of thinking is not really correct for the multiverse for several reasons. First, predictions can be made in the multiverse: it leads only to statistical results, but this is also true for any physical theory within our universe, owing both to fundamental quantum fluctuations and to measurement uncertainties. Secondly, it has never been necessary to check all of the predictions of a theory to consider it as legitimate science. General relativity, for example, has been extensively tested in the visible world and this allows us to use it within black holes even though it is not possible to go there to check. Finally, the critical rationalism of Popper is not the final word in the philosophy of science. Sociologists, aestheticians and epistemologists have shown that there are other demarcation criteria to consider. History reminds us that the definition of science can only come from within and from the praxis: no active area of intellectual creation can be strictly delimited from outside. If scientists need to change the borders of their own field of research, it would be hard to justify a philosophical prescription preventing them from doing so. It is the same with art: nearly all artistic innovations of the 20th century have transgressed the definition of art as would have been given by a 19th-century aesthetician. Just as with science and scientists, art is internally defined by artists.
For all of these reasons, it is worth considering seriously the possibility that we live in a multiverse. This could allow understanding of the two problems of complexity and naturalness. The fact that the laws and couplings of physics appear to be fine-tuned to such an extent that life can exist and most fundamental quantities assume extremely “improbable” values would appear obvious if our entire universe were just a tiny part of a huge multiverse where different regions exhibit different laws. In this view, we are living in one of the “anthropically favoured” regions. This anthropic selection has strictly teleological and no theological dimension and absolutely no link with any kind of “intelligent design”. It is nothing other than the obvious generalization of the selection effect that already has to be taken into account within our own universe. When dealing with a sample, it is impossible to avoid wondering if it accurately represents the full set, and this question must of course be asked when considering our universe within the multiverse.
The multiverse is not a theory. It appears as a consequence of some theories, and these have other predictions that can be tested within our own universe. There are many different kinds of possible multiverses, depending on the particular theories, some of them even being possibly interwoven.

The most elementary multiverse is simply the infinite space predicted by general relativity – at least for flat and hyperbolic geometries. An infinite number of Hubble volumes should fill this meta-world. In such a situation, everything that is possible (i.e. compatible with the laws of physics as we know them) should occur. This is true because an event with a non-vanishing probability has to happen somewhere if space is infinite. The structure of the laws of physics and the values of fundamental parameters cannot be explained by this multiverse, but many specific circumstances can be understood by anthropic selections. Some places are, for example, less homogenous than our Hubble volume, so we cannot live there because they are less life-friendly than our universe, where the primordial fluctuations are perfectly adapted as the seeds for structure formation.
General relativity also faces the multiverse issue when dealing with black holes. The maximal analytic extension of the Schwarzschild geometry, as exhibited by conformal Penrose–Carter diagrams, shows that another universe could be seen from within a black hole. This interesting feature is well known to disappear when the collapse is considered dynamically. The situation is, however, more interesting for charged or rotating black holes, where an infinite set of universes with attractive and repulsive gravity appear in the conformal diagram. The wormholes that possibly connect these universes are extremely unstable, but this does not alter the fact that this solution reveals other universes (or other parts of our own universe, depending on the topology), whether accessible or not. This multiverse is, however, extremely speculative as it could be just a mathematical ghost. Furthermore, nothing allows us to understand explicitly how it formed.
A much more interesting pluriverse is associated with the interior of black holes when quantum corrections to general relativity are taken into account. Bounces should replace singularities in most quantum gravity approaches, and this leads to an expanding region of space–time inside the black hole that can be considered as a universe. In this model, our own universe would have been created by such a process and should also have a large number of child universes, thanks to its numerous stellar and supermassive black holes. This could lead to a kind of cosmological natural selection in which the laws of physics tend to maximize the number of black holes (just because such universes generate more universes of the same kind). It also allows for several possible observational tests that could refute the theory and does not rely on the use of any anthropic argument. However, it is not clear how the constants of physics could be inherited from the parent universe by the child universe with small random variations and the detailed model associated with this scenario does not yet exist.
One of the richest multiverses is associated with the fascinating meeting of inflationary cosmology and string theory. On the one hand, eternal inflation can be understood by considering a massive scalar field. The field will have quantum fluctuations, which will, in half of the regions, increase its value; in the other half, the fluctuations will decrease the value of the field. In the half where the field jumps up, the extra energy density will cause the universe to expand faster than in the half where the field jumps down. After some time, more than half of the regions will have the higher value of the field simply because they expand faster than the low-field regions. The volume-averaged value of the field will therefore rise and there will always be regions in which the field is high: the inflation becomes eternal. The regions in which the scalar field fluctuates downward will branch off from the eternally inflating tree and exit inflation.
Image credit: simulation by Jean-François Colonna, CMAP/École Polytechnique.
A tri-dimensional representation of a quadri-dimensional Calabi–Yau manifold. This describes the geometry of the extra “internal” dimensions of M-theory and relates to one particular (string-inspired) multiverse scenario.
Image credit: simulation by Jean-François Colonna, CMAP/École Polytechnique. On the other hand, string theory has recently faced a third change of paradigm. After the revolutions of supersymmetry and duality, we now have the “landscape”. This metaphoric word refers to the large number (maybe 10500) of possible false vacua of the theory. The known laws of physics would just correspond to a specific island among many others. The huge number of possibilities arises from different choices of Calabi–Yau manifolds and different values of generalized magnetic fluxes over different homology cycles. Among other enigmas, the incredibly strange value of the cosmological constant (why are the 119 first decimals of the “natural” value exactly compensated by some mysterious phenomena, but not the 120th?) would simply appear as an anthropic selection effect within a multiverse where nearly every possible value is realized somewhere. At this stage, every bubble-universe is associated with one realization of the laws of physics and contains itself an infinite space where all contingent phenomena take place somewhere. Because the bubbles are causally disconnected forever (owing to the fast “space creation” by inflation) it will not be possible to travel and discover new laws of physics.
This multiverse – if true – would force a profound change of our deep understanding of physics. The laws reappear as kinds of phenomena; the ontological primer of our universe would have to be abandoned. At other places in the multiverse, there would be other laws, other constants, other numbers of dimensions; our world would be just a tiny sample. It could be, following Copernicus, Darwin and Freud, the fourth narcissistic injury.
Quantum mechanics was probably among the first branches of physics leading to the idea of a multiverse. In some situations, it inevitably predicts superposition. To avoid the existence of macro-scopic Schrödinger cats simultaneously living and dying, Bohr introduced a reduction postulate. This has two considerable drawbacks: first, it leads to an extremely intricate philosophical interpretation where the correspondence between the mathe-matics underlying the physical theory and the real world is no longer isomorphic (at least not at any time), and, second, it violates unitarity. No known physical phenomenon – not even the evaporation of black holes in its modern descriptions – does this.

Image credit: simulation by Serge Winitzki.
These are good reasons for considering seriously the many-worlds interpretation of Hugh Everett. Every possible outcome to every event is allowed to define or exist in its own history or universe, via quantum decoherence instead of wave function collapse. In other words, there is a world where the cat is dead and another one where it is alive. This is simply a way of trusting strictly the fundamental equations of quantum mechanics. The worlds are not spatially separated, but exist more as kinds of “parallel” universes. This tantalizing interpretation solves some paradoxes of quantum mechanics but remains vague about how to determine when splitting of universes happens. This multiverse is complex and, depending on the very quantum nature of phenomena leading to other kinds of multiverses, it could lead to higher or lower levels of diversity.
More speculative multiverses can also be imagined, associated with a kind of platonic mathematical democracy or with nominalist relativism. In any case, it is important to underline that the multiverse is not a hypothesis invented to answer a specific question. It is simply a consequence of a theory usually built for another purpose. Interestingly, this consequence also solves many complexity and naturalness problems. In most cases, it even seems that the existence of many worlds is closer to Ockham’s razor (the principle of simplicity) than the ad hoc assumptions that would have to be added to models to avoid the existence of other universes.
Given a model, for example the string-inflation paradigm, is it possible to make predictions in the multiverse? In principle, it is, at least in a Bayesian approach. The probability of observing vacuum i (and the associated laws of physics) is simply Pi = Piprior fi where Piprior is determined by the geography of the landscape of string theory and the dynamics of eternal inflation, and the selection factor fi characterizes the chances for an observer to evolve in vacuum i. This distribution gives the probability for a randomly selected observer to be in a given vacuum. Clearly, predictions can only be made probabilistically, but this is already true in standard physics. The fact that we can observe only one sample (our own universe) does not change the method qualitatively and still allows the refuting of models at given confidence levels. The key points here are the well known peculiarities of cosmology, even with only one universe: the observer is embedded within the system described; the initial conditions are critical; the experiment is “locally” irreproducible; the energies involved have not been experimentally probed on Earth; and the arrow of time must be conceptually reversed.
However, this statistical approach to testing the multiverse suffers from severe technical short cuts. First, while it seems natural to identify the prior probability with the fraction of volume occupied by a given vacuum, the result depends sensitively on the choice of a space-like hypersurface on which the distribution is to be evaluated. This is the so-called “measure problem” in the multiverse. Second, it is impossible to give any sensible estimate of fi. This would require an understanding of what life is – and even of what consciousness is – and that simply remains out of reach for the time being. Except in some favourable cases – for example when all the universes of the multiverse present a given characteristic that is incompatible with our universe – it is hard to refute explicitly a model in the multiverse. But difficult in practice does not mean intrinsically impossible. The multiverse remains within the realm of Popperian science. It is not qualitatively different from other proposals associated with usual ways of doing physics. Clearly, new mathematical tools and far more accurate predictions in the landscape (which is basically totally unknown) are needed for falsifiability to be more than an abstract principle in this context. Moreover, falsifiability is just one criterion among many possible ones and it should probably not be over-determined.
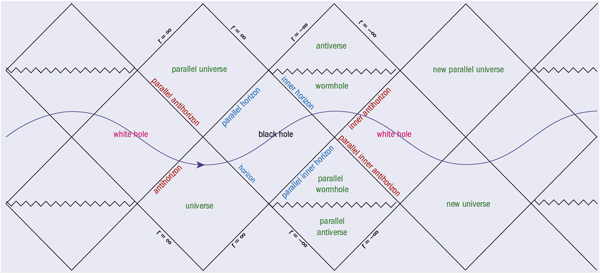
Image credit: from a drawing by Andrew Hamilton.
When facing the question of the incredible fine-tuning required for the fundamental parameters of physics to allow the emergence of complexity, there are few possible ways of thinking. If one does not want to use God or rely on an unbelievable luck that led to extremely specific initial conditions, there are mainly two remaining possible hypotheses. The first would be to consider that since complexity – and in particular, life – is an adaptive process, it would have emerged in nearly any kind of universe. This is a tantalizing answer, but our own universe shows that life requires extremely specific conditions to exist. It is hard to imagine life in a universe without chemistry, maybe without bound states or with other numbers of dimensions. The second idea is to accept the existence of many universes with different laws where we naturally find ourselves in one of those compatible with complexity. The multiverse was not imagined to answer this specific question but appears “spontaneously” in serious physical theories, so it can be considered as the simplest explanation to the puzzling issue of naturalness. This of course does not prove the model to be correct, but it should be emphasized that there is absolutely no “pre-Copernican” anthropocentrism in this thought process.
It could well be that the whole idea of multiple universes is misleading. It could well be that the discovery of the most fundamental laws of physics will make those parallel worlds totally obsolete in a few years. It could well be that with the multiverse, science is just entering a “no through road”. Prudence is mandatory when physics tells us about invisible spaces. But it could also very well be that we are facing a deep change of paradigm that revolutionizes our understanding of nature and opens new fields of possible scientific thought. Because they lie on the border of science, these models are dangerous, but they offer the extraordinary possibility of constructive interference with other kinds of human knowledge. The multiverse is a risky thought – but, then again, let’s not forget that discovering new worlds has always been risky.





