Over the past decade the technique of frequency map analysis, developed to study astronomical systems, has shown its value in an increasing number of areas, including the analysis of particle orbits in accelerators.

At first glance, any close association between the planets of the solar system – huge masses of rock, liquid and gas gently guided by gravity through the vast emptiness of space – and the mad traffic of tightly bunched particles in a circular accelerator, crushed together by fierce radiofrequency and magnetic fields, could hardly seem less likely.
Nonetheless, the dynamics of planets moving through our solar system and particles moving in accelerators do share many similar features. Both demand an analysis of the evolution of a dynamic system over a very long time – up to 1 billion revolutions for both the solar system and the Large Hadron Collider (LHC) at CERN. In addition, these systems can be studied to a first approximation as though they were non-dissipative (although radiation damping is not negligible when synchrotron radiation becomes significant, as in electron storage rings).
Over the last 10 years the relatively new technique of frequency map analysis has turned out to be very effective when applied to the analysis of numerical simulations in physical systems – particularly those with three or more degrees of freedom – which may be as large as the solar system or even an entire galaxy, or as small as the particles in an accelerator.
The frequency mapping technique was recently applied for the first time to measured rather than simulated electron trajectories in a storage ring, at the Advanced Light Source (ALS) at the Lawrence Berkeley National Laboratory. The aim was to reveal the dynamics of an actual particle beam.
Chaotic motion
The story of frequency map analysis began in 1989 when Jacques Laskar (Bureau des Longitudes, Paris) demonstrated that the motion of the solar system is chaotic (Laskar 1989). He showed that the separation between two orbits with similar initial conditions will diverge exponentially over time (e.g. the distance between the orbits will increase by a factor of 10 every 10 million years).
In practice, this means that, although it is possible to make a useful prediction for the evolution of the solar system over 10 million years, it is essentially impossible to ascertain what the planetary positions will be after 100 million years have passed.
So will the Earth collide with Venus or Mars within the next few billion years? Thankfully, this possibility seems to have been ruled out (Laskar 1990), but it is difficult to understand more precisely the behaviour of this chaotic system with a large number of degrees of freedom. For this reason, Laskar began developing the frequency map analysis technique.
Frequency map analysis involves looking at the dynamics in frequency rather than configuration space. Any regular and quasi-periodic motion appears as a fixed point in frequency space, where it will be characterized by the values of its fundamental frequencies (one per degree of freedom).
By contrast, irregular trajectories will be subject to some diffusion in frequency space (the frequencies will change with time). The map from initial conditions to points in frequency space is regular in regions where the trajectories are regular, and irregular where the trajectories are chaotic.
The full dynamics of the system can thus be analysed by varying the initial conditions (in position or momentum) of the system and computing the fundamental frequencies for each set of initial conditions. To accomplish this, a numerical integration of the equations of motion and a fast-converging modified Fourier technique can be used to obtain a quasi-periodic approximation of the calculated trajectories.
Adapting to the accelerator
Frequency map analysis was applied to particle accelerators for the first time in 1992, when Scott Dumas, a mathematician from Cincinatti, visited the Bureau des Longitudes to discuss some of the difficulties that arise in accelerator dynamics. Laskar realized that his new technique could very well be adapted to accelerators, and the following year Laskar and Dumas published a letter in Physical Review Letters applying the technique to a simple accelerator model that had previously been studied extensively by other means (Dumas and Laskar 1993).
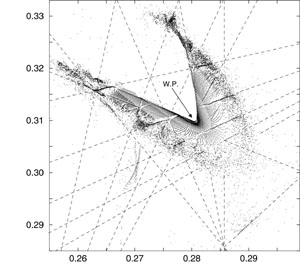
In a circular accelerator, focusing magnetic fields cause particles to oscillate transversely about the closed, central trajectory. The number of oscillations in one turn around the ring is called the betatron tune and can be different in the horizontal and vertical directions. Additionally, the oscillations are nonlinear and the oscillation frequencies change with the transverse amplitude of the particles.
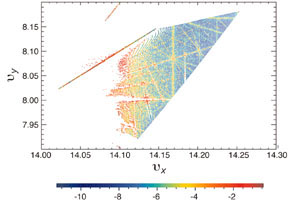
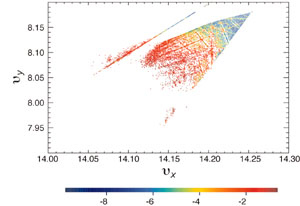
In this context the fundamental frequencies extracted from the frequency map analysis correspond to the tunes for each trajectory. The amplitude of the transverse particle motion is mapped into frequency space by associating a pair of fundamental frequencies with the horizontal and vertical transverse amplitudes. This frequency map is displayed in a coordinate system with the horizontal and vertical tunes as the axes.
From the nominal working point corresponding to small transverse amplitude oscillations, the frequencies shift over a wide area as the amplitudes of the betatron oscillations increase. The motion of electrons with large transverse amplitudes may be influenced by resonances. Damaging resonances show as distortions in the map.
This publication led Laskar to a 1994 conference on Nonlinear Dynamics in Particle Accelerators held in the Tuscan town of Arcidosso, where he presented a model of Berkeley’s ALS, a 1.9 GeV electron storage ring designed to generate synchrotron radiation with the highest brightness in the soft X-ray region.
David Robin, now ALS Accelerator Physics Group leader, was in the audience and immediately invited Laskar to a working-group meeting later in the conference. This resulted in an ongoing collaboration between the Astronomie et Systèmes Dynamiques group at the Bureau des Longitudes and ALS accelerator physicists, with the goal of investigating this new application of frequency map analysis to the study of ALS dynamics.
At first the collaborators applied frequency map analysis to numerically generated data from a model. In these simulations the frequency maps turned out to be very sensitive to the distribution of magnetic-field errors in the model.
Even for a machine with very small field errors, there was a striking difference in the frequency map compared with the frequency map of an ideal machine. Smaller stable areas and larger chaotic regions resulting from the errors emphasized the importance of accurate machine models.
During this period, accelerator physicists were also applying the frequency map analysis technique to several other synchrotron radiation storage rings, including those at the Stanford Synchrotron Radiation Laboratory (Stanford Linear Accelerator Center), the European Synchrotron Radiation Facility (Grenoble) and the Laboratoire pour l’Utilisation du Rayonnement Electromagnétique (Orsay), as well as the recently approved French synchrotron source, SOLEIL.
In the high-energy physics field, the frequency map analysis technique is finding a role in the evolution of the design of the LHC (Papaphilippou 1999). To take one example, when making changes in the magnet lattice, accelerator physicists want to know with considerable confidence that it will be possible to accumulate particles in the storage ring during the rather lengthy injection process (10 million turns round the ring). Frequency map analysis provides a global view of the resonance structure and other features of the phase space, thereby enabling accelerator physicists to avoid areas which might be dangerous.
Constructing experimental frequency maps based on measured beam oscillations and using them to optimize performance takes frequency map analysis beyond simulations to operating accelerators. A step in this direction has now been taken at the ALS (Robinet al.2000), using two tools to provide the required data.







