Neutrinos could point to a deeper theory of elementary particles.

Image credit: T2K Collaboration.
The 1998 discovery that neutrinos can oscillate between different flavours, by the Super-Kamiokande experiment in Japan and subsequently by the SNO experiment in Canada, marked a turning point in our understanding of elementary particles. For many theorists, it represents the first hard particle-physics evidence for the existence of new degrees of freedom (d.o.f.) beyond the known fundamental particles and, most probably, of new physics beyond the Standard Model (SM). The hunt to uncover the new theory is the main focus of the neutrino theoretical community.
First postulated by Pauli in 1930, neutrinos have always played the role of the elusive particle. Their interactions were soon understood thanks to Fermi’s beta-decay theory, but searching for them seemed more like science fiction, at the time. In 1946, however, Pontecorvo suggested that nuclear reactors and the Sun are copious sources of neutrinos, and proposed a radiochemical method for the detection of neutrinos.
A decade later, Reines and Cowan established the neutrino’s existence by performing a reactor neutrino experiment, and the search for astrophysical neutrinos began soon afterwards. Ray Davis Jr and collaborators later detected solar neutrinos, reporting in 1972 a flux that was significantly smaller than predicted by the most sophisticated solar models developed by John Bahcall. This “solar-neutrino puzzle” was eventually explained in terms of the proposal by Bruno Pontecorvo in 1957 and 1958, applied by him to solar neutrinos in 1967, that neutrinos may oscillate between their different types. Combined with the 1962 proposal by Maki, Nakagawa and Sakata – inspired by the discovery of the muon neutrino in the well-known Brookhaven experiment – that there exists mixing between flavour and massive neutrino states, the stage was set to catch and “see” an oscillating neutrino.
Proving this elegant theoretical picture took a further 36 years of experimental innovation. In the end, it relied on the observation of atmospheric neutrinos produced by collisions of cosmic rays in the upper atmosphere, which produce showers of pions and kaons whose subsequent decays give muon and electron neutrinos. Atmospheric neutrinos were first detected in 1965 by the Kolar Gold Fields experiment in India and another experiment at the East Rand gold mine in South Africa. Then, in 1998, in a momentous discovery, Super-Kamiokande showed that muon neutrinos disappear as a function of distance travelled (see figure 1). Just a few years later, thanks to measurements of the total solar-neutrino flux, the SNO experiment confirmed that solar neutrinos can transform from electron neutrinos into muon and tau neutrinos. These two milestones and subsequent results, which have been recognised by a number of prestigious awards, ushered in a mesmerising period of new results that continues to this day.
Neutrino oscillations are the transformation of a neutrino from one flavour into another as it propagates. It is a fundamentally quantum-mechanical process arising from a misalignment of flavour states, νe, νμ and ντ, which describe neutrinos in production and detection, compared with the mass eigenstates, ν1, ν2 and ν3. At the source, a flavour neutrino is the coherent superposition of mass states, which propagate with different phases due to their different masses. As neutrinos travel, the shift in phase results in a different combination of flavour neutrinos. The existence of neutrino oscillations necessarily requires neutrinos to have masses and to mix, which is different from the prediction of the SM (at least in its minimal form). This is why it is widely believed that neutrino oscillations are the first and so far only concrete evidence for physics beyond the SM provided by particle-physics experiments.
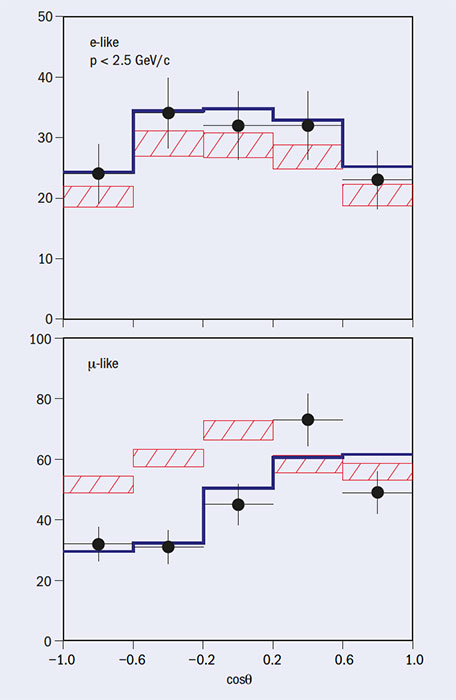
Image credit: Phys. Rev. Lett. 81 1562.
The decade following the discovery of neutrino oscillations did not disappoint. In 2002, the KamLAND experiment in Japan reported the first oscillations of man-made neutrinos, produced by nuclear reactors, while the K2K and MINOS experiments detected neutrinos from accelerator-produced beams. Together with the ongoing T2K and NOvA experiments, as well as atmospheric-neutrino observations at Super-Kamiokande, these experiments have established that there are two mass-squared differences that drive different neutrino oscillations and imply the existence of at least three neutrino mass eigenstates. The data also show that neutrino mixing is described by a 3 × 3 unitary matrix parameterised by three well-measured angles: θ12, θ23 and θ13.
We have now an incredibly rich picture of neutrino properties that was unthinkable at the time of the Super-Kamiokande results and that is very different from that of the quarks. But despite these immense achievements, we are still in need of crucial pieces of information to reach a complete understanding of neutrino properties.
The most important question about neutrinos concerns the type of masses they have. So far, all the known fermions are of the Dirac type: their particles and antiparticles have opposite charges and they possess a Dirac mass that arises from the coupling to the Higgs field. Neutrinos could behave in the same way, but because they are electrically neutral it is possible that neutrinos acquire mass via a different mechanism. Indeed, neutrinos and antineutrinos might be indistinguishable, constituting what is called a Majorana particle after Ettore Majorana who proposed the concept in 1937. Unlike Dirac fields, which have four components, Majorana fields have only two d.o.f. Such a particle cannot possess any charge, not even a lepton number.
A matter of conservation
The question of the nature of neutrinos is therefore intrinsically related to the conservation of the lepton number. In the SM, the lepton number is a global accidental symmetry that happens to be preserved thanks to the gauge symmetries and particle content, but it does not have a dynamic role because there are no associated gauge bosons. The question arises whether the ultimate theory of particles and their interactions is lepton-number violating or not. The most promising way to answer this question is to search for neutrinoless double-beta decay, whereby certain nuclei spontaneously undergo two beta decays at once, without producing any neutrinos. This process directly violates lepton-number conservation and would imply that neutrinos are Majorana particles, motivating a broad international experimental programme (see panel below).
A second major question is whether the CP symmetry is violated in the lepton sector, as it is in the quark one. CP violation is one of the three key ingredients in baryogenesis and leptogenesis, which are needed to dynamically explain the observed matter–antimatter asymmetry of the universe (see panel below). There are three possible sources of CP violation in the lepton sector: the Dirac phase, which is the analogue of the one in the quark sector, and two Majorana phases that appear only if neutrinos are Majorana particles. If neutrinos are Dirac particles, the latter can be rotated away as is done in the quark sector.
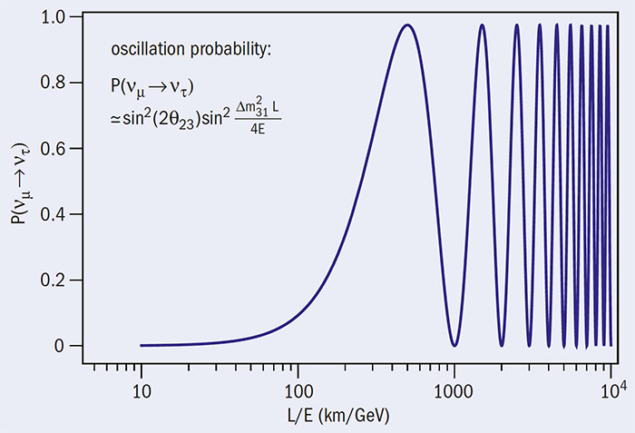
The first hints of leptonic CP violation came recently from combining data from China’s Daya Bay experiment with measurements at long-baseline accelerator facilities, in particular T2K and NOvA. These seem to indicate a preference for a nonzero value of the CP-violating Dirac phase (see figure 2). It is too early to tell, but very ambitious plans – including the proposed Deep Underground Neutrino Experiment (DUNE) in the US and T2HK in Japan – aim to settle the issue by allowing both neutrino and antineutrino oscillations to be studied. The latter behave differently if Dirac CP violation is present, with oscillations that are being enhanced or suppressed, depending on the values of the Dirac phase.
The other mixing parameters, namely the three mixing angles, are already quite well-determined. Angle θ13 went from being unknown just over four years ago to being the best-measured, thanks to results from the Daya Bay as well as RENO and Double Chooz experiments, while the JUNO experiment in China plans to reach a sub-per-cent accuracy for the θ12 angle after a few years of operation. θ23 is particularly interesting because it could be exactly maximal, therefore pointing towards a symmetry in the lepton-flavour sector, or could deviate from this by several degrees. Current and future long-baseline oscillation experiments will have the best chance of determining θ23, which will be critical for disentangling the different models proposed to explain the observed mixing pattern.
Massive considerations
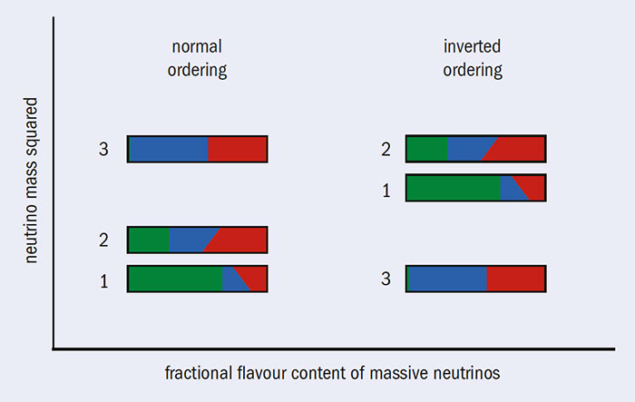
As for the values of the neutrino masses themselves, we already have a very precise measurement of the absolute values of the two mass-squared differences – which differ by a factor of about 30 (figure 2). But we still lack key pieces of information, namely which neutrino is the lightest, defining the neutrino mass ordering, and what its mass scale is. The sign of the solar mass-squared difference is determined by solar-neutrino oscillations, but that of the atmospheric one is unknown. If it turns out to be positive, corresponding to m3 > m1, neutrino masses exhibit the so-called “normal” ordering. The alternative scenario, m3 < m1, implies an “inverted” ordering (figure 3).
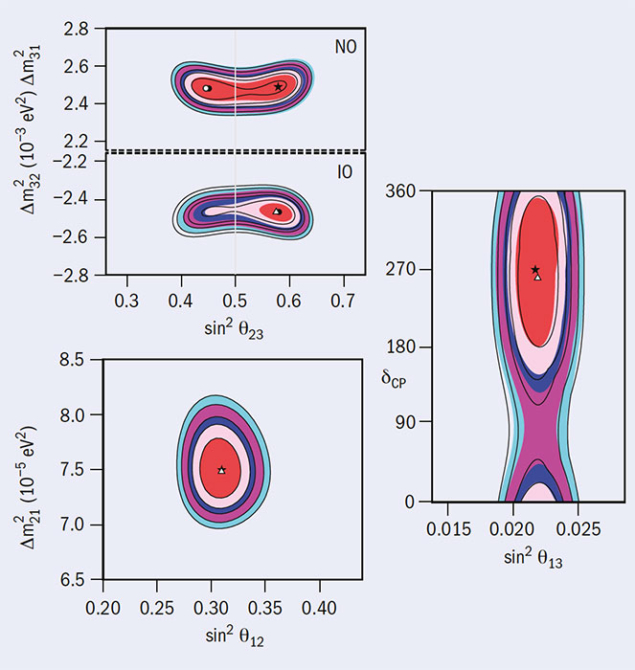
Knowing the mass ordering and scale is important for theorists because different theoretical models predict different patterns, and also for experimentalists searching for specific signatures. It strongly affects the rate of neutrinoless double-beta decay, substantially impacting on the prospects of discovering the Majorana nature of neutrinos, while in the early universe heavier neutrinos suppress the growth of large-scale structures at small scales. The ordering of the masses also changes the way in which neutrinos propagate over long distances in media such as the Earth, due to weak interactions with the background of electrons, protons and neutrons. This gives neutrinos an effective mass that modifies their energies and the mixing: neutrino oscillations are enhanced for normal mass ordering and suppressed for inverted ordering, with the opposite happening in the case of antineutrinos.
Experiments such as the long-baseline experiment NOvA, which measures a neutrino beam produced 810 km away at Fermilab, exploit these effects to hunt for the neutrino mass ordering (see “NOvA releases new bounds on neutrino mixing parameters”). With DUNE, which will operate at a distance of 1300 km, and new atmospheric-neutrino observatories such as PINGU, ORCA and INO, as well as JUNO, we expect to resolve this issue in the next 5–10 years.
However, even knowing the neutrino mass ordering still leaves open the question of the overall neutrino mass scale. So far, we know that neutrino masses cannot be too large. They are restricted to be smaller than 2.2 eV by the Troitsk and Mainz experiments, and well below this limit if one considers cosmological observations, which suggest a conservative bound on the sum of the masses of around 0.7 eV in the standard cosmological model. The KArlsruhe TRItium Neutrino (KATRIN) experiment currently being commissioned in Germany aims to determine the absolute mass scale by searching for a small deformation of the electron energy spectrum in beta decays and will be sensitive to neutrino masses as small as 0.2 eV. It is expected to take data very soon.
The standard neutrino picture comprises three neutrino flavour states and correspondingly three light-mass eigenstates. In many extensions of the SM this is not the case because new degrees of freedom and/or new interactions can be added (see panel below). The simplest extension is that of sterile-neutrinos, which do not experience SM interactions. The corresponding nearly sterile neutrino mass could take any value, from the very small to the GUT scale, but in many phenomenological studies is around the eV scale and therefore could induce short-baseline oscillations.
Results from the LSND and MiniBooNE experiments in the US, as well as some reactor neutrino ones, have hinted at precisely such a signal. But the results are still controversial, and there is tension with other searches of sterile-neutrinos from short-baseline muon neutrino experiments. New short-baseline reactor and radioactive-source neutrino experiments, in addition to the dedicated short-baseline accelerator programme at Fermilab involving the MicroBooNE, ICARUS and SBND detectors, will shed light on these results and possibly hunt for nearly sterile-neutrinos with even smaller mixing angles. A positive signal would be groundbreaking, forcing us to rethink the theoretical framework for light neutrinos and posing new questions about the nature, masses, mixing and CP-violating properties of the new states.
Indeed, neutrinos remain the most intriguing and elusive of all known fermions and are an ideal portal to explore new physics beyond the Standard Model. Despite impressive progress in the past 20 years, going from not knowing if neutrino oscillations took place to having measured most of the oscillation parameters with great precision, many key phenomenological and theoretical questions remain open and urgently require answers. Fortunately, a broad and exciting experimental programme is under way and, as is often the case in research, the focus of our theoretical work could change in an instant. With the LHC now into its high-energy run, for example, it is possible that we will discover entirely new particles and phenomena beyond the SM. We would then need to establish what connection – if any – exists between this and the already new physics of neutrino masses. Or perhaps neutrino masses come from a secluded sector, possibly at energy scales so high that we cannot test it directly. These and many other questions, informed by the current wealth of new and upcoming experiments, promise to keep neutrino theorists occupied for the foreseeable future.
Searching for the neutrino’s fundamental nature
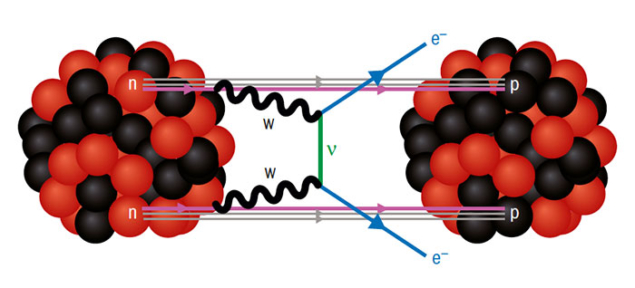 Two-neutrino double beta decay (DBD) is a very rare Standard Model process that causes two neutrons simultaneously to decay into two protons and two electrons, with the emission of two electron antineutrinos. If neutrinos are Majorana particles, however, instead of being emitted, the Majorana neutrinos can mediate a new process called neutrinoless double-beta decay (NDBD), which is not allowed in the Standard Model. Observing this process would be groundbreaking because it would imply that the lepton number is violated and provide crucial information about neutrino masses. More than a dozen experiments worldwide are searching for NDBD which, like DBD, can be observed in nuclei in which ordinary beta decay is kinematically forbidden. Because NDBD produces no neutrinos to carry off energy, all events will be concentrated at the end point of the two-electron energy spectrum – unlike the case for DBD, in which the spectrum is a continuum. Being an extremely rare process, NDBD searches require sufficiently large detector volumes, very good energy resolution, a location deep underground and extremely low backgrounds. 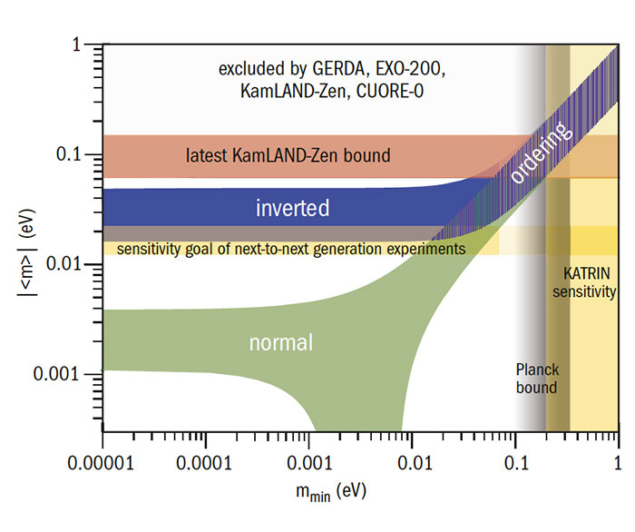 A number of different experimental techniques are being employed. Liquid-scintillator detectors such as KamLAND-Zen in Japan and SNO+ in Canada offer large target masses, and currently KamLAND-Zen provides the strongest bound on NDBD with a half-life greater than 1.1 × 1026 years. Germanium detectors such as GERDA and MAJORANA are more compact and ensure very good energy resolution, while planned experiments such as SuperNEMO and DCBA can track both electrons and could reconstruct their angular distribution. Time projection chambers, such as nEXO in the US and NEXT in Spain, can simultaneously track the electrons and allow large target volumes, while bolometers such as CUORE and AMoRE benefit from very high energy resolution. Despite this impressive armoury, NDBD hunters are at the mercy of the neutrino masses and mixing parameters (see main text). The NDBD rate depends crucially on the combination of masses and mixing parameters, the so-called effective Majorana mass parameter. If neutrinos exhibit an inverted mass ordering, the predicted lower bound on the decay rate will be just within reach of the next-to-next generation of experiments. If they adopt the normal mass ordering, the decay rate could be anywhere between the current bounds and zero, if a specific cancellation between the three massive neutrinos is at work (see figure).
|
Messengers from beyond the Standard Model
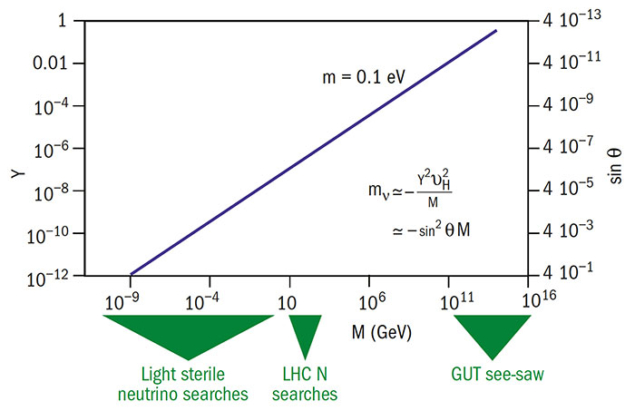 The origin of neutrino masses and mixing is still unresolved, and necessarily requires new degrees of freedom and new interactions. The simplest extension of the Standard Model assumes the existence of right-handed (RH) neutrinos, which behave as singlets with respect to the Standard Model gauge group. Unless specific symmetries are imposed, Yukawa couplings with the lepton doublet and the Higgs will be allowed and the lepton number will be preserved. Dirac masses therefore arise for neutrinos as they do for all the other known fermions, but this mechanism provides no insight as to why neutrino masses are so small (the Yukawa coupling needed would be 12 orders of magnitude smaller than that of the top quark). One could simply accept such extreme fine-tuning as a fact of nature, but this would naively lead one to expect the same mixing in the lepton sector as in the quark one and a similar mass ordering, neither of which is observed. The alternative option is that neutrinos are Majorana particles. Majorana neutrinos will have a mass term in the Lagrangian that breaks lepton-number conservation. Although this mass term is forbidden by the gauge group of the SM, it could arise as the low-energy realisation of a higher-energy theory. This can explain both the existence of neutrino masses and their smallness, because a strong suppression is induced by the new heavy scale. Theorists are working hard to understand what the new theory at high energy might be. The ultimate theory behind neutrino masses must also explain the observed mixing structure, the presence of CP violation (if observed), and why the lepton sector contains large angles that are different to the quark sector. Many approaches have been proposed, for instance the use of continuous or discrete flavour symmetries, but no unique underlying principle has yet been identified. The simplest and most studied extension beyond the SM for neutrino masses is the “see-saw type I” mechanism. Because RH neutrinos are completely neutral with respect to the SM gauge symmetries, they could be much heavier than the other known fermions. The Lagrangian would then contain both a Yukawa coupling with the Higgs, as for the quarks, and a Majorana mass term, M, for the RH neutrinos. Once the neutral Higgs boson gets a vacuum expectation value, light masses for the neutrinos arise that are proportional to the square of the Yukawa couplings and suppressed by M. Taking an order-one Yukawa coupling and M of around 1014 GeV, we obtain a sub-eV neutrino mass scale as required by the data and, because the lepton number is violated by M, the light neutrinos will be Majorana particles. This is by no means the only way to give origin to neutrino masses. First of all, since the RH neutrino masses can take any value, the scale of the see-saw mechanism could be lowered even below the electroweak scale, allowing some models to be tested at the LHC. Typical signatures are same-sign dileptons with no missing energy, indicating lepton-number violation, and flavour-violating multi-lepton events. Several searches have been conducted by the LHC’s ATLAS and CMS collaborations, but so far no positive hint has been found. The heavy particles responsible for the see-saw mechanism could also be different: a fermion triplet in see-saw type III and a scalar triplet in see-saw type II models. Some models, such as radiative and R-parity-violating supersymmetric models, do not invoke the see-saw mechanism at all. With so many possibilities, clearly one needs to hunt for other beyond-SM signatures to try to identify the origin of neutrino masses. Leptogenesis is a key one. To generate dynamically a baryon asymmetry in the early universe, the three Sakharov conditions need to be satisfied: lepton or baryon number violation, C and CP violation, and an out-of-equilibrium state (satisfied by the expansion of the universe). The see-saw mechanism can satisfy all of these conditions. In the early universe, RH neutrinos got out of equilibrium once the temperature dropped below their mass. Thanks to their decays into leptons and Higgs bosons, a net lepton asymmetry could arise if the rate in one channel and the conjugated one are different due to CP violation. This asymmetry would then be converted into a baryon asymmetry by non-perturbative SM effects. Observing CP violation in future neutrino-oscillation experiments and lepton-number violation in neutrinoless double-beta-decay searches would therefore provide strong hints that leptogenesis is at the origin of the baryon asymmetry of the universe.
|






3 Comments