The “hidden” dimensions of string theory may be much larger than was previously thought and may soon come within experimental reach, together with the strings themselves. Ignatios Antoniadis gives an introduction to string physics and describes how it may soon be testable at particle colliders.

Look in front of you. Now to your side. Next, up above. These are the known spatial dimensions of the universe: there are just three. Have you ever wondered about the origin of this number? Have you ever thought there might be new dimensions that escape our observation? In all physical theories, the number of dimensions is a free parameter that is fixed to three by observation – with one exception. This exception is string theory, which predicts the existence of six new spatial dimensions. At present, it is the only known theory that unifies the two great discoveries of the 20th century: quantum mechanics, which describes the behaviour of elementary particles, and Einstein’s general relativity, which describes gravitational phenomena in our universe (M B Green et al. 1987).
String theory replaces all the elementary point particles that form matter and mediate interactions with a single extended object of vanishing width: a tiny “string”. Thus, every known elementary particle, such as the electron, quark, photon or neutrino, corresponds to a particular vibration mode of the string, as shown in figure 1. The diversity of these particles is due to the different properties of the corresponding string vibrations. Until now there has been no experimental confirmation of string theory, and no-one has ever observed strings, not even indirectly, or the space of extra dimensions where they live. The main arguments in favour of the idea are theoretical, because this provides a coherent framework for the unification of all fundamental interactions.
For a long time string physicists thought that strings were extremely thin, having the smallest possible size in physics, associated with the Planck length, of 10-35 m. Recently, however, the situation has changed dramatically. It seems that the “hidden” dimensions of string theory may be much larger than we previously thought, and they may come within experimental reach in the near future, together with the strings themselves (I Antoniadis 1990, J D Lykken 1996, N Arkani-Hamed et al. 1998, I Antoniadis et al. 1998). These ideas are leading towards the experimental testing of string theory, which can be performed at Fermilab’s Tevatron and the future Large Hadron Collider (LHC) at CERN.
The main motivation for these ideas came from the considerations of the so-called mass hierarchy problem: why does the gravitational force remain much weaker than the other fundamental forces (electromagnetic, strong and weak), at least up to the energies currently reached in high-energy physics? In quantum theory the masses of elementary particles receive important quantum corrections that are of the order of the higher energy scale present in the theory. So in the presence of gravity the Planck mass (1019 GeV) pulls all the familiar particles of the Standard Model to be 1016 times heavier than we observe. To avoid this catastrophe the parameters of the theory must be adjusted by up to 32 decimal places, resulting in a very ugly “fine tuning”.
A possible solution is provided by the introduction of a new fundamental symmetry of matter, called supersymmetry, at energies where electromagnetic and weak effects unite into electroweak interactions. One of the main predictions of supersymmetry is that every known elementary particle has a partner, called a superparticle. However, as none of these superparticles has ever been produced at an accelerator, they must be heavier than the observed particles. Supersymmetry must therefore be broken. On the other hand, protection of the mass hierarchy requires that its breaking scale – that is, the mass splitting between the masses of ordinary particles and their partners – cannot be larger than a few TeV. Such particles could therefore be produced at the LHC, which will test the idea of supersymmetry.
Alternatively, an idea proposed in the past few years solves the problem if the fundamental string length is fixed to 10-18 to 10-19 m (I Antoniadis et al. 1998). In this case, the quantum corrections are controlled by the string scale, which is in the TeV region, so they do not destabilize the masses of elementary particles. Moreover, the new idea offers the remarkable possibility that string physics may soon be testable at particle colliders.
The universe as a braneworld
How is it possible to lower the string scale from the Planck scale of traditional quantum gravity to the TeV region without contradicting observations? In particular, why does gravity interact much more weakly with our world, what happens to the extra dimensions of string theory and why have they not been observed?

String theory has a long history. It was introduced about 40 years ago in order to describe strong interactions, and it took a decade to understand that it was a natural candidate for quantum gravity. Ten years later, it was realized that it can unify all fundamental forces, while in the past decade there has been a real breakthrough in understanding several aspects of its non-perturbative dynamics.
This breakthrough was not realized earlier because prior to 1994 most of the research was done in the context of the so-called Heterotic string theory, which initially looked more promising for physics and more attractive theoretically. In this theory, the string scale is fixed by the Planck mass and cannot be lowered. However, there were five consistent string theories in total, which created a problem as string theory was supposed to provide a unified framework of all physical theories. We now believe that every known string theory describes a particular limit of an underlying more general fundamental theory that can be defined in 11 dimensions of space, called M-theory, as illustrated in figure 2 (E Witten 1995).
A crucial role in these developments was played by the discovery of “p-branes”, which are higher dimensional objects extended in p spatial dimensions, so generalizing the notion of a point particle (p = 0) or a string (p = 1). One of the main consequences of this discovery is that the string scale is, in general, a free parameter that can be dissociated from the Planck mass if the universe is localized on a p-brane and does not feel all the extra dimensions of string theory. The braneworld description of our universe separates the dimensions of space into two groups: those that extend along our p-braneworld, called parallel dimensions, and those transverse to it. Obviously the parallel ones must contain at least the three known dimensions of space, but they may contain more. If our universe has additional dimensions, we should observe new phenomena related to their existence. So why has nobody detected them until now?
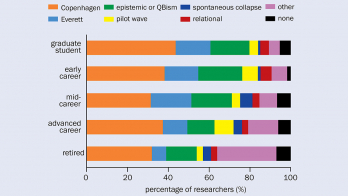
A possible answer was given at the beginning of the 20th century by Theodore Kaluza and Oskar Klein (T Kaluza 1921, O Klein 1926), who said that we cannot detect the new dimensions because their size is very small, in contrast to the infinitely large size of the other three that we know. An infinite and narrow cylinder, for example, is a two-dimensional space, with one dimension forming a very small circle. While you can move infinitely far away along the axis, you return back to the same point when moving along the orthogonal direction (see figure 3).
If one of the three known dimensions of space was small, say of millimetre size, we would be flat, and while we could move freely towards left or right, forward or backward, it would be impossible to go more than a few millimetres up or down where space would end. So extra dimensions along our universe escape observation if their size is less than 10-18 m, as they require energies higher than those we currently have at our disposal (I Antoniadis and K Benakli 1994, I Antoniadis et al. 1994, 1999).
The next question is how could we detect the existence of these extra dimensions if we did have sufficient energy to probe their size? (The minimum energy required is given by their inverse size and is called the “compactification scale”.) The answer was again given by Kaluza and Klein, who stated that the motion of a particle in extra dimensions of finite size manifests itself to us as a tower of massive particles, called “Kaluza-Klein excitations”. If for instance the photon propagates along an extra-compact dimension, we would observe a tower of massive particles with the same properties as the photon but with a mass that becomes larger as the size of the extra dimension decreases. It follows that for a size of the order of 10-18 m, an energy of the order of a few TeV would be sufficient to produce them.
The above analysis and bound on sizes does not apply, however, for dimensions transverse to our universe, as we cannot send light or any form of observable matter to probe their existence. The only way to communicate in this case is through gravity, which couples to any kind of energy density. However, our knowledge of gravity at short distances is much less than for the other interactions, allowing the sizes of such “hidden” dimensions to be as large as a millimetre, which is roughly the shortest distance at which Newton’s law is tested in the laboratory.
The string scale at TeV energies

An attractive and calculable braneworld framework that allows the dissociation of the string and Planck scales without contradicting observations is provided by the so-called type I string theory. In this theory, gravity is described by closed strings, which propagate in all nine dimensions of space, while matter and all other Standard Model interactions are described by open strings that end on a particular type of p-brane, called a D-brane (where D stands for Dirichlet), as shown in figure 4 (J Polchinski 1995).
In the framework of type I string theory, the string scale can be lowered in the TeV region at the expense of introducing large transverse dimensions that are much bigger than the string length. Actually, the string scale fixes the energy at which gravity becomes coupled with a strength comparable to the other three interactions, thus realizing the unification of all fundamental forces at energies lower, by a factor 1016, than we have previously thought. However, gravity appears very weak at macroscopic distances because its intensity is spread in the large extra dimensions known as the “bulk” (N Arkani-Hamed et al. 1998).
The basic relation between the fundamental (string) scale and the observed gravitational strength is: total force = observed force x transverse volume, thus expressing Gauss’s law for higher dimensional gravity. In order to increase the gravitational force to the desired magnitude without contradicting current observations, one has to introduce at least two extra dimensions of a size that can be as large as a fraction of a millimetre. In the case of one transverse dimension, the required size is of astronomical distances, which is obviously excluded, while for more than two dimensions it should be smaller, down to the fermi scale (10-14 m) in the case of six dimensions. At distances smaller than the size of the extra dimensions, gravity should start to deviate from Newton’s law, which it may be possible to explore in laboratory table-top experiments (see figure 5).
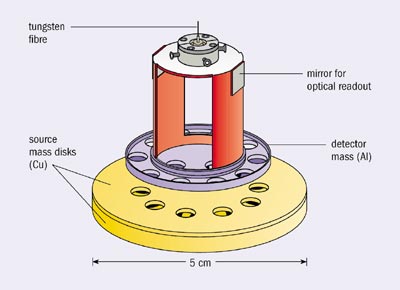
Type I string theory provides a realization of this idea in a coherent theoretical framework, where the string scale is fixed in the TeV region as required for the stability of the mass hierarchy, corresponding to a size of around 10-18 m. For the theory to be calculable, parallel dimensions should not be much bigger than the string length, while the size of transverse dimensions is fixed by the observed value of Newton’s constant. This size should therefore vary from the fermi scale to a fraction of a millimetre, depending on the number of dimensions (varying from six to two, respectively). It is remarkable that this possibility is not only consistent with present observations, but also presents a viable and theoretically well motivated alternative to low-energy supersymmetry. It simultaneously offers a plethora of spectacular new phenomena, which can be tested in laboratory experiments and may provide surprises at the LHC and other particle accelerators.
String theory under experimental test
There are several tests of these new ideas, either in laboratory experiments that look for deviations of Newton’s law at submillimetre distances, or at particle colliders. In microgravity experiments it is only possible to explore the case of two extra dimensions, because only in this case are deviations expected to appear at distances close to present limits. In fact the inverse square law of gravitational attraction, 1/r2, between two masses at a distance r should change to 1/r2+n if there are n large extra dimensions. However, at distances of the order of the size of the extra dimensions, only the first Kaluza-Klein excitations of the graviton are probed, generating an extra Yukawa force of strength comparable to ordinary gravity and of a range equal to the size of the dimensions. The present experimental bounds on such forces are displayed in figure 6 as a function of their range λ (horizontal axis) and their strength relative to gravity α (vertical axis) (C D Hoyle et al. 2001, J C Long et al. 2002).
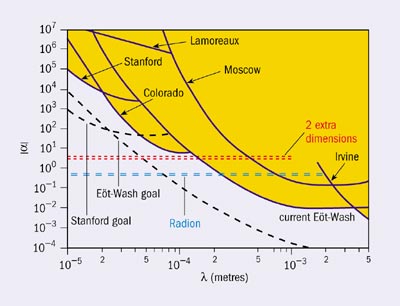
Besides the violation of Newton’s law due to the presence of extra dimensions, there may be additional sources of new forces in a large class of models with supersymmetric bulk. In these models, motivated mainly from vacuum stability and model building, supersymmetry is not realized in our world because our brane universe is not supersymmetric, but it is present a millimetre away in the transverse dimensions of the closed string bulk. These models predict new forces at short distances mediated by superlight fields in the bulk, such as scalar or vector fields. The fields are massless in the absence of branes and acquire tiny masses due to non-supersymmetric radiative corrections from the branes, of the order of TeV2/MPlanck ~ 10-4 eV, corresponding to wavelengths in the submillimetre range. Such forces can be observable in microgravity experiments for any number of extra dimensions, in contrast to the deviation from Newton’s law, which is testable only in the two-dimensional case. As an example, figure 6 shows the prediction for a hypothetical scalar universal force mediated by a particle known as the radion.
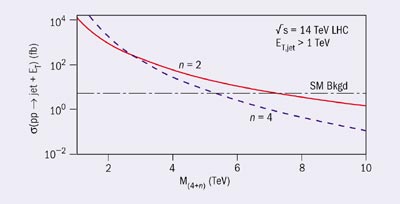
At particle colliders, there are generically three types of new phenomena associated with the existence of transverse and parallel dimensions, as well as with the string substructure of matter. Transverse dimensions are responsible for making gravity strong at TeV energies, and their main manifestation is through gravitational radiation in the bulk from any physical process that escapes detection and leads to events with missing energy (I Antoniadis et al. 1998, G F Giudice et al. 1999, E A Mirabelli et al. 1999). In contrast to microgravity experiments, high-energy particle accelerators, such as the LHC, are expected to produce a quasi-continuum of Kaluza-Klein excitations describing the propagation of the graviton to extra dimensions. Figure 7 shows the expected cross-section (number of events) at the LHC for the production of a single hadronic jet accompanied by missing energy due to graviton emission. Analysis of the angular distribution allows the spin of the unobserved graviton to be deduced, and these events to be differentiated from other possible sources of missing energy, such as the production of the lightest superparticle in supersymmetry.
Parallel dimensions of much smaller size, comparable to the string length, are manifest through the production of heavy Kaluza-Klein excitations for the photon and the mediators of the other Standard Model interactions. The LHC cannot miss these if their mass is below around 6 TeV, as figure 8 indicates (I Antoniadis and K Benakli 1994, I Antoniadis et al. 1994, 1999).

Finally, the string substructure of matter leads to spectacular new phenomena if the LHC centre-of-mass energy happens to be above the string scale. Some examples are the production of higher string excitations or even of micro-black holes weighing a few TeV. It is certain that in this case particle accelerators will become the best tools for studying quantum gravity in the laboratory.
Clearly, these theories exist only in our imagination at present. However, we look forward to the next generation of high-energy experiments and in particular to the most powerful machine, the LHC. I am convinced, as are the majority of my colleagues, that the LHC will play a very important role in the future of the high-energy physics of fundamental interactions. In fact, the LHC is designed to explore the origin of mass of elementary particles and in particular is designed to test the idea of supersymmetry, looking for the production of superparticles. We now hope that this accelerator may discover more spectacular and “exotic” phenomena, such as the existence of large extra dimensions of space and of fundamental strings.
Further reading
I Antoniadis 1990 Phys. Lett. B246 377.
I Antoniadis et al. 1994 Phys. Lett. B331 313.
I Antoniadis and K Benakli 1994 Phys. Lett. B326 69 (www.arxiv.org/abs/hep-th/9310151).
I Antoniadis et al. 1998 Phys. Lett. B436 263 (hep-ph/9804398).
I Antoniadis et al. 1999 Phys. Lett. B460 176 (hep-ph/9403290 ).
N Arkani-Hamed et al. 1998 Phys. Lett. B429 263 (hep-ph/9803315 ).
G F Giudice et al. 1999 Nucl. Phys. B544 3 (hep-ph/9811291).
M B Green et al. 1987 Superstring Theory, Vols 1 & 2 (Cambridge University Press).
C D Hoyle et al. 2001 Phys. Rev. Lett. 86 1418 (hep-ph/0011014 ).
T Kaluza 1921 Preuss. Akad. Wiss. 966.
O Klein 1926 Z. Phys. 37 895.
J C Long et al. 2002 hep-ph/0210004 (and references therein).
J D Lykken 1996 Phys. Rev. D54 3693 (hep-th/9603133).
E A Mirabelli et al. 1999 Phys. Rev. Lett. 82 2236 (hep-ph/9811337).
J Polchinski 1995 Phys. Rev. Lett. 75 4724 (hep-th/9510017).
E Witten 1995 Nucl. Phys. B443 85 (hep-th/9503124).