Physics Archives – Page 4 of 142

A step towards the Higgs self-coupling

ATLAS figure 1 — **Fig. 1.** (Top) Observed and expected statistical significances of Higgs-boson pair production in the HH → bbγγ channel from Run 2 and Run 3 data, and their combination. (Bottom) Likelihood scan of the Higgs-boson self-coupling modifier, showing observed and expected limits at 68% and 95% confidence levels (CL). Credit: ATLAS Collab, adapted from arXiv: 2507.03495

A defining yet unobserved property of the Higgs boson is its ability to couple to itself. The ATLAS collaboration has now set new bounds on this interaction, by probing the rare production of Higgs-boson pairs. Since the self-coupling strength directly connects to the shape of the Higgs potential, any departure from the Standard Model (SM) prediction would have direct implications for electroweak symmetry breaking and the early history of the universe. This makes its measurement one of the most important objectives of modern particle physics.

Higgs-boson pair production is a thousand times less frequent than single-Higgs events, roughly corresponding to a single occurrence every three trillion proton–proton collisions at the LHC. Observing such a rare process demands both vast datasets and highly sophisticated analysis techniques, along with the careful choice of a sensitive probe. Among the most effective is the HH → bbγγ channel, where one Higgs boson decays into a bottom quark–antiquark pair and the other into two photons. This final state balances the statistical reach of the dominant Higgs decay to bottom quarks with the exceptionally clean signature offered by photon-pair measurements. Despite the small signal branching ratio of about 0.26%, the decay to two photons benefits from the excellent di-photon mass resolution and offers the highest efficiency among the leading HH channels. This provides the HH → bbγγ channel with an excellent sensitivity to variations in the trilinear self-coupling modifier κ_λ, defined as the ratio of the measured Higgs-boson self-coupling to the SM prediction.

In its new study, the ATLAS collaboration relied on Run 3 data collected between 2022 and 2024, and on the full Run 2 dataset, reaching an integrated luminosity of 308 fb^–1. Events were selected with two high-quality photons and at least two b-tagged jets, identified using the latest and most performant ATLAS b-tagging algorithm. To further distinguish signal from background, dominated by non-resonant γγ+jets and single-Higgs production with H → γγ, a set of machine-learning classifiers called “multivariate analysis discriminants” were trained and used to filter genuine HH → bbγγ signals.

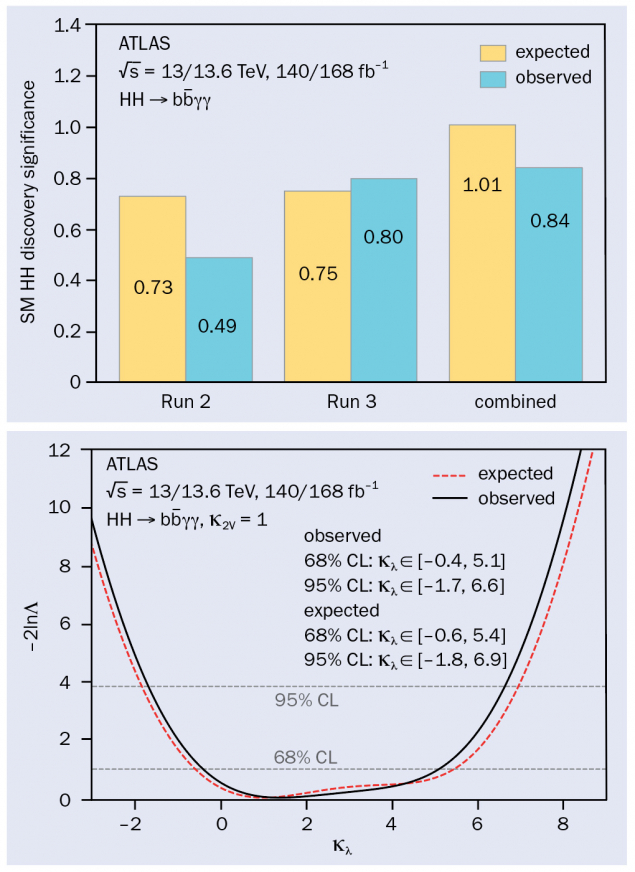
The collaboration reported an HH → bbγγ signal significance of 0.84σ under the background-only hypothesis, compared to a SM expectation of 1.01σ (see figure 1). At the 95% confidence level, the self-coupling modifier was constrained to –1.7 < κ_λ < 6.6. These results extend previous Run 2 analyses and deliver a substantially improved sensitivity, comparable to the observed (expected) significance of 0.4σ (1σ) in the combined Run 2 results across all channels. The improvement is primarily due to the adoption of advanced b-tagging algorithms, refined analysis techniques yielding better mass resolution and a larger dataset, more than double that of previous studies.

This result marks significant progress in the search for Higgs self-interactions at the LHC and highlights the potential of Run 3 data. With the full Run 3 dataset and the High-Luminosity LHC on the horizon, ATLAS is set to extend these measurements – improving our understanding of the Higgs boson and searching for possible signs of physics beyond the SM.

ALICE observes ρ–proton attraction

ALICE figure 1 — **Fig. 1.** The measured ρ⁰–proton correlation in high-multiplicity pp collisions. The suppression of ρ⁰–proton pairs at low relative momenta indicates an attractive interaction consistent with theoretical predictions. Credit: ALICE Collab. 2025 arXiv:2508.09867

The ALICE collaboration recently obtained the first direct measurement of the attraction between a proton and a ρ⁰ meson – a particle of particular interest due to its fleeting lifetime and close link to chiral symmetry breaking. The result establishes a technique known as femtoscopy as a new method for studying interactions between vector mesons and baryons, and opens the door to a systematic exploration of how short-lived hadrons behave.

Traditionally, interactions between baryons and vector mesons have been studied indirectly at low-energy facilities, using decay patterns or photoproduction measurements. These were mostly interpreted through vector–meson–dominance models developed in the 1960s, in which photons fluctuate into vector mesons to interact with hadrons. While powerful, these methods provide only partial information and cannot capture the full dynamics of the interaction. Direct measurements have long been out of reach, mainly because the extremely short lifetime of vector mesons – of the order of 1–10 fm/c – renders conventional scattering experiments impossible.

At the hadronic level, the strong force can be described as arising from the exchange of massive mesons, with the lightest among them, the pion, setting the interaction range to about 1.4 fm. For such a short-range effect to influence the products of a pp collision, the particles must be created close together and with low relative momentum, ensuring sufficient interaction time and a significant wavefunction overlap.

The ALICE collaboration has now studied this mechanism in high-multiplicity proton–proton (pp) collisions, at a centre-of-mass energy of 13 TeV, through femtoscopy, which examines correlations in the relative momentum (k^*) of particle pairs in their rest frame. These were expected to carry information on the size and shape of the particle-emitting source at k^* below about 200 MeV, with any deviations from unity indicating the presence of short-ranged forces.

To study the interaction between protons and ρ⁰ vector mesons, candidates were reconstructed via the hadronic decay channel ρ⁰ → π⁺π^–, identified from π⁺π^– pairs within the 0.70–0.85 GeV invariant mass window. Since the ρ⁰ decays almost instantly into pions, only about 3% of the candidates were genuine ρ⁰ mesons. Background corrections were therefore essential to extract the ρ⁰–proton correlation function, defined as the ratio of the relative-momentum distribution of same-event pairs to that of mixed-event pairs. The result is consistent with unity at large relative momenta (k^* > 200 MeV), as expected in the absence of strong forces. At lower values, however, a suppression with significance of about four standard deviations clearly signals ρ⁰–proton final-state interactions (see figure 1).

To interpret these results, ALICE used an effective field model based on chiral perturbation theory, which predicted two resonance states consistent with the formation of excited nucleon states. Because some pairs linger in these quasi-bound states instead of flying out freely, fewer emerge with nearly the same momentum. This results in a correlation suppression at low k^* consistent with observations. Unlike photoproduction experiments and QCD sum rules, femtoscopy delivers the complete phase information of the ρ⁰–proton interaction. By analysing both ρ–proton and φ–proton pairs, ALICE extracted precise scattering parameters that can now be incorporated into theoretical models.

This measurement sets a benchmark for vector-meson–dominance models and establishes femtoscopy as a tool to probe interactions involving the shortest-lived hadrons, while providing essential input for understanding ρ–nucleon interactions in vacuum and describing the meson’s properties in heavy-ion collisions. Pinning down how the ρ meson behaves is crucial for interpreting dilepton spectra and the restoration of chiral symmetry, as differences between light quark masses become negligible at high energies. For example, the mass gap between the ρ and its axial counterpart, a₁, comes from spontaneous chiral-symmetry breaking.

The measurement problem, measured

A century on, physicists still disagree on what quantum mechanics actually means. Nature recently surveyed more than a thousand researchers, asking about their views on the interpretation of quantum mechanics. When broken down by career stage, the results show that a diversity of views spans all generations.

**Getting eccentric with age** Preferred interpretation of quantum mechanics by career stage. “Epistemic or QBism” respondents regard the quantum state as representing knowledge or belief rather than an objective property of nature. “Everett” includes many-worlds quantum mechanics and consistent histories. “Other” groups less common responses, such as retrocausal and superdeterministic models, while “none” includes those who selected “Shut up and calculate.” Credit: *Nature*/D De Biasio

The Copenhagen interpretation remains the most widely held view, placing the act of measurement at the core of quantum theory well into the 2020s. Epistemic or QBist approaches, where the quantum state expresses an observer’s knowledge or belief, form the next most common group, followed by Everett’s many-worlds framework, in which all quantum outcomes continue to coexist without collapse (CERN Courier July/August 2025 p26). Other views maintain small but steady followings, including pilot-wave theory, spontaneous-collapse models and relational quantum mechanics (CERN Courier July/August 2025 p21).

Fewer than 10% of physicists surveyed declined to express a view. Though this cohort purports to include proponents of the “shut up and calculate” school of thought, an apparently dwindling cohort of disinterested working physicists may simply be undersampled.

Crucially, confidence is modest. Most respondents view their preferred interpretation as an adequate placeholder or a useful conceptual tool. Only 24% are willing to describe their preferred interpretation as correct, leaving ample room for manoeuvre in the very foundations of fundamental physics.

Neural networks boost B-tagging

LHCb figure 1 — **Fig. 1.** Tagging power as a function of the transverse momentum of the neutral B-meson, measured with 5.4 fb^–1 of LHCb data for B⁰_s → D^–_s π⁺ decays. The inclusive flavour tagger (blue) outperforms the combination of opposite- and same-side taggers (red). Credit: LHCb Collab. arXiv:2508.20180

The LHCb collaboration has developed a new inclusive flavour-tagging algorithm for neutral B-mesons. Compared to standard approaches, it can correctly identify 35% more B⁰ and 20% more B⁰_s decays, expanding the dataset available for analysis. This increase in tagging power will allow for more accurate studies of charge–parity (CP) violation and B-meson oscillations.

In the Standard Model (SM), neutral B-mesons oscillate between particle and antiparticle states via second-order weak interactions involving a pair of W-bosons. Flavour-tagging techniques determine whether a neutral B-meson was initially produced as a B⁰ or its antiparticle B⁰, thereby enabling the measurement of time-dependent CP asymmetries. As the initial flavour can only be inferred indirectly from noisy, multi-particle correlations in the busy hadronic environment of the LHC, mistag rates have traditionally been high.

Until now, the LHCb collaboration has relied on two complementary flavour-tagging strategies. One infers the signal meson’s flavour by analysing the decay of the other b-hadron in the event, whose existence follows from bb– pair production in the original proton-proton collision. Since the two hadrons originate from oppositely-charged, early-produced bottom quarks, the method is known as “opposite-side” (OS) tagging. The other strategy, or “same-side” (SS) tagging, uses tracks from the fragmentation process that produced the signal meson. Each provides only part of the picture, and their combination defined the state of the art in previous analyses.

The new algorithm adopts a more comprehensive approach. Using a deep neural network based on the “DeepSets” architecture, it incorporates information from all reconstructed tracks associated with the hadronisation process, rather than preselecting a subset of candidates. By considering the global structure of the event, the algorithm builds a more detailed inference of the meson’s initial flavour. This inclusive treatment of the available information increases both the sensitivity and the statistical reach of the tagging procedure.

The model was trained and calibrated using well-established B⁰ and B⁰_s meson decay channels. When compared with the combination of opposite-side and same-side taggers, the inclusive algorithm displayed a 35% increase in tagging power for B⁰ mesons and 20% for B⁰_s mesons (see figure 1). The improvement stems from gains in both the fraction of events that receive a flavour tag and how often the tag is correct. Tagging power is a critical figure of merit, as it determines the effective amount of usable data. Therefore, even modest gains can dramatically reduce statistical uncertainties in CP-violation and B-oscillation measurements, enhancing the experiment’s precision and discovery potential.

This development illustrates how algorithmic innovation can be as important as detector upgrades in pushing the boundaries of precision. The improved tagging power effectively expands the usable data sample without requiring additional collisions, enhancing the experiment’s capacity to test the SM and seek signs of new physics within the flavour sector. The timing is particularly significant as LHCb enters Run 3 of the LHC programme, with higher data rates and improved detector components. The new algorithm is designed to integrate smoothly with existing reconstruction and analysis frameworks, ensuring immediate benefits while providing scalability for the much larger datasets expected in future runs.

As the collaboration accumulates more data, the inclusive flavour-tagging algorithm is likely to become a central tool in data analysis. Its improved performance is expected to reduce uncertainties in some of the most sensitive measurements carried out at the LHC, strengthening the search for deviations from the SM.

NuFact prepares for a precision era

The 26th edition of the International Workshop on Neutrinos from Accelerators (NuFact) attracted more than 200 physicists to Liverpool from 1 to 6 September. There was no shortage of topics to discuss. Delegates debated oscillations, scattering, accelerators, muon physics, beyond-PMNS physics, detectors, and inclusion, diversity, equity, education and outreach (IDEEO).

Neutrino physics has come a long way since the discovery of neutrino oscillations in 1998. Experiments now measure oscillation parameters with a precision of a few per cent. At NuFact 2025, the IceCube collaboration reported new oscillation measurements using atmospheric neutrinos from 11 years of observations at the South Pole. The measurements achieve world-leading sensitivity on neutrino mixing angles, alongside new constraints on the unitarity of the neutrino mixing matrix. Meanwhile, the JUNO experiment in China celebrated the start of data-taking with its liquid-scintillator detector (see “JUNO takes aim at neutrino-mass hierarchy”). JUNO will determine the neutrino mass ordering by observing the fine oscillation patterns of antineutrinos produced in nuclear reactors.

Neutrino scattering

Beyond oscillations, a major theme of the conference was neutrino scattering. Although neutrinos are the most abundant massive particles in the universe, their interactions with matter remain poorly understood. Measuring and modelling these processes is essential: they probe nuclear structure and hadronic physics in a novel way, while also providing the foundation for oscillation analyses in current and next-generation experiments. Exciting advances were reported across the field. The SBND experiment at Fermilab announced the collection of around three million neutrino interactions using the Booster Neutrino Beam. ICARUS presented its first neutrino–argon cross-section measurement. MicroBooNE, MINERvA and T2K showcased new results on neutrino–nucleus interaction and compared them with theoretical models. The e4ν collaboration highlighted electron beams as potential sources of data to refine neutrino-scattering models, supporting efforts to achieve the detailed interaction picture needed for the coming precision era of oscillation physics. At higher energies, FASER and SND@LHC showcased their LHC neutrino observations with both emulsion and electronic detectors.

Neutrino physics is one of the most vibrant and global areas of particle physics today

CERN’s role in neutrino physics was on display throughout the conference. Beyond the results from ICARUS, FASER and SND@LHC, other contributions included the first observation of neutrinos in the ProtoDUNE detectors, the status of the MUonE experiment – aimed at measuring the hadronic contribution to the muon anomalous magnetic moment – and the latest results from NA61. The role of CERN’s Neutrino Platform was also highlighted in contributions about the T2K ND280 near-detector upgrade and the WAGASCI–BabyMIND detector, both of which were largely assembled and tested at CERN. Discussions featured the results of the Water Cherenkov Test Experiment, which operated in the T9 beamline to prototype technology for Hyper-Kamiokande, and other novel CERN-based ideas, such as nuSCOPE – a proposal for a short-baseline experiment that would “tag” individual neutrinos at production, formed from the merging of ENUBET and NuTag. Building on a proof-of-principle result from NA62, which identified a neutrino candidate via its parent kaon decay, this technique could represent a paradigm shift in neutrino beam characterisation.

NuFact 2025 reinforced the importance of diversity and inclusion in science. The IDEEO working group led discussions on how varied perspectives and equitable participation strengthen collaboration, improve problem solving and attract the next generation of researchers. Dedicated sessions on education and outreach also highlighted innovative efforts to engage wider communities and ensure that the future of neutrino physics is both scientifically robust and socially inclusive. From precision oscillation measurements to ambitious new proposals, NuFact 2025 demonstrated that neutrino physics is one of the most vibrant and global areas of particle physics today.

Mainz muses on future of kaon physics

The 13th KAONS conference convened almost 100 physicists in Mainz from 8 to 12 September. Since the first edition took place in Vancouver in 1988, the conference series has returned roughly every three years to bring together the global kaon-physics community. This edition was particularly significant, being the first since the decision not to continue CERN’s kaon programme with the proposed HIKE experiment (CERN Courier May/June 2024 p7).

CERN’s current NA62 effort was nevertheless present in force. Eight presentations spanned its wide-ranging programme, from precision studies of rare kaon decays to searches for lepton-flavour and lepton-number violation, and explorations beyond the Standard Model (SM). Complementary perspectives came from Japan’s KOTO experiment at J-PARC, from multipurpose facilities such as KLOE-2, Belle II and CERN’s LHCb experiment, as well as from a large and engaged theoretical community. Together, these contributions underscored the vitality of kaon physics: a field that continues to test the SM at the highest levels of precision, with a strong potential to uncover new physics.

NA62 reported a big success on the so-called “golden mode” ultra-rare decay K⁺ → π⁺νν, a process that is highly sensitive to new physics (CERN Courier July/August 2024 p30). NA62 has already delivered remarkable progress in this domain: by analysing data up to 2022, the collaboration more than doubled its sample from 20 to 51 candidate events, achieving the first 5σ observation of the decay (CERN Courier November/December 2024 p11). This is the smallest branching fraction ever measured, and, intriguingly, shows a mild 1.7σ tension with the Standard Model prediction, which itself is known with a 2% theoretical uncertainty. With the experiment continuing to collect data until CERN’s next long shutdown (LS3), NA62’s final dataset is expected to triple the current statistics, sharpening what is already one of the most stringent tests of the SM.

Another major theme was the study of rare B-meson decays where kaons often appear in the final state, for example B → K^* (→ Kπ) ℓ⁺ℓ^–. Such processes are central to the long-debated “B anomalies,” in which certain branching fractions of rare semileptonic B decays show persistent tensions between experimental results and SM predictions (CERN Courier January/February 2025 p14). On the experimental front, CERN’s LHCb experiment continues to lead the field, delivering branching-fraction measurements with unprecedented precision. Progress is also being made on the theoretical side, though significant challenges remain in matching this precision. The conference highlighted new approaches reducing uncertainties and biases, based both on phenomenological techniques and lattice QCD.

Kaon physics is in a particularly dynamic phase. Theoretical predictions are reaching unprecedented precision, and two dedicated experiments are pushing the frontiers of rare kaon decays. At CERN, NA62 continues to deliver impactful results, even though plans for a next-stage European successor did not advance this year. Momentum is building in Japan, where the proposed KOTO-II upgrade, if approved, would secure the long-term future of the programme. Just after the conference, the KOTO-II collaboration held its first in-person meeting, bringing together members from both KOTO and NA62 – a promising sign for continued cross-fertilisation. Looking ahead, sustaining two complementary experimental efforts remains highly desirable: independent cross-checks and diversified systematics. Both will be essential to fully exploit the discovery potential of rare kaon decays.

Invisibles, in sight

Around 150 researchers gathered at CERN from 1 to 5 September to discuss the origin of the observed matter–antimatter asymmetry in the universe, the source of its accelerated expansion, the nature of dark matter and the mechanism behind neutrino masses. The vibrant atmosphere of the annual meeting of the Invisibles research network encouraged lively discussions, particularly among early-career researchers.

Marzia Bordone (University of Zurich) highlighted central questions in flavour physics, such as the tensions in the determinations of quark flavour-mixing parameters and the anomalies in leptonic and semileptonic B-meson decays (CERN Courier January/February 2025 p14). She showed that new bosons beyond the Standard Model that primarily interact with the heaviest quarks are theoretically well motivated and could be responsible for these flavour anomalies. Bordone emphasised that collaboration between experiment and theory, as well as data from future colliders like FCC-ee, will be essential to understand whether these effects are genuine signs of new physics.

Lina Necib (MIT) shared impressive new results on the distribution of galactic dark matter. Though invisible, dark matter interacts gravitationally and is present in all galaxies across the universe. Her team used exquisite data from the ESA Gaia satellite to track stellar trajectories in the Milky Way and determine the local dark-matter distribution to within 20–30% precision – which means about 300,000 dark-matter particles per cubic metre assuming they have mass similar to that of the proton. This is a huge improvement over what could be done just one decade ago, and will aid experiments in their direct search for dark matter in laboratories worldwide.

The most quoted dark-matter candidates at Invisibles25 were probably axions: particles once postulated to explain why the strong interactions that bind protons and neutrons behave in the same way for particles and antiparticles. Nicole Righi (King’s College London) discussed how these particles are ubiquitous in string theory. According to Righi, their detection may imply a hot Big Bang, with a rather late thermal stage, or hint at some special feature of the geometry of ultracompact dimensions related to quantum gravity.

The most intriguing talk was perhaps the CERN colloquium given by the 2011 Nobel laureate Adam Riess (Johns Hopkins University). By setting up an impressive system of distance measurements to extragalactic systems, Riess and his team have measured the expansion rate of the universe – the Hubble constant – with per cent accuracy. Their results indicate a value about 10% higher than that inferred from the cosmic microwave background within the standard ΛCDM model, a discrepancy known as the “Hubble tension”. After more than a decade of scrutiny, no single systematic error appears sufficient to account for it, and theoretical explanations remain tightly constrained (CERN Courier March/April 2025 p28). In this regard, Julien Lesgourgues (RWTH Aachen University) pointed out that, despite the thousands of papers written on the Hubble tension, there is no compelling extension of ΛCDM that could truly accommodate it.

While 95% of the universe’s energy density is invisible, the community studying it is very real. Invisibles now has a long history and is based on three innovative training networks funded by the European Union, as well as two Marie Curie exchange networks. The network includes more than 100 researchers and 50 PhD students spread across key beneficiaries in Europe, as well as America, Asia and Africa – CERN being one of their long-term partners. The energy and enthusiasm of the participants at this conference were palpable, as nature continues to offer deep mysteries that the Invisibles community strives to unravel.

Higgs hunters revel in Run 3 data

The 15th Higgs Hunting workshop took place from 15 to 17 July at IJCLab in Orsay and LPNHE in Paris. It offered an opportunity to about 100 participants to step back and review the most recent LHC Run 2 and 3 Higgs-boson results, together with some of the latest theoretical developments.

One of the highlights concerned the Higgs boson’s coupling to the charm quark, with the CMS collaboration presenting a new search using Higgs production in association with a top–antitop pair. The analysis, targeting Higgs decays into charm–quark pairs, reached a sensitivity comparable to the best existing direct constraints on this elusive interaction. New ATLAS analyses showcased the impact of the large Run 3 dataset, hinting at great potential for Higgs physics in the years to come – for example, Run 3 data has reduced the uncertainties on the coupling of the Higgs boson to muons and Zγ by 30% and 38%, respectively. On the di-Higgs front, the expected upper limit on the signal-strength modifier, measured in the bbγγ final state only, has now surpassed in sensitivity the combination of all Run 2 HH channels (see “A step towards the Higgs self-coupling”). The sensitivity to di-Higgs production is expected to improve significantly during Run 3, raising hopes of seeing a signal before the next long shutdown, from mid-2026 to the end of 2029.

Juan Rojo (Vrije Universiteit Amsterdam) discussed parton distribution functions for Higgs processes at the LHC, while Thomas Gehrmann (University of Zurich) reviewed recent developments in general Higgs theory. Mathieu Pellen (University of Freiburg) provided a review of vector-boson fusion, Jose Santiago Perez (University of Granada) summarised the effective field theory framework and Oleksii Matsedonskyi (University of Cambridge) reviewed progress on electroweak phase transitions. In his “vision” talk, Alfredo Urbano (INFN Rome) discussed the interplay between Higgs physics and early-universe cosmology. Finally, Benjamin Fuks (LPTHE, Sorbonne University) presented a toponium model, bringing the elusive romance of top–quark pairs back into the spotlight (CERN Courier September/October 2025 p9).

After a cruise on the Seine in the light of the Olympic Cauldron, participants were propelled toward the future during the European Strategy for Particle Physics session. The ESPPU secretary Karl Jakobs (University of Freiburg) and various session speakers set the stage for spirited and vigorous discussions of the options before the community – in particular, the scenarios to pursue should the FCC programme, the clear plan A, not be realised. The next Higgs Hunting workshop will be held in Orsay and Paris from 16 to 18 September 2026.

All aboard the scalar adventure

Since the discovery of the Higgs boson in 2012, the ATLAS and CMS collaborations have made significant progress in scrutinising its properties and interactions. So far, measurements are compatible with an elementary Higgs boson, originating from the minimal scalar sector required by the Standard Model. However, current experimental precision leaves ample room for this picture to change. In particular, the full potential of the LHC and its high-luminosity upgrade to search for a richer scalar sector beyond the Standard Model (BSM) is only beginning to be tapped.

The first Workshop on the Impact of Higgs Studies on New Theories of Fundamental Interactions, which took place on the Island of Capri, Italy, from 6 to 10 October 2025, gathered around 40 experimentalists and theorists to explore the pivotal role of the Higgs boson in exploring BSM physics. Participants discussed the implications of extended scalar sectors and the latest ATLAS and CMS searches, including current potential anomalies in LHC data.

“The Higgs boson has moved from the realm of being just a new particle to becoming a tool for searches for BSM particles,” said Greg Landsberg (Brown University) in an opening talk.

An extended scalar sector can address several mysteries in the SM. For example, it could serve as a mediator to a hidden sector that includes dark-matter particles, or play a role in generating the observed matter–antimatter asymmetry during an electroweak phase transition. Modified or extended Higgs sectors also arise in supersymmetric and other BSM models that address why the 125 GeV Higgs boson is so light compared to the Planck mass – despite quantum corrections that should drive it to much higher scales – and might shed light on the perplexing pattern of fermion masses and flavours.

One way to look for new physics in the scalar sector is modifications in the decay rates, coupling strengths and CP-properties of the Higgs boson. Another is to look for signs of additional neutral or charged scalar bosons, such as those predicted in longstanding two-Higgs-doublet or Higgs-triplet models. The workshop saw ATLAS and CMS researchers present their latest limits on extended Higgs sectors, which are based on an increasing number of model-independent or signature-based searches. While the data so far are consistent with the SM, a few mild excesses have attracted the attention of some theorists.

In diphoton final states, a slight excess of events persists in CMS data at a mass of 95 GeV. Hints of a small excess at a mass of 152 GeV are also present in ATLAS data, while a previously reported excess at 650 GeV has faded after full examination of Run 2 data. Workshop participants also heard suggestions that the Brout–Englert–Higgs potential could allow for a second resonance at 690 GeV.

The High-Luminosity LHC will enable us to explore the scalar sector in detail

“We haven’t seen concrete evidence for extended Higgs sectors, but intriguing features appear in various mass scales,” said CMS collaborator Sezen Sekmen (Kyungpook National University). “Run 3 ATLAS and CMS searches are in full swing, with improved triggering, object reconstruction and analysis techniques.”

Di-Higgs production, the rate of which depends on the strength of the Higgs boson’s self-coupling, offers a direct probe of the shape of the Brout–Englert–Higgs potential and is a key target of the LHC Higgs programme. Multiple SM extensions predict measurable effects on the di-Higgs production rate. In addition to non-resonant searches in di-Higgs production, ATLAS and CMS are pursuing a number of searches for BSM resonances decaying into a pair of Higgs bosons, which were shown during the workshop.

Rich exchanges between experimentalists and theorists in an informal setting gave rise to several new lines of attack for physicists to explore further. Moreover, the critical role of the High-Luminosity LHC to probe the scalar sector of the SM at the TeV scale was made clear.

“Much discussed during this workshop was the concern that people in the field are becoming demotivated by the lack of discoveries at the LHC since the Higgs, and that we have to wait for a future collider to make the next advance,” says organiser Andreas Crivellin (University of Zurich). “Nothing could be further from the truth: the scalar sector is not only the least explored of the SM and the one with the greatest potential to conceal new phenomena, but one that the High-Luminosity LHC will enable us to explore in detail.”

Subtleties of quantum fields

Quantum field theory unites quantum physics with special relativity. It is the framework of the Standard Model (SM), which describes the electromagnetic, weak and strong interactions as gauge forces, mediated by photons, gluons and W and Z bosons, plus additional interactions mediated by the Higgs field. The success of the SM has exceeded all expectations, and its mathematical structure has led to a number of impressive predictions. These include the existence of the charm quark, discovered in 1974, and the existence of the Higgs boson, discovered in 2012.

Uncovering Quantum Field Theory and the Standard Model by Wolfgang Bietenholz of the National Autonomous University of Mexico and Uwe-Jens Wiese from the University of Bern, explains the foundations of quantum field theory in great depth, from classical field theory and canonical quantisation to regularisation and renormalisation, via path integrals and the renormalisation group. What really makes the book special are frequently discussed relations to statistical mechanics and condensed-matter physics.

Riding a wave

The section on particles and “wavicles” is highly original. In quantum field theory, quantised excitations of fields cannot be interpreted as point-like particles. Unlike massive particles in non-relativistic quantum mechanics, these excitations have non-trivial localisation properties, which apply to photons and electrons alike. To emphasise the difference between non-relativistic particles and wave excitations in a relativistic theory, one may refer to them as “wavicles”, following Frank Wilczek. As discussed in chapter 3, an intuitive understanding of wavicles can be gained by the analogy to phonons in a crystal. Another remarkable feature of charged fields is the infinite extension of their excitations due to their Coulomb field. This means that any charged state necessarily includes an infrared cloud of soft gauge bosons. As a result, they cannot be described by ordinary one-particle states and are referred to as “infraparticles”. Their properties, along with the related “superselection sectors,” are explained in the section on scalar quantum electrodynamics.

Uncovering Quantum Field Theory and the Standard Model — Credit: Cambridge University Press

The SM can be characterised as a non-abelian chiral gauge theory. Bietenholz and Wiese explain the various aspects of chirality in great detail. Anomalies in global and local symmetries are carefully discussed in the continuum as well as on a space–time lattice, based on the Ginsparg–Wilson relation and Lüscher’s lattice chiral symmetry. Confinement of quarks and gluons, the hadron spectrum, the parton model and hard processes, chiral perturbation theory and deconfinement at high temperatures uncover perturbative and non-perturbative aspects of quantum chromodynamics (QCD), the theory of strong interactions. Numerical simulations of strongly coupled lattice Yang–Mills theories are very demanding. During the past four decades, much progress has been made in turning lattice QCD into a quantitative reliable tool by controlling statistical and systematic uncertainties, which is clearly explained to the critical reader. The treatment of QCD is supplemented by an introduction to the electroweak theory covering the Higgs mechanism, electroweak symmetry breaking and flavour physics of quarks and leptons.

The number of quark colours, which is three in nature, plays a prominent role in this book. At the quantum level, gauge symmetries can fail due to anomalies, rendering a theory inconsistent. The SM is free of anomalies, but this only works because of a delicate interplay between quark and lepton charges and the number of colours. An important example of this interplay is the decay of the neutral pion into two photons. The subtleties of this process are explained in chapter 24.

The number of quark colours, which is three in nature, plays a prominent role in this book

Most remarkably, the SM predicts baryon-number-violating processes. This arises from the vacuum structure of the weak SU(2) gauge fields, which involves topologically distinct field configurations. Quantum tunnelling between them, together with the anomaly in the baryon–number current, leads to baryon–number violating transitions, as discussed in chapter 26. Similarly, in QCD a non-trivial topology of the gluon field leads to an explicit breaking of the flavour-singlet axial symmetry and, subsequently, to the mass of the η′ meson. Moreover, the gauge field topology gives rise to an additional parameter in QCD, the vacuum-angle θ. Since this parameter induces an electric dipole moment of the neutron that satisfies a strong upper bound, this confronts us with the strong-CP problem: what constrains θ to be so tiny that the experimental upper bound on the neutron dipole moment is satisfied? A solution may be provided by the Peccei–Quinn symmetry and axions, as discussed in a dedicated chapter.

By analogy with the QCD vacuum angle, one can introduce a CP-violating electromagnetic parameter θ into the SM – even though it has no physical effect in pure QED. This brings us to a gem of the book: its discussion of the Witten effect. In the presence of such a θ, the electric charge of a magnetic monopole becomes θ/2π plus an integer. This leads to the remarkable conclusion that for non-zero θ, all monopoles become dyons, carrying both electric and magnetic charge.

The SM is an effective low-energy theory and we do not know at what energy scale elements of a more fundamental theory will become visible. Its gauge structure and quark and lepton content hint at a possible unification of the interactions into a larger gauge group, which is discussed in the final chapter. Once gravity is included, one is confronted with a hierarchy problem: the question of why the electroweak scale is so small compared to the Planck mass, at which the Compton wavelength of a particle and its Schwarzschild radius coincide. Hence, at Planck energies quantum gravitational effects cannot be ignored. Perhaps, solving the electroweak hierarchy puzzle requires working with supersymmetric theories. For all students and scientists struggling with the SM and exploring possible extensions, the nine appendices will be a very valuable source of information for their research.

Topics

Reset your password

Registration complete

Neutrino scattering

Riding a wave