Finding a quantum field theory that includes gravity has eluded the best minds of physics. Yaron Oz of CERN explains how the theory of superstrings modifies classical geometry, and how the secrets of quantum black holes are encoded in quantum field theories. Remarkable new developments show how physical field theories, such as that of quarks and gluons, can be related to gravity in higher dimensions.
Quantum field theories have had great success in describing elementary particles and their interactions, and a continual objective has been to apply these successful methods to gravity as well.
The natural length scale for quantum gravity to be important is the Planck length, lp: 1.6 x 10-33 cm. The corresponding energy scale is the Planck mass, Mp: 1.2 x 1019 GeV. At this scale the effect of gravity is comparable to that of other forces and is the natural energy for the unification of gravity with other interactions. Evidently this energy is far beyond the reach of present accelerators. Thus, at least in the near future, experimental tests of a unified theory of gravity with the other interactions are bound to be indirect.
When we try to quantize the classical theory of gravity, we encounter short-distance (high-energy) divergences (infinities) that cannot be controlled by the standard renormalization schemes of quantum field theory. These have a physical meaning: they signal that the theory is only valid up to a certain energy scale. Beyond that there is new physics that requires a different description.
Quantum gravity
Such a phenomenon is not unfamiliar. The short-distance divergences of Fermi’s original theory of the weak interactions (with four particles meeting at one space-time point) signal that the description is only valid for energies less than the masses of the W and Z carrier particles. The divergences are resolved by introducing these particles in the Glashow-Salam-Weinberg theory.
We expect that the divergences of quantum gravity would similarly be resolved by introducing the correct short distance description that captures the new physics. Although years of effort have been devoted to finding such a description, only one candidate has emerged to describe the new short-distance physics: superstrings.
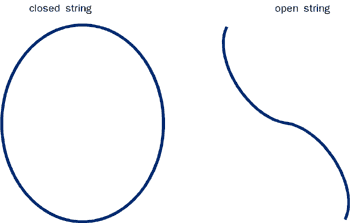
This theory requires radically new thinking. In superstring theory, the graviton (the carrier of the force of gravity) and all other elementary particles are vibrational modes of a string (figure 1). The typical string size is the Planck length, which means that, at the length scales probed by current experiments, the string appears point-like.
The jump from conventional field theories of point-like objects to a theory of one-dimensional objects has striking implications. The vibration spectrum of the string contains a massless spin-2 particle: the graviton. Its long wavelength interactions are described by Einstein’s theory of General Relativity. Thus General Relativity may be viewed as a prediction of string theory!
The quantum theory of strings, using an extended region of space-time, sidesteps short-distance divergences and provides a finite theory of quantum gravity. Besides the graviton, the vibration spectrum of the string contains other excited oscillators that have the properties of other gauge particles, the carriers of the various forces. This makes the theory a promising (and so far the only) candidate for a unification of all of the particle interactions with gravity.
In the absence of direct experimental data to confront string theory, research in this field is largely guided by the requirement for the internal consistency of the theory. This turns out to dictate very stringent constraints. Again, this is not unfamiliar to particle physicists. When resolving the short-distance divergences of Fermi weak interaction theory, the space-time and internal symmetries provide stringent constraints and guide us to the solution.
Superstring theories
Two important features of string theory are implied by the consistency requirement. First, superstring theory is consistent only in 9+1 space-time dimensions. This seems to contradict the fact that the world that we see has 3+1 space-time dimensions. Second, there are five consistent superstring theories: Type IIA, Type IIB, Type I, E8 x E8 Heterotic and S0(32) Heterotic. Type I is a theory of unoriented open and closed strings; the others are theories of oriented closed strings. Which should be preferred?
All five possess supersymmetry, hence the name superstrings. According to supersymmetry theory, any boson (integer spin particle) has a fermionic (half-integer) superpartner and vice versa. One way to view supersymmetric field theories is as field theories in superspace a space with extra fermionic quantum dimensions. Many physicists expect that supersymmetry exists at the tera electron volt scale, so that the new ‘superpartner’ particles could be seen by CERN’s LHC proton collider.
Compactification and stringy geometry
The time and the three spatial dimensions that we see are approximately flat and infinite. They are also expanding. Just after the Big Bang they were highly curved and small. It is possible that while these four dimensions expanded, other dimensions did not expand, remaining small and highly curved.
Superstring theory says that we live in 9+1 space-time dimensions, six of which are small and compact, while the time and three spatial dimensions have expanded and are infinite.
How can we see these extra six dimensions? As long as our experiments cannot reach the energies needed to probe such small distances, the world will look to us 3+1-dimensional and the extra dimensions can be probed only indirectly via their effect on 3+1-dimensional physics. It is not known at what energies the hidden compact dimensions will open up. The possibility that new dimensions or strings will be seen by the LHC is not ruled out by the current experimental data.
Superstring theory employs the KaluzaKlein mechanism to unify gravitation and gauge interactions using higher dimensions. In such theories the higher dimensional graviton field appears as a graviton, photon or scalar in the 3+1-dimensional world, depending on whether its spin is aligned along the infinite or compact dimensions.
The number of consistent compactifications of the extra six co-ordinates is large. Which compactification to choose is the prize question. The answer is hidden in the dynamics of superstring theory. Using a limited (perturbative) framework, one can attempt a qualitative study of the 3+1-dimensional phenomenology obtained from different compactifications. It is encouraging that some of these compactifications result in 3+1 dimensional models that have qualitative features such as gauge groups and matter representations of plausible grand unification models. Interestingly the low-mass fermions appear in families, the number of which is determined by the topology of the compact space.
T-duality
Not all of the compactifications are distinguishable. To illustrate this, take one spatial co-ordinate to be a circle of radius R. There are two types of excitations. The first, which is familiar from theories of point-like objects, results from the quantization of momentum along the circle. These are called KaluzaKlein excitations. The second type arises from the closed string winding around the circle. These are called winding mode excitations. This is a new feature that does not exist in point-like theories. When we map the size of the radius, R, of the circle to its inverse, 1/R, with the string scale set to one, the two types of excitations are exchanged and the theory remains invariant. There is no way to distinguish the compactification on a circle of radius R from a compactification on a circle of radius 1/R. This means that the classical geometrical concepts break down at short distances and the classical geometry is replaced by stringy geometry.
In physical terms, this implies a modification of the well known uncertainty principle. The spatial resolution, Dx , has a lower bound dictated not just by the inverse of the momentum spread, Dp, but also by the string size. The mapping of the radius of the compactification to its inverse, exchanging KaluzaKlein excitations with winding modes, is called T-duality.
Another example of stringy geometry is “mirror symmetry”. In the previous example, both circles had the same topology and different sizes. In contrast, mirror symmetry is an example of stringy geometry where two six dimensional spaces, called Calabi-Yau manifolds, with different topology are not distinguishable by the string probe.