Protons and neutrons cosy up in nuclei and neutron stars

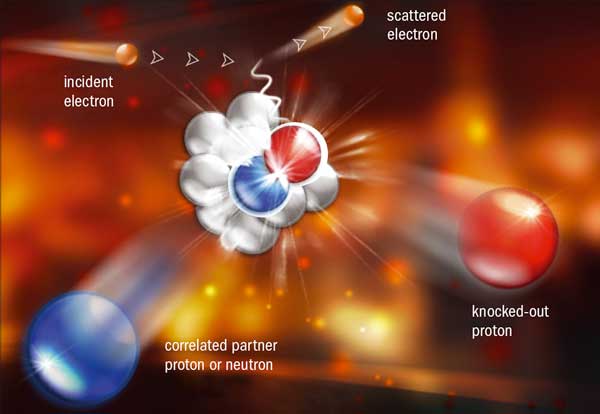
The structure of nuclei is determined by the nature of the strong force: strong repulsion at short distances and strong attraction at moderate distances. This force, which binds the nucleons together while also keeping the structure from collapsing, makes the nucleus a fairly dilute system. This has allowed for calculations that treat the nucleus as a collection of hard objects in an average or mean field to describe many of the properties of nuclear matter. Of course, this simple picture of the nucleus is inaccurate – the nucleons should really be thought of as waves that can strongly overlap for short periods of time. Indeed, recent experiments have shown that about 20% of all nucleons in carbon are in such a state at any given time.

These states of strongly overlapping wave functions are commonly referred to as nucleon–nucleon short-range correlations (SRC). Calculations indicate that, for short periods, these correlations lead to local densities in the nucleus that are several times as high as the average nuclear density of 0.17 GeV/fm³. Such densities are comparable to those predicted in the core of neutron stars. c– whether extremely small (such as helium nuclei) or extremely large (such as neutron stars).

The distinctive experimental features of two-nucleon SRCs are the large back-to-back relative momentum and small centre-of-mass momentum of the correlated pair, where large and small are relative to the Fermi-sea level of about 250 MeV/c. This is shown in figure 1, where a virtual photon is absorbed by one nucleon in a correlated pair, causing both nucleons to be emitted from the nucleus. The large strength of the nucleon–nucleon interaction at short distances means that the relative motion in the pair should be the same in all nuclei, although the absolute probability of a correlation grows with density – with the probability of a nucleon to be part of a pair reaching 25% for iron and heavier nuclei.

Scaling effects

Isolating the signal of the SRC initial state has been difficult at low and medium energies because other processes (such as final-state interactions and meson-exchange currents) mimic this effect. Nevertheless, there has recently been progress using modern accelerators with high-luminosity and high-momentum transfer – as well as with kinematics, where competing mechanisms are suppressed. For electron scattering, this corresponds to luminosities of 10³⁷ cm^–2s^–1; a four-momentum transfer, Q², greater than 1.4 (GeV/c)²; and focusing on kinematics where Bjorken-x, Q²/2mυ, is greater than 1, where υ is the beam energy minus the energy of the scattered electron. For elastic scattering from a free proton, Bjorken-x is exactly 1. At least two nucleons must be involved to have x > 1; x > 2 requires a system with at least three nucleons.

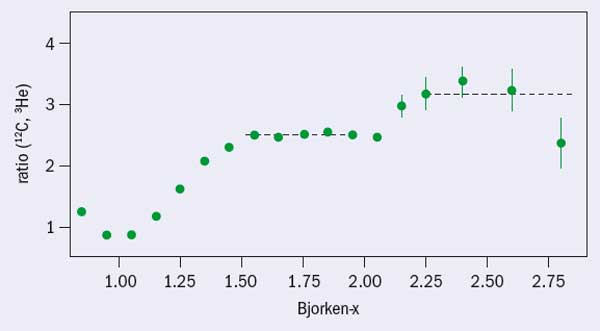
One of the new results has come from inclusive data at high momentum-transfer, Q² > 1.4 (GeV/c)², and x > 1 from the Hall B CEBAF Large Acceptance Spectrometer at the US Department of Energy’s Jefferson Laboratory (K S Egiyan et al. 2006). The measurement was made to check the predicted universality of SRCs by measuring the ratio of the inclusive cross-sections off heavy nuclei to those of light nuclei at sufficiently large Q² and x, where the scattering off slow nucleons in the nucleus does not contribute. The signal predicted to indicate dominance of such correlations is the scaling of the ratios – a weak dependence on x and Q² for 1 < x <2 – which is clearly observed in the data. Continuing this line of reasoning would suggest that a second scaling region arising from three-nucleon correlations should be observed for x > 2. Indeed, a second scaling region does seem to be present, although the statistics are limited (figure 2). These results reflect the dominance of few-nucleon correlations in the high-momentum component of the nucleus.

While the inclusive data clearly suggest strong local correlations, it has taken exclusive data to confirm that the inclusive scaling arises from SRCs, as well as to measure directly what fraction of nucleon-pair types are involved. In exclusive experiments, using a high-momentum probe to remove one fast nucleon from the nucleus effectively breaks a pair and releases the second nucleon of the correlation. Brookhaven National Laboratory and Jefferson Lab have conducted such tests on the carbon nucleus with a hadronic and electromagnetic probe, respectively. They measured momentum transfers of greater than 1.5 GeV/c and a missing momentum greater than the Fermi momentum of 250 MeV/c.

Both experiments have shown that recoiling nucleons, with a momentum above the Fermi-sea level in the nucleus, are part of a correlated pair and both observed the same strength of proton–neutron correlations (Piasetzky et al. 2006; Subedi et al. 2008). This confirms that the process is accessing a universal property of nuclei unrelated to the probe. The Jefferson Lab’s experiment also observed the proton–proton pairs and used matched-acceptance detectors to determine the ratio of neutron–proton to proton–proton pairs as nearly 20, as figure 3 shows. Calculations explain the magnitude of this neutron–proton to proton–proton ratio as arising from the short-range tensor part, or nucleon–nucleon spin-dependent part, of the nucleon–nucleon force (Sargsian et al. 2005; Schiavilla et al. 2007; Alvioli et al. 2008).

Isolating the signatures of SRCs opens new avenues for the exploration of nucleon–nucleon interactions at short distances, particularly in addressing the long-standing question of how close nucleons have to approach before the nucleons’ quarks reveal themselves. Nucleon degrees of freedom can no longer be used to describe the system.

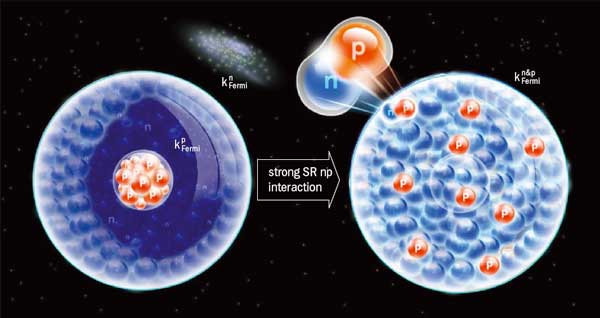
These studies can also influence calculations of the extremely massive. Without SRCs, a large object, such as a neutron star, could be well approximated as a Fermi gas predominantly of neutrons with a small fraction of protons acting as a separate Fermi gas. With SRCs the protons and neutrons interact, strongly enhancing the high-momentum component of the proton momentum distribution, leading to changes in the physical properties of the system (figure 4).

In the future, inclusive short-range-correlation experiments will improve the statistics of the x > 2 data to show definitively whether or not there is indeed a second scaling. These will use targets such as ⁴⁰Ca and ⁴⁸Ca to measure the dependence on the initial-state proton–neutron ratio. The future exclusive experiments will focus on ⁴He (a nucleus where both full and mean-field calculations can come together) and push the limits of the recoil momentum to extend our understanding of the repulsive part of the nucleon–nucleon potential.