Particle physicists and statisticians got together in Durham, UK, last March to discuss statistical techniques of relevance to particle and astroparticle physics analysis. Conference initiator Louis Lyons reports.

Durham University’s Institute for Particle Physics Phenomenology (IPPP) hosted a conference on advanced statistical techniques in particle physics on 18-22 March this year. Building on the success of workshops held at CERN and Fermilab in early 2000 covering the extraction of limits from the non-observation of sought-for signals, the meeting covered a wider range of statistical issues relevant to analysing data and extracting results in particle physics. Astroparticle physics was also included, since many of the analysis problems encountered in this emerging field are similar to those in traditional accelerator experiments.
The IPPP provided an excellent venue for both formal sessions and animated informal discussions, and the only complaint seemed to be that no time was set aside for the participants to visit Durham’s impressive cathedral. Almost 100 physicists attended the conference, joined by two professional statisticians whose presence was invaluable, both in terms of the talks that they gave, and for their incisive comments and advice.
The meeting began with a morning of introductory lectures by Fred James of CERN. Although these lectures were aimed primarily at those who felt the need to be reminded of some statistical principles before the conference proper began, they were attended and enjoyed by most of the participants. James emphasized the five separate statistical activities employed by physicists analysing data: estimating the best value of a parameter; interval estimation; hypothesis testing; goodness of fit; and decision-making. He stressed the importance of knowing which of these activities one is engaged in at any given time.
James also discussed the two different philosophies of statistics – Bayesianism and frequentism. Bayesians are prepared to ascribe a probability distribution to the different possible values of a physical parameter, such as the mass of the muon neutrino. To a frequentist this is anathema, since the mass presumably has a particular value, even if not much is currently known about it. The frequentist would therefore argue that it is meaningless to talk about the probability that it lies in a specified range. Instead, a frequentist would be prepared to use probabilities only for obtaining different experimental results, for any particular value of the parameter of interest. The frequentist restricts himself to the probability of data, given the value of the parameter, while the Bayesian also discusses the probability of parameter values, given the data. Arguments about the relative merits of the two approaches tend to be vigorous.
Michael Goldstein, a statistician from Durham, delivered the first talk of the main conference. On the last day, he also gave his impressions of the meeting. He is a Bayesian, and described particle physics as the last bastion of out-and-out frequentism.
Durham is one of the world’s major centres for the study of parton distributions (describing the way that the momentum of a fast-moving nucleon is shared among its various constituents). Because of this, special attention was given to the statistical problems involved in analysing data to extract these distributions, and to the errors to be assigned to the results. There were talks by Robert Thorne, a phenomenologist from Cambridge, and Mandy Cooper-Sarkar, an Oxford experimentalist working on DESY’s ZEUS experiment. This was followed by a full-day parallel session in which the parton experts continued their detailed discussions. Finally there was an evening gathering over wine and cheese, at which Thorne summarized the various approaches adopted, including the different methods the analyses used for incorporating systematic errors.
Confidence limits
Confidence limits – the subject of the earlier meetings in the series – of course came up again. Alex Read of Oslo University had some beautiful comparisons of the CLs method and the Feldman-Cousins unified technique. CLs is the method used by the LEP experiments at CERN to set exclusion limits on the mass of the postulated Higgs particle that might have been produced at LEP if it had been light enough. The special feature of CLs is that it provides protection against the possibility, arising from a statistical fluctuation of the background, of excluding Higgs masses that are so large that the experiments would be insensitive to them. The main features of the Feldman-Cousins technique are that it reduces the possibility in the standard frequentist approach of ending up with an interval of zero length for the parameter of interest, and it provides a smooth transition between an upper limit on a production rate when the supposed signal is absent or weak, to a two-sided range when it is stronger. Read’s conclusion was that CLs is preferable for exclusion regions, and Feldman-Cousins is better for estimating two-sided intervals.
Staying with limits, Rajendran Raja of Fermilab thought it was important not only to set the magnitude of a limit from a given experiment, but also to give an idea of what the uncertainty in the limit was. Dean Karlen of Ottawa’s Carleton University suggested that as well as specifying the frequentist confidence level at which an interval or limit was calculated, one should also inform the reader of its Bayesian credibility level. This again was an attempt to downplay the emphasis on very small frequentist intervals, which can occur when expected background rates are larger than the observed rate. Another contribution by Carlo Giunti of Turin emphasized that it may be worth using a biased method for obtaining limits, as this could give better power against excluding alternative parameter values.
Discovery significance
Hopefully, not all experiments searching for new effects will obtain null results, and simply set limits. When an effect appears, it is important to assess its significance. This was the subject of a talk by Pekka Sinervo of Toronto, which included several examples from the recent past, such as the discoveries of the top quark and of oscillations in neutral mesons containing bottom quarks.
Several talks dealt with the subject of systematic effects. Roger Barlow of Manchester gave a general review. One particularly tricky subject is how to incorporate systematic effects in the calculation of limits. For example, in an experiment with no expected background and with detection efficiency e, the 95% confidence level upper on the signal rate is 3.0/e, from both frequentist and Bayesian approaches. However, what happens when the efficiency has an uncertainty? From an ideological point of view, it is desirable to use the same type of method (Bayesian or frequentist) both for the incorporation of the systematic and for the evaluation of the limit. Some interesting problems with the Bayesian approach were discussed by Luc Demortier of Rockefeller University, while Giovanni Punzi and Giovanni Signorelli, both of Pisa, spoke about features of the frequentist method, with illustrations from a neutrino oscillations experiment.
The question of how to separate signal from background was another popular topic. It was reviewed by Harrison Prosper of Florida State University, who is active in Fermilab’s Run 2 advanced analysis group, where the topic is actively studied. His talk was complemented by that of Rudy Bock of CERN, who compared the performance of various techniques used for separating cosmic-ray air showers initiated by photons or by hadrons. The relatively new method of support vector machines was described by Tony Vaiciulis of Rochester, while Sherry Towers of Stony Brook made the point that including useless variables could well have the effect of degrading the performance of the signal-to-background separation technique. She also spoke about using kernel methods for turning multidimensional Monte Carlo distributions into probability density estimates. Monte Carlo methods were the subject of two talks by CERN’s Niels Kjaer. With the need for large Monte Carlo samples, it is important to understand how to use the generators efficiently.
In searching for new or rare effects, it is important not to use the data to tune the analysis procedure so as to maximize (or minimize) the sought-for effect. One way of avoiding this is to perform a blind analysis. Paul Harrison of Queen Mary, University of London, described the psychological, sociological and physics issues in using this increasingly popular procedure.
Whatever the method used to extract a parameter from the data, it is important to check whether the data is consistent with the assumed model. When there is enough data, the well known c2 method can be employed, but this is less useful with sparse data, especially in many dimensions. James of CERN and Berkan Aslan of Siegen both spoke about this topic, with the latter showing interesting comparisons of the performance of a variety of methods.
A mundane but very important topic is the understanding of the alignment of the different components of one’s detector. Hamburg’s Volker Blobel explained how this can be done using real tracks in the detector, without the need to invert enormous matrices. In a separate talk, also involving the clever use of matrices, he described his method for unfolding the smearing effects of a detector. This enables one to reconstruct a good approximation to the true distribution from the observed smeared one, without encountering numerical instabilities. Glen Cowan of Royal Holloway, University of London, gave a more general review of deconvolution techniques.
Although textbook statistics can give neat solutions to data analysis problems, real-life situations often involve many complications and require semi-arbitrary decisions. There were several contributions on work at the pit-face. Chris Parkes of Glasgow described how the LEP experiments combined information on W bosons. Their mass is fairly precisely determined, and the well known best linear unbiased estimate (BLUE) method has been used for combining the different results. Nevertheless, problems do arise from different experiments making different assumptions, for example about systematic effects. These difficulties multiply for determining such quantities as triple gauge couplings where the errors are large, where likelihood functions are non-Gaussian and can have more than one maximum, and where the experiments use different analysis procedures. Here again, sociology plays an important role.
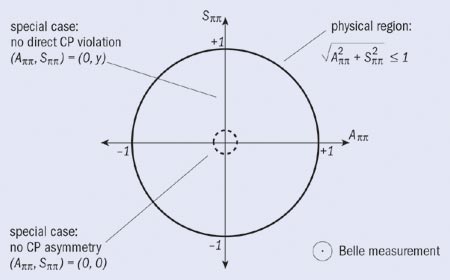
Nigel Smith of the UK Rutherford Appleton Laboratory and Daniel Tovey of Sheffield University presented interesting contributions on dark matter searches. Fabrizio Parodi of Genoa talked about Bs oscillations, and a whole variety of results from the Belle experiment at Japan’s KEK laboratory were also discussed. An interesting point from the last talk, by Bruce Yabsley of Virginia Tech, related to the determination of two parameters (App and Spp) in an analysis of B decays to p+p–, to look for CP violation. Physically the parameters are forced to lie within the unit circle. In the absence of CP violation, they are both zero, while if there is no direct CP violation, App is zero. The Belle estimate (figure 1) lies outside the unit circle. This sounds like a case for taking the physical region into account from first principles (as in Feldman-Cousins), but there are complicated details that make this difficult to implement.
Many discussions started at the conference have continued, and some issues will undoubtedly resurface at the next meeting, scheduled to be held at SLAC in California, US, on 8-12 September 2003.





