Marek Karliner and Jonathan Rosner ask what makes tetraquarks and pentaquarks tick, revealing them to be at times exotic compact states, at times hadronic molecules and at times both – with much still to be discovered.
Breakthroughs are like London buses. You wait a long time, and three turn up at once. In 1963 and 1964, Murray Gell-Mann, André Peterman and George Zweig independently developed the concept of quarks (q) and antiquarks (q) as the fundamental constituents of the observed bestiary of mesons (qq) and baryons (qqq).
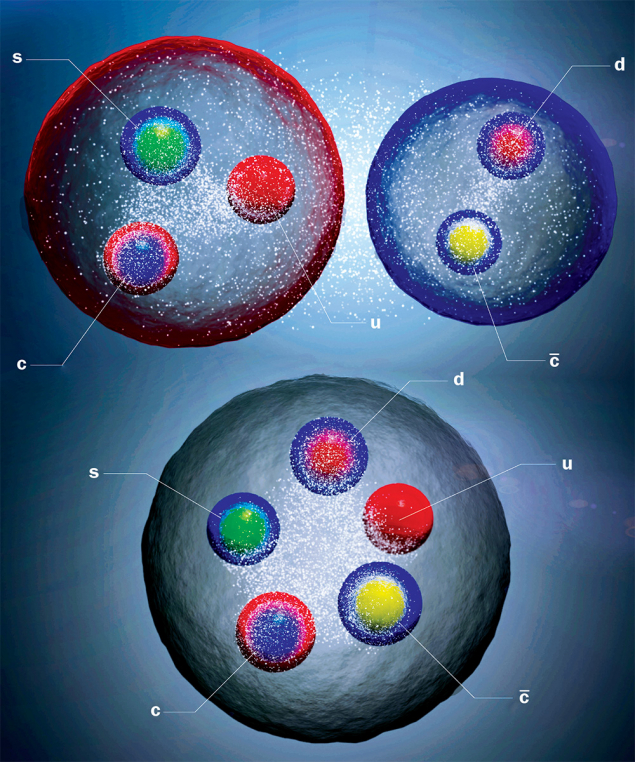
But other states were allowed too. Additional qq pairs could be added at will, to create tetraquarks (qqqq), pentaquarks (qqqqq) and other states besides. In the
1970s, Robert L Jaffe carried out the first explicit calculations of multiquark states, based on the framework of the MIT bag model. Under the auspices of the new theory of quantum chromodynamics (QCD), this computationally simplified model ignored gluon interactions and considered quarks to be free, though confined in a bag with a steep potential at its boundary. These and other early theoretical efforts triggered many experimental searches, but no clear-cut results.
New regimes
Evidence for such states took nearly two decades to emerge. The essential precursors were the discovery of the charm quark (c) at SLAC and BNL in the November Revolution of 1974, some 50 years ago (p41), and the discovery of the bottom quark (b) at Fermilab three years later. The masses and lifetimes of these heavy quarks allowed experiments to probe new regimes in parameter space where otherwise inexplicable bumps in energy spectra could be resolved (see “Heavy breakthroughs” panel).
Heavy breakthroughs
into two pairs of muons (blue and red trajectories) in the CMS detector at CERN. Credit: CMS Collab.
With the benefit of hindsight, it is clear why early experimental efforts did not find irrefutable evidence for multiquark states. For a multiquark state to be clearly identifiable, it is not enough to form a multiquark colour-singlet (a mixture of colourless red–green–blue, red–antired, green–antigreen and blue–antiblue components). Such a state also needs to be narrow and long-lived enough to stand out on top of the experimental background, and has to have distinct decay modes that cannot be explained by the decay of a conventional hadron. Multiquark states containing only light quarks (up, down and strange) typically have many open decay channels, with a large phase space, so they tend to be wide and short-lived. Moreover, they share these decay channels with excited states of conventional hadrons and mix with them, so they are extremely difficult to pin down.
Multiquark states with at least one heavy quark are very different. Once hadrons are “dressed” by gluons, they acquire effective masses of the order of several hundred MeV, with all quarks coupling in the same way to gluons. For light quarks, the bare quark masses are negligible compared to the effective mass, and can be neglected to zeroth order. But for heavy quarks (c or b), the ratio of the bare quark masses to the effective mass of the hadron dramatically affects the dynamics and the experimental situation, creating narrow multiquark states that stand out. These states were not seen in the early searches simply because the relevant production cross sections are very small and particle identification requires very high spatial resolution. These features became accessible only with the advent of the huge luminosity and the superb spatial resolution provided by vertex detectors in bottom and charm factories such as BaBar, Belle, BESIII and LHCb.
The attraction between two heavy quarks scales like α2s mq, where αs is the strong coupling constant and mq is the mass of the quarks. This is because the Coulomb-like part of the QCD potential dominates, scaling as –αs/r as a function of distance r, and yielding an analogue of the Bohr radius ~1/(αsmq). Thus, the interaction grows approximately linearly with the heavy quark mass. In at least one case (discussed below), the highly anticipated but as yet undiscovered bbud. tetraquark Tbb is expected to result in a state with a mass that is below the two-meson threshold, and therefore stable under strong interactions.
Exclusively heavy states are also possible. In 2020 and in 2024, respectively, LHCb and CMS discovered exotic states Tcccc(6900) and Tcccc(6600), which both decay into two J/ψ particles, implying a quark content (cccc). J/ψ does not couple to light quarks, so these states are unlikely to be hadronic molecules bound by light meson exchange. Though they are too heavy to be the ground state of a (cccc) compact tetraquark, they might perhaps be its excitations. Measuring their spin and parity would be very helpful in distinguishing between the various alternatives that have been proposed.
The first unambiguously exotic hadron, the X(3872) (dubbed χc1(3872) in the LHCb collaboration’s new taxonomy; see “What’s in a name?” panel), was discovered at the Belle experiment at KEK in Japan in 2003. Subsequently confirmed by many other experiments, its nature is still controversial. (More of that later.) Since then, there has been a rapidly growing body of experimental evidence for the existence of exotic multiquark hadrons. New states have been discovered at Belle, at the BaBar experiment at SLAC in the US, at the BESIII experiment at IHEP in China, and at the CMS and LHCb experiments at CERN (see “A bestiary of exotic hadrons“). In all cases with robust evidence, the exotic new states contain at least one heavy charm or bottom quark. The majority include two.
The key theoretical question is how the quarks are organised inside these multiquark states. Are they hadronic molecules, with two heavy hadrons bound by the exchange of light mesons? Or are they compact objects with all quarks located within a single confinement volume?
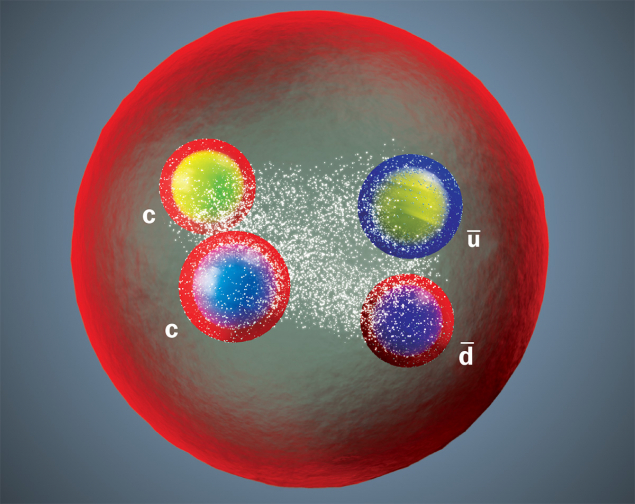
The compact and molecular interpretations each provide a natural explanation for part of the data, but neither explains all. Both kinds of structures appear in nature, and certain states may be superpositions of compact and molecular states.
In the molecular case the deuteron is a good mental image. (As a bound state of a proton and a neutron, it is technically a molecular hexaquark.) In the compact interpretation, the diquark – an entangled pair of quarks with well-defined spin, colour and flavour quantum numbers – may play a crucial role. Diquarks have curious properties, whereby, for example, a strongly correlated red–green pair of quarks can behave like a blue antiquark, opening up intriguing possibilities for the interpretation of qqqq and qqqqq states.
Compact states
A clearcut example of a compact structure is the Tbb tetraquark with quark content bbud. Tbb has not yet been observed experimentally, but its existence is supported by robust theoretical evidence from several complementary approaches. As for any ground-state hadron, its mass is given to a good approximation by the sum of its constituent quark masses and their (negative) binding energy. The constituent masses implied here are effective masses that also include the quarks’ kinetic energies. The binding energy is negative as it was released when the compact state formed.
In the case of Tbb, the binding energy is expected to be so large that its mass is below all two-meson decay channels: it can only decay weakly, and must be stable with respect to the strong interaction. No such exotic hadron has yet been discovered, making Tbb a highly prized target for experimentalists. Such a large binding energy cannot be generated by meson exchange and must be due to colour forces between the very heavy b quarks. Tbb is an isoscalar with JP = 1+. Its charmed analogue, Tcc = (ccud), also known as Tcc(3875)+, was observed by LHCb in 2021 to be a whisker away from stability, with a very small binding energy and width less than 1 MeV (CERN Courier September/October 2021 p7). The big difference between the binding energies of Tbb and Tcc, which make the former stable and the latter unstable, is due to the substantially greater mass of the b quark than the c quark, as discussed in the panel above. An intermediate case, Tbc = (bcud), is very likely also below threshold for strong decay and therefore stable. It is also easier to produce and detect than Tbb and therefore extremely tempting experimentally.
Molecular pentaquarks
At the other extreme, we have states that are most probably pure hadronic molecules. The most conspicuous examples are the Pc(4312), Pc(4440) and Pc(4457) pentaquarks discovered by LHCb in 2019, and labelled according to the convention adopted by the Particle Data Group as Pcc(4312)+, Pcc(4440)+ and Pcc(4457)+. All three have quark content (ccuud) and decay into J/ψp, with an energy release of order 300 MeV. Yet, despite having such a large phase space, all three have anomalously narrow widths less than about 10 MeV. Put more simply, the pentaquarks decay remarkably slowly, given how much energy stands to be released.
But why should long life count against the pentaquarks being tightly bound and compact? In a compact (ccuud) state there is nothing to prevent the charm quark from binding with the anticharm quark, hadronising as J/ψ and leaving behind a (uud) proton. It would decay immediately with a large width.
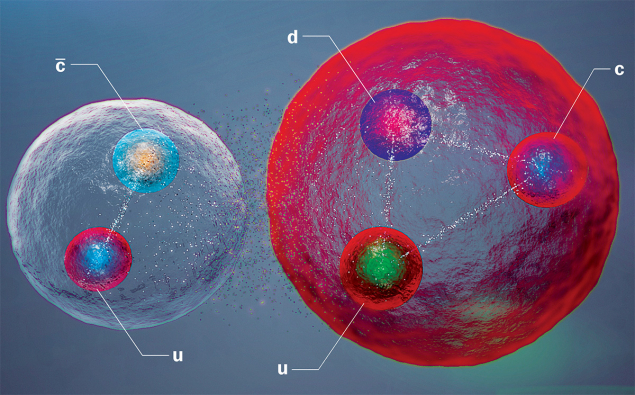
On the other hand, hadronic molecules such as ΣcD and ΣcD* automatically provide a decay-suppression mechanism. Hadronic molecules are typically large, so the c quark inside the Σc baryon is typically far from the c quark inside the D or D* meson. Because of this, the formation of J/ψ = (c c) has a low probability, resulting in a long lifetime and a narrow width. (Unstable particles decay randomly within fixed half-lives. According to Heisenberg’s uncertainty principle, this uncertainty on their lifetime yields a reciprocal uncertainty on their energy, which may be directly observed as the width of the peak in the spectrum of their measured masses when they are created in particle collisions. Long-lived particles exhibit sharply spiked peaks, and short-lived particles exhibit broad peaks. Though the lifetimes of strongly interacting particle are usually not measurable directly, they may be inferred from these “widths”, which are measured in units of energy.)
Additional evidence in favour of their molecular nature comes from the mass of Pc(4312) being just below the ΣcD production threshold, and the masses of Pc(4440) and Pc(4457) being just below the ΣcD* production threshold. This is perfectly natural. Hadronic molecules are weakly bound, so they typically only form an S-wave bound state, with no orbital angular momentum. So ΣcD, which combines a spin-1/2 baryon and a spin-0 negative-parity meson, can only form a single state with JP = 1/2–. By contrast, ΣcD*, which combines a spin-1/2 baryon and spin-1 negative-parity meson, can form two closely-spaced states with JP = 1/2– and 3/2–, with a small splitting coming from a spin–spin interaction.
An example of a possible mixture of a compact state and a hadronic molecule is provided by the X(3872) meson
The robust prediction of the JP quantum numbers makes it very straightforward in principle to kill this physical picture, if one were to measure JP values different from these. Conversely, measuring the predicted values of JP would provide a strong confirmation (see “The 23 exotic hadrons discovered at the LHC table”).
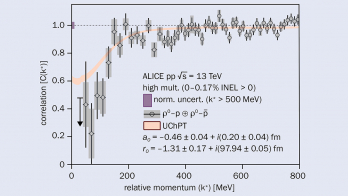
These predictions have already received substantial indirect support from the strange-pentaquark sector. The spin-parity of the Pccs(4338), which also has a narrow width below 10 MeV, has been determined by LHCb to be 1/2–, exactly as expected for a Ξc D molecule (see “Strange pentaquark” figure).
The mysterious X(3872)
An example of a possible mixture of a compact state and a hadronic molecule is provided by the already mentioned X(3872) meson. Its mass is so close to the sum of the masses of a D0 meson and a D*0 meson that no difference has yet been established with statistical significance, but it is known to be less than about 1 MeV. It can decay to J/ψπ+π– with a branching ratio (3.5 ± 0.9)%, releasing almost 500 MeV of energy. Yet its width is only of order 1 MeV. This is an even more striking case of relative stability in the face of naively expected instability than for the pentaquarks. At first sight, then, it is tempting to identify X(3872) as a clearcut D0D*0 hadronic molecule.

The situation is not that simple, however. If X(3872) is just a weakly-bound hadronic molecule, it is expected to be very large, of the scale of a few fermi (10–15 m). So it should be very difficult to produce it in hard reactions, requiring a large momentum transfer. Yet this is not the case. A possible resolution might come from X(3872) being a mixture of a D0D*0molecular state and χc1(2P), a conventional radial excitation of P-wave charmonium, which is much more compact and is expected to have a similar mass and the same JPC = 1++ quantum numbers. Additional evidence in favour of such a mixing comes from comparing the rates of the radiative decays X(3872) → J/ψγ and X(3872) → ψ(2S)γ.
The question associated with exotic mesons and baryons can be posed crisply: is an observed state a molecule, a compact multiquark system or something in between? We have given examples of each. Definitive compact-multiquark behaviour can be confirmed if a state’s flavour-SU(3) partners are identified. This is because compact states are bound by colour forces, which are only weakly sensitive to flavour-SU(3) rotations. (Such rotations exchange up, down and strange quarks, and to a good approximation the strong force treats these light flavours equally at the energies of charmed and beautiful exotic hadrons.) For example, if X(3872) should in fact prove to be a compact tetraquark, it should have charged isospin partners that have not yet been observed.
On the experimental front, the sensitivity of LHCb, Belle II, BESIII, CMS and ATLAS have continued to reap great benefits to hadron spectroscopy. Together with the proposed super τ-charm factory in China, they are virtually guaranteed to discover additional exotic hadrons, expanding our understanding of QCD in its strongly interacting regime.
Further reading
M Karliner et al. 2018 Ann. Rev. Nucl. Part. Sci. 68 17–44.
S L Olsen et al. 2018 Rev. Mod. Phys. 90 015003.
A Esposito et al. 2017 Phys. Rept. 668 1–97.
F K Guo et al. 2018 Rev. Mod. Phys. 90 015004.
N Brambilla et al. 2021 arXiv:2203.16583.