Geared for discovery more so than delicacy, the LHC is defying expectations by rivalling lepton colliders for precision. Guillelmo Gomez-Ceballos and Jan Kretzschmar identify five measurements of the electroweak interaction where the LHC experiments are pushing the boundaries of our knowledge.

The Standard Model – an inconspicuous name for one of the great human inventions. It describes all known elementary particles and their interactions, except for gravity. About 19 free parameters tune its behaviour. To the best of our knowledge, they could in principle take any value, and no underlying theory yet conceived can predict their values. They include particle masses, interaction strengths, important technical numbers such as mixing angles and phases, and the vacuum strength of the Higgs field, which theorists believe has alone among fundamental fields permeated every cubic attometre of the universe, since almost the beginning of time. Measuring these parameters is the most fundamental experimental task available to modern science.
The basic constituents of matter interact through forces which are mediated by virtual particles that ping back and forth, delivering momentum and quantum numbers. The gluon mediates the strong interaction, the photon mediates the electromagnetic interaction, and the W and Z bosons mediate the weak interaction. Although the electromagnetic and weak forces operate very differently to each other in everyday life, in the Standard Model they are two manifestations of the broken electroweak interaction – an interaction that broke when the Higgs field switched on throughout the universe, giving mass to matter particles, the W and Z bosons, and the Higgs boson itself, via the Brout–Englert–Higgs (BEH) mechanism. The electroweak theory has been extraordinarily successful in describing experimental results, but it remains mysterious – and the BEH mechanism is the origin of some of those free parameters. The best way to test the electroweak model is to over-constrain its free parameters using precision measurements and try to find a breaking point.

Ever since the late 1960s, when Steven Weinberg, Sheldon Glashow and Abdus Salam unified the electromagnetic and weak forces using the BEH mechanism, CERN has had an intimate experimental relationship with the electroweak theory. In 1973 the Z boson was indirectly discovered by observing “neutral current” events in the Gargamelle bubble chamber, using a neutrino beam from the Proton Synchrotron. The W boson was discovered in 1983 at the Super Proton Synchrotron collider, followed by the direct observation of the Z boson in the same machine soon after. The 1990s witnessed a decade of exquisite electroweak precision measurements at the Large Electron Positron (LEP) collider at CERN and the Stanford Linear Collider (SLC) at SLAC National Accelerator Laboratory in the US, before the crown jewel of the electroweak sector, the Higgs boson, was discovered by the ATLAS and CMS collaborations at the Large Hadron Collider (LHC) in 2012 – a remarkable success that delivered the last to be observed, and arguably most mysterious, missing piece of the Standard Model.
What was not expected, was that the ATLAS, CMS and LHCb experiments at the LHC would go on to make electroweak measurements that rival in precision those made at lepton colliders.
Discovery or precision?
Studying the electroweak interaction requires a supply of W and Z bosons. For that, you need a collider. Electrons and positrons are ideally suited for the task as they interact exclusively via the electroweak interaction. By precisely tuning the energy of electron–positron collisions, experiments at LEP and the SLC tested the electroweak sector with an unprecedented 0.1% accuracy at the energy scale of the Z-boson mass (mZ).

Hadron colliders like the LHC have different strengths and weaknesses. Equipped to copiously produce all known Standard Model particles – and perhaps also hypothetical new ones – they are the ultimate instruments for probing the high-energy frontier of our understanding of the microscopic world. The protons they collide are not elementary, but a haze of constituent quarks and gluons that bubble and fizz with quantum fluctuations. Each constituent “parton” carries an unpredictable fraction of the proton’s energy. This injects unavoidable uncertainty into studies of hadron collisions that physicists attempt to encode in probabilistic parton distribution functions. What’s more, when a pair of partons from the two opposing protons interact in an interesting way, the result is overlaid by numerous background particles originating from the remaining partons that were untouched by the original collision – a complexity that is exacerbated by the difficult-to-model strong force which governs the behaviour of quarks and gluons. As a result, hadron colliders have a reputation for being discovery machines with limited precision.

The LHC has collided protons at the energy frontier since 2010, delivering far more collisions than comparable previous machines such as the Tevatron at Fermilab in the US. This has enabled a comprehensive search and measurement programme. Following the discovery of the Higgs boson in 2012, measurements have so far verified its place in the electroweak sector of the Standard Model, although the relative precisions of many measurements are currently far lower than those achieved for the W and Z bosons at LEP. But in defiance of expectations, the capabilities of the LHC experiments and the ingenuity of analysts have also enabled many of the world’s most precise measurements of the electroweak interaction. Here, we highlight five.
1. Producing W and Z bosons
When two streams of objects meet, how many strike each other depends on their cross-sectional area. Though quarks and other partons are thought to be fundamental objects with zero extent, particle physicists borrow this logic for particle beams, and extend it by subdividing the metaphorical cross section according to the resulting interactions. The range of processes used to study W and Z bosons at the LHC spans a remarkable eight orders of magnitude in cross section.
The most common interaction is the production of single W and Z bosons through the annihilation of a quark and an antiquark in the colliding protons. Measurements with single W and Z boson events have now reached a precision well below 1% thanks to the excellent calibration of the detector performance. They are a prodigious tool for testing and improving the modelling of the underlying process, for example using parton distribution functions.
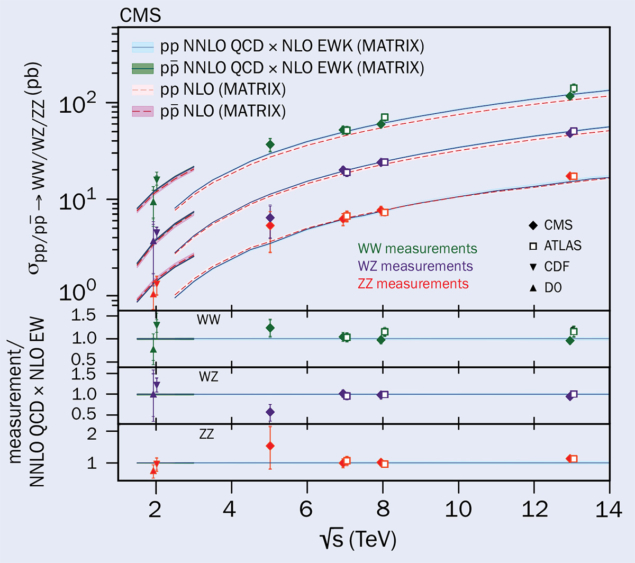
The second most common interaction is the simultaneous production of two bosons. Measurements of “diboson” processes now routinely reach a precision better than 5%. Since the start of the LHC operation, the accelerator has operated at several collision energies, allowing the experiments to map diboson cross sections as a function of energy. Measurements of the cross sections for creating WW, WZ and ZZ pairs exhibit remarkable agreement with state-of-the art Standard Model predictions (see “Diboson production” figure).
The large amount of collected data at the LHC has recently allowed us to move the frontier to the observation of extremely infrequent “triboson” processes with three W or Z bosons, or photons, produced simultaneously – the first step towards confirming the existence of the quartic self-interaction between the electroweak bosons.
2. The weak mixing angle
The Higgs potential is famously thought to resemble a Mexican hat. The Higgs field that permeates space could in principle exist with a strength corresponding to any point on its surface. Theorists believe it settled somewhere in the brim a picosecond or so after the Big Bang, breaking the perfect symmetry of the hat’s apex, where its value was zero. This switched the Higgs field on throughout the universe – and the massless gauge bosons of the unified electroweak theory mixed to form the photon and W and Z boson mass eigenstates that mediate the broken electroweak interaction today. The weak mixing angle θW is the free parameter of the Standard Model which defines that mixing.

The θW angle can be studied using a beautifully simple interaction: the annihilation of a quark and its antiquark to create an electron and a positron or a muon and an antimuon. When the pair has an invariant mass in the vicinity of mZ, there is a small preference for the negatively charged lepton to be produced in the same direction as the initial quark. This arises due to quantum interference between the Z boson’s vector and axial-vector couplings, whose relative strengths depend on θW.
The unique challenge at a proton–proton collider like the LHC is that the initial directions of the quark and the antiquark can only be inferred using our limited knowledge of parton distribution functions. These systematic uncertainties currently dominate the total uncertainty, although they can be reduced somewhat by using information on lepton pairs produced away from the Z resonance. The CMS and LHCb collaborations have recently released new measurements consistent with the Standard Model prediction with a precision comparable to that of the LEP and SLC experiments (see “Weak mixing angle” figure).
Quantum physics effects play an interesting role here. In practice, it is not possible to experimentally isolate “tree level” properties like θW, which describe the simplest interactions that can be drawn on a Feynman diagram. Measurements are in fact sensitive to the effective weak mixing angle, which includes the effect of quantum interference from higher-order diagrams.
A crucial prediction of electroweak theory is that the masses of the W and Z bosons are, at leading order, related by the electroweak mixing angle: sin2θW = 1–m2W/m2Z, where mW and mZ are the masses of the W and Z bosons. This relationship is modified by quantum loops involving the Higgs boson, the top quark and possibly new particles. Measuring the parameters of the electroweak theory precisely, therefore, allows us to test for any gaps in our understanding of nature.
Surprisingly, combining this relationship with the mZ measurement from LEP and the CMS measurement of θW also allows a competitive measurement of mW. A measurement of sin2θW with a precision of 0.0003 translates into a prediction of mW with 15 MeV precision, which is comparable to the best direct measurements.
3. The mass and width of the W boson
Precisely measuring the mass of the W boson is of paramount importance to efforts to further constrain the relationships between the parameters of the electroweak theory, and probe possible beyond-the-Standard Model contributions. Particle lifetimes also offer a sensitive test of the electroweak theory. Because of their large masses and numerous decay channels, the W and Z bosons have mean lifetimes of less than 10–24 s. Though this is an impossibly brief time interval to measure directly, Heisenberg’s uncertainty principle smudges a particle’s observed mass by a certain “width” when it is produced in a collider. This width can be measured by fitting the mass distribution of many virtual particles. It is reciprocally related to the particle’s lifetime.
While lepton-collider measurements of the properties of the Z boson were extensive and achieved remarkable precision, the same is not quite true for the W boson. The mass of the Z boson was measured with a precision of 0.002%, but the mass of the W boson was measured with a precision of only 0.04% – a factor 20 worse. The reason is that while single Z bosons were copiously produced at LEP and SLC, W bosons could not be produced singly, due to charge conservation. W+W– pairs were produced, though only at low rates at LEP energies.
In contrast to LEP, hadron colliders produce large quantities of single W bosons through quark–antiquark annihilation. The LHC produces more single W bosons in a minute than all the W-boson pairs produced in the entire lifetime of LEP. Even when only considering decays to electrons or muons and their respective neutrinos – the most precise measurements – the LHC experiments have recorded billions of W-boson events.
But there are obstacles to overcome. The neutrino in the final state escapes undetected. Its transverse momentum with respect to the beam direction can only be measured indirectly, by measuring all other products of the collision – a major experimental challenge in an environment with not just one, but up to 60 simultaneous proton–proton collisions. Its longitudinal momentum cannot be measured at all. And as the W bosons are not produced at rest, extensive theoretical calculations and ancillary measurements are needed to model their momenta, incurring uncertainties from parton distribution functions.
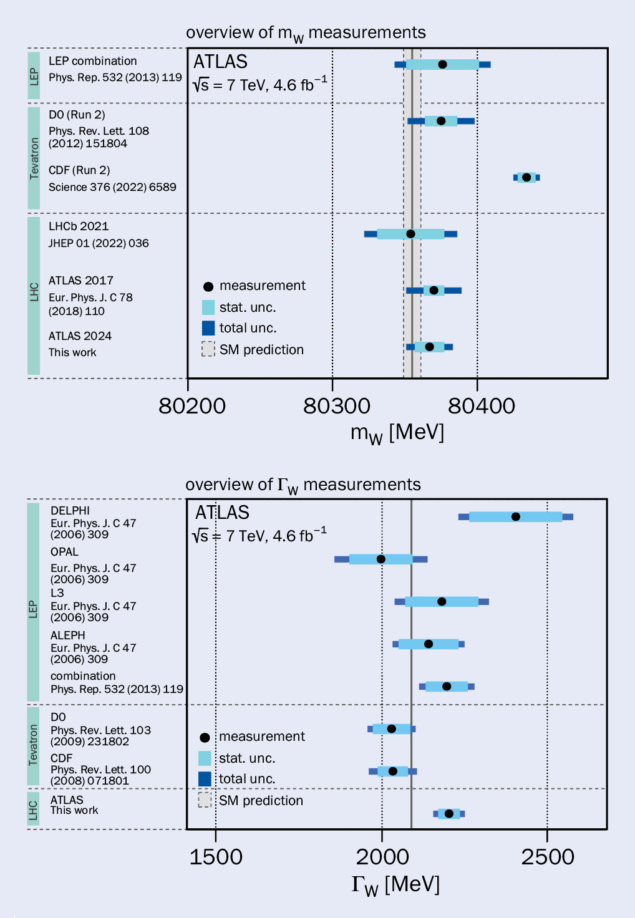
Despite these challenges, the latest measurement of the W boson’s mass by the ATLAS collaboration achieved a precision of roughly 0.02% (see “Mass and width” figure, top). The LHCb collaboration also recently produced its first measurement of the W-boson mass using W bosons produced close to the beam line with a precision at the 0.04% level, dominated for now by the size of the data sample. Owing to the complementary detector coverage of the LHCb experiment with respect to the ATLAS and CMS experiments, several uncertainties are reduced when these measurements are combined.
The Tevatron experiments CDF and D0 also made precise W-boson measurements using proton–antiproton collisions at a lower centre-of-mass energy. The single most precise mass measurement, at the 0.01% level, comes from CDF. It is in stark disagreement with the Standard Model prediction and disagrees with the combination of other measurements.
A highly anticipated measurement by the CMS collaboration may soon weigh in decisively in favour either of the CDF measurement or the Standard Model. The CMS measurement will combine innovative analysis techniques using the Z boson with a larger 13 TeV data set than the 7 TeV data used by the recent ATLAS measurement, enabling more powerful validation samples and thereby greater power to reduce systematic uncertainties.
Measurements of the W boson’s width are not yet sufficiently precise to constrain the Standard Model significantly, though the strongest constraint so far comes from the ATLAS collaboration (see “Mass and width” figure, bottom). Further measurements are a promising avenue to test the Standard Model. If the W boson decays into any hitherto undiscovered particles, its lifetime should be shorter than predicted, and its width greater, potentially indicating the presence of new physics.
4. Couplings of the W boson to leptons
Within the Standard Model, the W and Z bosons have equal couplings to leptons of each of the three generations – a property known as lepton flavour universality (LFU). Any experimental deviation from LFU would indicate new physics.
As with mass and width, lepton colliders’ precision was superior for the Z boson than the W boson. LEP confirmed LFU in leptonic Z-boson decays to about 0.3%. Comparing the three branching fractions of the W boson in the electron, muon and tau–lepton decay channels, the combination of the four LEP experiments reached a precision of only about 2%.
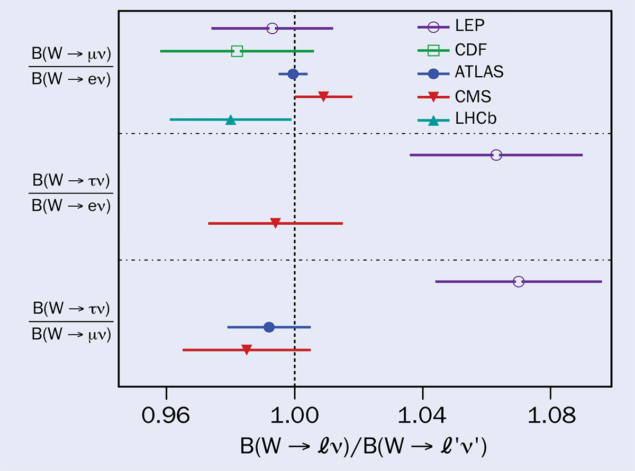
At the LHC, the large cross section for producing top quark–antiquark pairs that both decay into a W boson and a bottom quark offers a unique sample of W-boson pairs for high-precision studies of their decays. The resulting measurements are the most precise tests of LFU for all three possible comparisons of the coupling of the lepton flavours to the W boson (see “Couplings to leptons” figure).
Regarding the tau lepton to muon ratio, the ATLAS collaboration observed 0.992 ± 0.013 decays to a tau for every one decay to a muon. This result favours LFU and is twice as precise than the corresponding LEP result of 1.066 ± 0.025, which exhibits a deviation of 2.6 standard deviations from unity. Because of the relatively long tau lifetime, ATLAS was able to separate muons produced in the decay of tau leptons from those produced promptly by observing the tau decay length of the order of 2 mm.
The best tau to electron measurement is provided by a simultaneous CMS measurement of all the leptonic and hadronic decay branching fractions of the W boson. The analysis splits the top quark–antiquark pair events based on the multiplicity and flavour of reconstructed leptons, the number of jets, and the number of jets identified as originating from the hadronisation of b quarks. All CMS ratios are consistent with the LFU hypothesis and reduce tension with the Standard Model prediction.
Regarding the muon to electron ratio, measurements have been performed by several LHC and Tevatron experiments. The observed results are consistent with LFU, with the most precise measurement from the ATLAS experiment boasting a precision better than 0.5%.
5. The invisible width of the Z boson
A groundbreaking measurement at LEP deduced how often a particle that cannot be directly observed decays to particles that cannot be detected. The particle in question is the Z boson. By scanning the energy of electron–positron collisions and measuring the broadness of the “lineshape” of the smudged bump in interactions around the mass of the Z, LEP physicists precisely measured its width. As previously noted, a particle’s width is reciprocal to its lifetime and therefore proportional to its decay rate – something that can also be measured by directly accounting for the observed rate of decays to visible particles of all types. The difference between the two numbers is due to Z-boson decays to so-called invisible particles that cannot be reconstructed in the detector. A seminal measurement concluded that exactly three species of light neutrino couple to the Z boson.
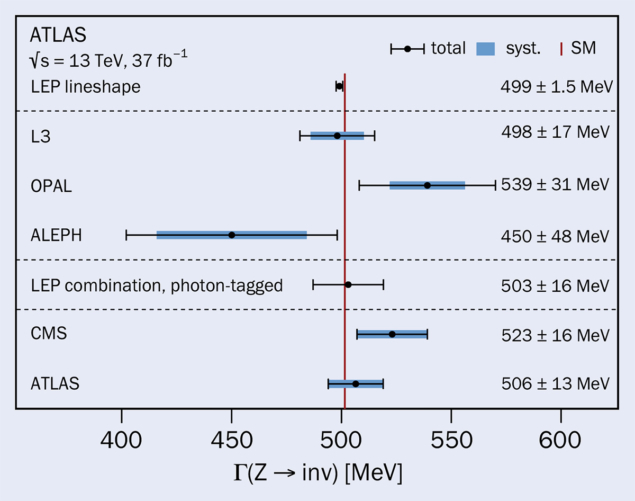
The LEP experiments also measured the invisible width of the Z boson using an ingenious method that searched for solitary “recoils”. Here, the trick was to look for the rare occasion when the colliding electron or positron emitted a photon just before creating a virtual Z boson that decayed invisibly. Such events would yield nothing more than a single photon recoiling from an otherwise invisible Z-boson decay.
The ATLAS and CMS collaborations recently performed similar measurements, requiring the invisibly decaying Z boson to be produced alongside a highly energetic jet in place of a recoil photon. By taking the ratio with equivalent recoil decays to electrons and muons, they achieved remarkable uncertainties of around 2%, equivalent to LEP, despite the much more challenging environment (see “Invisible width” figure). The results are consistent with the Standard Model’s three generations of light neutrinos.
Future outlook
Building on these achievements, the LHC experiments are now readying themselves for a more than comparable experimental programme, which is yet to begin. Following the ongoing run of the LHC, a high-luminosity upgrade (HL-LHC) is scheduled to operate throughout the 2030s, delivering a total integrated luminosity of 3 ab–1 to both ATLAS and CMS. The LHCb experiment also foresees a major upgrade to collect an integrated luminosity of more than 300 fb–1 by the end of the LHC operations. A tenfold data set, upgraded detectors and experimental methods, and improvements to theoretical modelling will greatly extend both experimental precision and the reach of direct and indirect searches for new physics. Unprecedented energy scales will be probed and anomalies with respect to the Standard Model may become apparent.

Despite the significant challenges posed by systematic uncertainties, there are good prospects to further improve uncertainties in precision electroweak observables such as the mass of the W boson and the effective weak mixing angle, thanks to the larger angular acceptances of the new inner tracking devices currently under production by ATLAS and CMS. A possible programme of high-precision measurements in electron–proton collisions, the LHeC, could deliver crucial input to reduce uncertainties such as from parton distribution functions. The LHeC has been proposed to run concurrently with the HL-LHC by adding an electron beam to the LHC.
Beyond the HL-LHC programme, several proposals for future particle colliders have captured the imagination of the global particle-physics community – and not least the two phases of the Future Circular Collider (FCC) being studied at CERN. With a circumference three to four times greater than that of the LEP/LHC tunnel, electron–positron collisions could be delivered with very high luminosity and centre-of-mass energies from 90 to 365 GeV in the initial FCC-ee phase. The FCC-ee would facilitate an impressive leap in the precision of most electroweak observables. Projections estimate a factor of 10 improvement for Z-boson measurements and up to 100 for W-boson measurements. For the first time, the top quark could be produced in an environment where it is not colour-connected to initial hadrons, in some cases reducing uncertainties by a factor of 10 or more.
The LHC collaborations have made remarkable strides forward in probing the electroweak theory – a theory of great beauty and consequence for the universe. But its most fundamental workings are subtle and elusive. Our exploration is only just beginning.