New results suggest that types of neutrinos that were once thought to be distinct could mix. Here Louis Lyons compares this apparently mysterious mechanism to the behaviour of two simple pendula tied together.
Physicists used to believe that the three types of neutrinos electrons, muons and taus were distinct. Then came the claim that neutrinos could “oscillate” one type can change into another, and then back again and that, as a consequence, at least one type has a non-zero mass.
Cosmic rays hitting the Earth’s atmosphere produce secondary particles, and the new claim was based on observations of the effects of neutrinos produced by cosmic rays. Measured using large underground detectors to record neutrino interactions, the ratio of muon-neutrinos to electron-neutrinos is less than expected.
This is interpreted as being the result of muon-neutrinos changing into a different neutrino type between their production high in the atmosphere and their detection underground. A similar effect is used to explain the fact, known for some 30 years, that the number of neutrinos from the Sun detected on Earth is also smaller than expected from the known solar power output. A third experiment that may have seen oscillation effects was performed at Los Alamos, where some muon-neutrinos produced by an accelerator beam appeared to behave like electron-neutrinos by the time they interacted several metres away.
Oscillations depend on the difference in the mass squared of the two types of neutrinos involved in the oscillation, D(m2), and a mixing parameter. The physical significance of both of these parameters can be understood in terms of a simple analogy with coupled pendula. With two independent pendula of different lengths, the shorter one swings faster than the longer. The situation changes if the two pendula are joined together, for example by an elastic band, when the elasticity of the band governs the coupling between the pendula. This coupling is usually expressed as a “mixing angle”. If the angle is zero, there is no coupling.
For the coupled case, there are special “normal modes” in which the two pendula swing at the same frequency and with constant amplitude. For this to happen, the ratio of the amplitudes must be just right. In fact there are two such modes. In the lower-frequency mode, the pendula swing in phase (if one pendulum is on the left of its equilibrium position at any time, then so is the other), with the longer one having the larger displacement. For the other mode they are out of phase (one swinging to the left when the other goes to the right) and the shorter pendulum has the larger displacement.
Stronger coupling
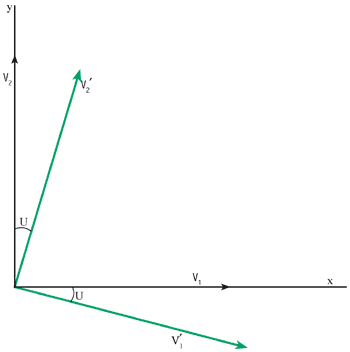
The relative amplitudes of the pendula in these two normal modes are displayed by the vectors v¢2 and v¢1 in figure 1. x is the amplitude of the shorter pendulum and y is the amplitude of the longer one. For given lengths, as the coupling between the pendula becomes stronger, the two vectors rotate together until the mixing angle, q, eventually reaches 45°. As the coupling becomes progressively weaker and q tends to zero, the normal modes correspond to either the shorter pendulum swinging and the longer one being stationary or vice versa.
If we displace just the first pendulum and release it (while the second is in its equilibrium position), it starts swinging with a given amplitude A. However, because of the coupling, its amplitude gradually decreases while that of the second increases. The transfer of energy between the pendula is a beat phenomenon, the frequency of which is just the difference in frequencies of the normal modes of the system. For pendula of unequal length, the transfer of energy is not complete. The amplitude of the first pendulum goes down not to zero, but only to Acos2q, where q is the rotation angle of figure 1, while that of the second reaches Asin2q.
Beat frequency
Now for the neutrino analogy. The first pendulum corresponds to, say, the electron-neutrinos as produced in the Sun, while that of the second pendulum could correspond to the muon-neutrino. As the electron-neutrinos travel towards the Earth, the natural states for describing the way in which they propagate correspond to the normal modes of the coupled pendula. These are “rotated” by the angle q with respect to the electron- and muon-neutrinos (figure 1).
The net effect is that the amplitude for the electron-neutrino changes with time, much as in, with the result that, when they reach the Earth, it is reduced by a factor of as much as cos2q. Meanwhile the muon neutrino component, which was initially absent, has grown by up to sin2q times the initial electron-neutrino amplitude. Therefore, by the time the solar electron-neutrinos are detected on Earth, their flux is smaller than would be expected simply from the rate of electron-neutrino production in the Sun. The exact flux of electron-neutrinos arriving at the Earth will depend on the time it takes for the neutrinos to arrive, expressed as a fraction of the oscillation period. It also depends on cos2q.
The possible oscillation of one type of neutrino into another is thus completely analogous to the beat-type phenomenon of the transfer of energy between two coupled pendula. q is the angle between the neutrino quantum states that participate in the weak interaction (electron- and muon-neutrinos), and the neutrino states that propagate through space. It also appears in the factor cos2q, which is relevant for the minimum amplitude of the electron-neutrino component as it oscillates backward and forwards into the muon-neutrino.
The beat frequency of the actual oscillations depends on the difference in frequencies of the two neutrino states as they propagate through free space. Because neutrinos are highly relativistic, it turns out that this depends on the difference of the squares of their masses. If both neutrinos are massless, there will be no oscillations. (In the coupled pendula example, if the normal mode frequencies were the same there would be no beats.)
Thus the parameters describing the neutrino oscillations have direct analogies to the case of the two coupled pendula. The coupled pendulum problem provides a useful insight into the mysterious world of neutrinos.







