A safe approach to quantum gravity

The LHC experiments at CERN have been extremely successful in verifying the Standard Model (SM) of particle physics to very high precision. From the theoretical perspective, however, this model has two conceptual shortcomings. One is that the SM appears to be an “effective field theory” that is valid up to a certain energy scale only; the other is that gravity is not part of the model. This raises the question of what a theory comprising particle physics and gravity that is valid for all energy scales might look like. This directly leads to the domain of quantum gravity.

The typical scale associated with quantum-gravity effects is the Planck scale: 10¹⁵ TeV, or 10^–35 m. This exceeds the scales accessible at the LHC by approximately 14 orders of magnitude, forcing us to ask: what can theorists possibly gain from investigating physics at energies beyond the Planck scale? The answer is simple: the SM includes many free parameters that must be fixed by experimental data. Since the number of these parameters proliferates when higher order interactions are included, one would like to constrain this high-dimensional parameter space.

At low energies, this can be done by implementing bounds derived from demanding unitarity and causality of physical processes. Ideally, one would like to derive similar constraints from consistency at trans-Planckian scales where quantum-gravity effects may play a major role. At first sight, this may seem counterintuitive. It is certainly true that gravity treated as an effective field theory itself does not yield any effect measurable at LHC scales due to its weakness; the additional constraints then arise from requiring that the effective field theories underlying the SM and gravity can be combined and extended into a framework that is valid at all energy scales. Presumably, this will not work for all effective field theories. Taking a “bottom-up” approach (identifying the set of theories for which this extension is possible) may constrain the set of free parameters. Conversely, to be phenomenologically viable, any theory describing trans-Planckian physics must be compatible with existing knowledge at the scales probed by collider experiments. This “top-down” approach may then constrain the potential physics scenarios happening at the quantum-gravity scale – a trajectory that has been followed, for example, by the swampland programme initiated from string theory at all scales.

From the theoretical viewpoint, the SM is formulated in the language of relativistic quantum field theories. On this basis, it is possible that the top-down route becomes more realistic the closer the formulation of trans-Planckian physics sticks to this language. For example, string theory is a promising candidate for a consistent description of trans-Planckian physics. However, connecting the theory to the SM has proven to be very difficult, mainly due to the strong symmetry requirements underlying the formulation. In this regard, the “asymptotic safety” approach towards quantum gravity may offer a more tractable option for implementing the top-down idea since it uses the language of relativistic quantum field theory.

Asymptotic safety

What is the asymptotic-safety scenario, and how does it link quantum gravity to particle physics? Starting from the gravity side, we have a successful classical theory: Einstein’s general relativity. If one tries to upgrade this to a quantum theory, things go wrong very quickly. In the early 1970s, it was shown by Gerard ’t Hooft and Martinus Veltman that applying the perturbative quantisation techniques that have proved highly successful for particle-physics theories fail for general relativity. In short, it introduces an infinite number of parameters (one for each allowed local interaction) and thus requires an infinite number of independent measurements to determine what the values of those parameters are. Although this path leads us to a quantum theory of gravity valid at all scales, the construction lacks predictive power. Still, it results in a perfectly predictive effective field theory describing gravity up to the Planck scale.

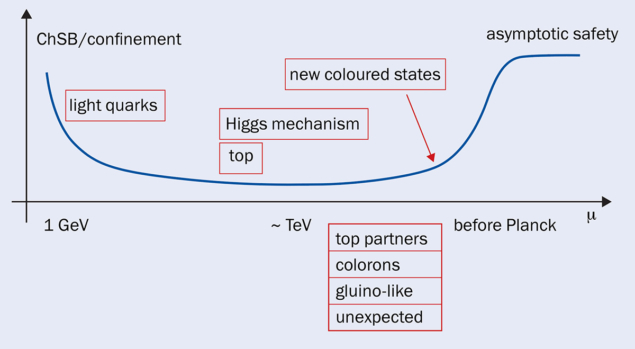
This may seem discouraging when attempting to formulate a quantum field theory of gravity without introducing new symmetry principles, for example supersymmetry, to remove additional free parameters. A loophole is provided by Kenneth Wilson’s modern understanding of renormalisation. Here, the basic idea is to organise quantum fluctuations according to their momentum and integrate-out these fluctuations, starting from the most energetic ones and proceeding towards lower energy modes. This creates what is called the Wilsonian renormalisation-group “flow” of a theory. Healthy high-energy completions are provided by renormalisation-group fixed points. At these special points the theory becomes scale-invariant, which ensures the absence of divergences. The fixed point also provides predictive power via the condition that the renormalisation-group flow hits the fixed point at high energies (see “Safety belt” figure). For asymptotically-free theories, where all interactions switch off at high energies, the underlying renormalisation-group fixed point is the free theory. This can be seen in the example of quantum chromodynamics (QCD): if the QCD gauge coupling diminishes when going to higher and higher energies, it approaches a fixed point at arbitrary high energies that is non-interacting. One can also envision high-energy completions based on a renormalisation-group fixed point with non-vanishing interactions, which is commonly referred to as asymptotic safety.

Forces of nature

In the context of gravity, the asymptotic-safety scenario was first proposed by Steven Weinberg in the late 1970s. Starting with the seminal work by Martin Reuter (University of Mainz) in 1998, the existence of a renormalisation-group fixed point suitable for rendering gravity asymptotically safe – the so-called Reuter fixed point – is supported by a wealth of first-principle computations. While similar constructions are well known in condensed-matter physics, the Reuter fixed point is distinguished by the fact that it may provide a unified description of all forces of nature. As such, it may have profound consequences for our understanding of the physics inside a black hole, give predictions for parameters of the SM such as the Higgs-boson mass, or disfavour certain types of physics beyond the SM.

The asymptotic-safety approach towards quantum gravity may offer a more tractable option for implementing the top-down idea

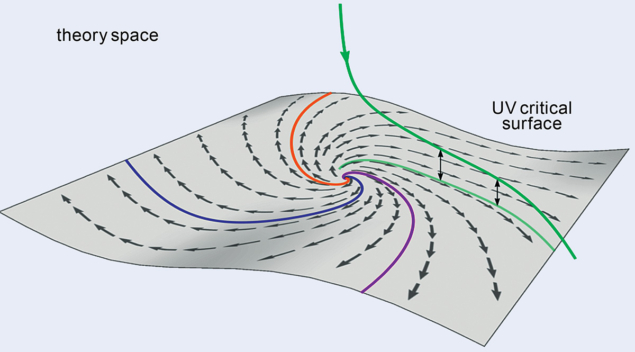
The predictive power of the fixed point arises as follows. Only a finite set of parameters exist that describe consistent quantum field theories emanating from the fixed point. One then starts to systematically integrate-out quantum fluctuations (from high to low energy), resulting in a family of effective descriptions in which the quantum fluctuations are taken into account. In practice, this process is implemented by the running of the theory’s couplings, generating what are known as renormalisation-group trajectories. To be phenomenologically viable, the endpoint of the renormalisation group trajectory must be compatible with observations. In the end, only one (or potentially none) of the trajectories emanating from the fixed point will provide a description of nature (see “Going with the flow” image). According to the asymptotic-safety principle, this trajectory must be identified by fixing the free parameters left by the fixed point based on experiments. Once this process is completed, the construction fixes all couplings in the effective field theory in terms of a few free parameters. Since this entails an infinite number of relations that can be probed experimentally, the construction is falsifiable.

Particle physics link

The link to particle physics follows from the observation that the asymptotic-safety construction remains operative once gravity is supplemented by the matter fields of the SM. Non-abelian gauge groups – such as those underlying the electroweak and strong forces, Yukawa interactions and fermion masses – are readily accommodated. A wide range of proof-of-concepts show that this is feasible, gradually bringing the ultimate computation involving the full SM into reach. The fact that gravity remains interacting at the smallest length scales too implies that the construction will feature non-minimal couplings between matter and the gravitational field as well as matter self-interactions of a very specific type. The asymptotic-safety mechanism may then provide the foundation for a realistic quantum field theory unifying all fundamental forces of nature.

Can particle physics tell us whether this specific idea about quantum gravity is on the right track? After all there still exists the vast hierarchy between the energy scales probed by collider experiments and the Planck scale. Surprisingly, the answer is positive! Conceptually, the interacting renormalisation-group fixed point for the gravity–matter theory again gives a set of viable quantum field theories in terms of a fixed number of free parameters. First estimates conducted by Jan Pawlowski and coworkers at Heidelberg University suggest that this number is comparable to the number of free parameters in the SM.

In practice, one may then be tempted to make the following connection. Currently, observables probed by collider physics are derived from the SM effective field theory. Hence, they depend on the couplings of the effective field theory. The asymptotic-safety mechanism expresses these couplings in terms of the free parameters associated with the interacting fixed point. Once the SM effective field theory is extended to include operators of sufficiently high mass dimension, the asymptotic-safety dictum predicts highly non-trivial relations between the couplings parameterising the effective field theory. These relations can be confronted with observations that test whether the observables measured experimentally are subject to these constraints. This can either be provided by matching to existing particle-physics data obtained at the LHC, or by astrophysical observations probing the strong-gravity regime. The theoretical programme of deriving such relations is currently under development. A feasible benchmark, showing that the underlying physics postulates are on the right track, would then be to “post-dict” the experimental results already available. Showing that a theory formulated at the Planck scale is compatible with the SM effective field theory would be a highly non-trivial achievement in itself.

Showing that a theory formulated at the Planck scale is compatible with the SM effective field theory would be a highly non-trivial achievement in itself

This line of testing quantum gravity experimentally may be seen as orthogonal to more gravity-focused tests that attempt to decipher the quantum nature of gravity. Recent ideas in these directions have evolved around developing tabletop experiments that probe the quantum superposition of macroscopic objects at sub-millimetre scales, which could ultimately be developed into a quantum-Cavendish experiment that probes the gravitational field of source masses in spatial quantum superposition states. The emission of a graviton could then lead to decoherence effects which give hints that gravity indeed has a force carrier similar to the other fundamental forces. Of course, one could also hope that experiments probing gravity in the strong-gravity regime find deviations from general relativity. So far, this has not been the case. This is why particle physics may be a prominent and fruitful arena in which to also test quantum-gravity theories such as asymptotic safety in the future.

For decades, quantum-gravity research has been disconnected from directly relevant experimental data. As a result, the field has developed a vast variety of approaches that aim to understand the laws of physics at the Planck scale. These include canonical quantisation, string theory, the AdS/CFT correspondence, loop quantum gravity and spin foams, causal dynamical triangulations, causal set theory, group field theory and asymptotic safety. The latter has recently brought a new perspective on the field: supplementing the quantum-gravity sector of the theory by the matter degrees of freedom of the SM opens an exciting window through which to confront the construction with existing particle-physics data. As a result, this leads to new avenues of research at the intersection between particle physics and gravity, marking the onset of a new era in quantum-gravity research in which the field travels from a purely theoretical to an observationally guided endeavour.