The discovery of the Higgs boson at the LHC in 2012 changed the landscape of high-energy physics forever. After just a few short years of data-taking by the ATLAS and CMS experiments, this last piece of the Standard Model (SM) was proven to exist. Since then, the Higgs sector has been studied using a rapidly growing dataset and, so far, all measurements agree with the SM predictions within the experimental uncertainties. In parallel, a comprehensive programme of searches for beyond-SM processes has been carried out, resulting in strong constraints on new physics. A harvest of precise measurements of a large variety of processes, confronted with state-of-the-art theoretical predictions, has further supported the SM. However, the theory lacks explanations for, among others, the nature of dark matter, the cosmological baryon asymmetry and neutrino masses. Importantly, the Higgs sector is related to “naturalness” problems that suggest the existence of new physics at the TeV scale, which the LHC can probe.
The high-luminosity phase of the LHC (HL-LHC) will provide an order of magnitude more data starting from 2029, allowing precision tests of the properties of the Higgs boson and improved sensitivity to a wealth of new-physics scenarios. The HL-LHC will deliver to each of the ATLAS and CMS experiments approximately 170 million Higgs bosons and 120,000 Higgs-boson pairs over a period of about 10 years. By extrapolating Run 2 results to the HL-LHC dataset, this will increase the precision of most Higgs-boson coupling measurements: 2–4% precision on the couplings to W, Z and third-generation fermions; and approximately 50% precision on the self-coupling by combining the ATLAS and CMS datasets. The larger dataset will also give improved sensitivity to rare vector-boson scattering processes that will offer further insights into the Higgs sector.
These precision measurements could reveal discrepancies with the SM predictions, which in turn could inform us about the energy scale of beyond-SM physics. In addition to improving SM measurements, the upgraded detectors and trigger systems being developed and constructed for the HL-LHC era will enable direct searches to better target new physics with challenging signatures. To achieve these goals, it will be essential to achieve a detailed understanding of the detector performance as well as to measure the integrated luminosity of the collected dataset to 1% precision.
Rising to the challenge
To cope with the increased number of interactions when proton bunches collide at the HL-LHC, the ATLAS collaboration is working hard to upgrade its detectors with state-of-the-art instrumentation and technologies. These new detectors will need to cope with challenging radiation levels, higher data rates and an extreme high-occupancy environment with up to 200 proton–proton interactions per bunch crossing (see “Pileup” figure). Upgrades will include changes to the trigger and data-acquisition systems, a completely new inner tracker, as well as a new silicon timing detector (see “ATLAS Phase II” figure).

The trigger and data-acquisition system will need to cope with a readout rate of 1 MHz, which is about 10 times higher than today. To achieve this, ATLAS will use a new architecture with a level-0 trigger (the first-level hardware trigger) based on the calorimeter and muon systems. Building on the upgrades for Run 3, which started in July 2022, the calorimeter will include capabilities for triggering at higher pseudorapidity, up to |η| = 4. During HL-LHC running, the global trigger system will be required to handle 50 Tb/s as input and to decide within 10 μs whether each event should be recorded or discarded, allowing for more sophisticated algorithms to be run online for particle identification. All the detectors will require substantial upgrades to handle the additional acceptance rates from the trigger.
The readout electronics for the electromagnetic, forward and hadronic end-cap liquid-argon calorimeters, along with the hadronic tile calorimeter, will be replaced. The full calorimeter systems, segmented into 192,320 cells that are read out individually, will be read out for every bunch crossing at the full 40 MHz to provide full-granularity information to the trigger. This will require changes to both front-end electronics and off-detector components.
The muon system will also see significant upgrades to the on-detector electronics of the resistive plate chambers (RPCs) and thin-gap chambers (TGCs) responsible for triggering on muons, as well as the muon drift tubes (MDTs) responsible for measuring the curvature of the tracks precisely. The MDTs will also be used for the first time in the level-0 trigger decisions. These improvements will allow all data to be sent to the back-end at 40 MHz, removing the need for readout buffers on the detector itself. All hits in the detector will be used to perform trigger logic in hardware using field programmable gate-arrays. Additional improvements to increase the trigger acceptance for muons will come in the form of a new layer of RPCs to be installed in the inner barrel layer, along with new MDTs in the small sectors. The Muon New Small Wheel system was installed during Long Shutdown 2 (LS2) from 2019 to 2022 and is located inside the end-cap toroid magnet containing both triggering and precision tracking chambers. Additional RPC upgrades were also made in the barrel leading up to Run 3, and the TGCs will be upgraded in the endcap region of the muon system during LS3.
State-of-the-art tracking
The success of the research programme at the HL-LHC will strongly rely on the tracking performance, which in turn determines the ability to efficiently identify hadrons containing b and c quarks, in addition to tau and other charged leptons. Reconstructing individual particles in the HL-LHC collision environment with thousands of charged particles being produced within a region of about 10 cm will be very challenging. The entire tracking system, presently consisting of pixel and strip detectors and the transition radiation tracker, will be replaced by a new all-silicon pixel and strip tracker – the ITk. This will feature higher granularity, increased radiation hardness and readout electronics that allow higher data rates and a longer trigger latency. The new pixel detector will also extend the pseudorapidity coverage in the forward region from |η| < 2.5 to |η| < 4, increasing the acceptance for important physics processes like vector-boson fusion (see “Pixel perfection” image).
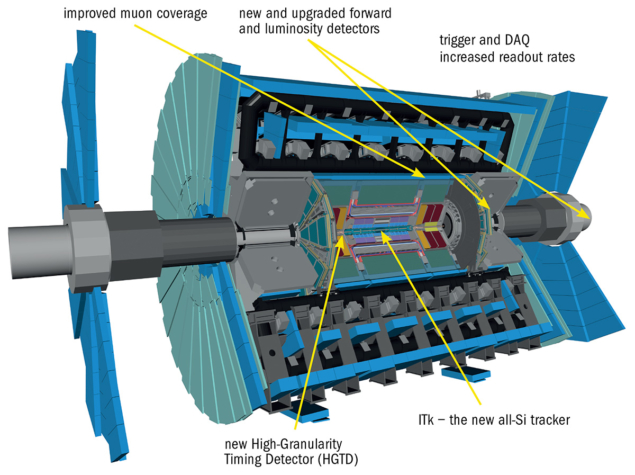
The ITk will comprise nine barrel layers, positioned at radii from 33 mm out to 1 m from the beam line, plus end-cap rings. It will be much more complex with respect to the present ATLAS tracker, featuring 10 times the number of strip channels and 60 times the number of pixel channels. The strip detectors will cover a total surface of 160 m2 with 60 million readout channels, and the pixels an area of 13 m2 with more than five billion readout channels. The innermost layer will be populated with radiation-hard 3D sensors, with pixel cells of 25 × 100 µm2 in the barrel part and 50 × 50 µm2 in the forward parts for improved tracking capabilities in the central and forward regions. Prototypes of the end-cap ring for the inner system and of the strip barrel stave are at an advanced stage (see “ITk prototyping” image). A unique feature of the trackers at the HL-LHC is that they will be operated for the first time with a serial powering scheme, in which a chain of modules is powered by a constant current. If the modules were to be powered in parallel, the high total current would lead to either high power losses or a large mass of cables within the volume of the detector, which would impact the tracking performance.
Given the challenging conditions posed by the HL-LHC, ATLAS will construct a novel precision-timing silicon detector, the High-Granularity Timing Detector (HGTD), which provides a time resolution of 30 to 50 ps for charged particles. The detector will cover a pseudorapidity range of 2.4 < |η| < 4 and will comprise two double-sided silicon layers on each side of ATLAS with a total active area of 6.4 m2. The precise timing information will allow the collaboration to disentangle proton–proton interactions in the same bunch crossing in the time dimension, complementing the impressive spatial resolution of the ITk. Low-gain avalanche diodes (see “Clocking tracks” image) provide timing information that can be associated with tracks in the forward regions, where they are more difficult to assign to individual interactions using spatial information. With a timing resolution six times smaller than the temporal spread of the beam spot, tracks emanating from collisions occurring very close in space but well-separated in time can be distinguished. This is particularly important in the forward region, where reduced longitudinal impact-parameter resolution limits the performance.

Building upon the insertable B-layer cooling system used since the start of Run 2, and to reduce the material budget, ATLAS will use a two-phase CO2 cooling system for the entire silicon ITk and HGTD detectors. These will allow the detectors to be cooled to around –35 °C during the entire lifetime of the HL-LHC. The low temperature is required to protect the silicon sensors from the expected high radiation dose received during their lifetime. Two-phase CO2 cooling is an environmentally friendly option compared to other suitable coolants. It provides a high heat transfer at reasonable flow parameters, a low viscosity (thus reducing the material used in the detector construction) and a well-suited temperature range for detector operations.
Luminous future
Precise knowledge of the luminosity is key for the ATLAS physics programme. To reach the goal of percent-level precision at the HL-LHC, ATLAS will upgrade the LUCID (Luminosity Cherenkov Integrating Detector) detector, a luminometer that is sensitive to charged particles produced at the interaction point. This is incredibly challenging given the number of interactions expected to be delivered by the machine, and the requirements on radiation hardness and long-term stability for the lifetime of the experiment. The HGTD will also provide online luminosity measurements on a bunch-by-bunch basis, and additional detector prototypes are being tested to provide the best possible precision for luminosity determination during HL-LHC running. Luminometers in ATLAS provide luminosity monitoring to the LHC every one to two seconds, which is required for efficient beam steering, machine optimisation and fast checking of running conditions. In the forward region, the zero-degree calorimeter, which is particularly important for determining the centrality in heavy-ion collisions, is also being redesigned for HL-LHC running.

The HL-LHC will deliver luminosities of up to 7.5 × 1034 cm–2s–1, and ATLAS will record data at a rate 10 times higher than in Run 2. The ability to process and analyse these data depends heavily on R&D in software and computing, to make use of resource-efficient storage solutions and opportunities that paradigm-shifting improvements like heterogeneous computing, hardware accelerators and artificial intelligence can bring. This is needed to simulate and process the high-occupancy HL-LHC events, but also to provide a better theoretical description of the kinematics.
New era
The Phase-II upgrade projects described are only possible through collaborative efforts between universities and laboratories across the world. The research teams are currently working intensely to finalise the designs, establish the assembly and testing procedures, and in some cases start construction. They will all be installed and commissioned during LS3 in time for the start of Run 4, currently planned for 2029.
To cope with the increased number of interactions when proton bunches collide at the HL-LHC, the ATLAS collaboration is working hard to upgrade its detectors with state-of-the-art instrumentation and technologies
The HL-LHC will provide an order of magnitude more data recorded with a dramatically improved ATLAS detector. It will usher in a new era of precision tests of the SM, and of the Higgs sector in particular, while also enhancing sensitivity to rare processes and beyond-SM signatures. The HL-LHC physics programme relies on the successful and timely completion of the ambitious detector upgrade projects, pioneering full-scale systems with state-of-the-art detector technologies. If nature is harbouring physics beyond the SM at the TeV scale, then the HL-LHC will provide the chance to find it in the coming decades.