Precision pins down the electron’s magnetism

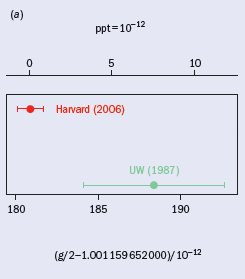
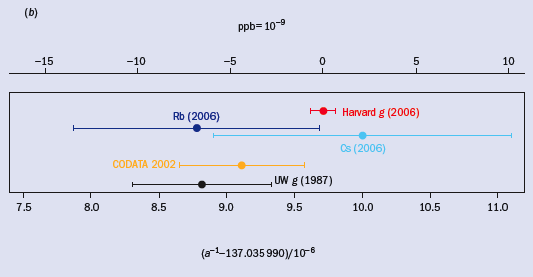
The electron’s magnetic moment has recently been measured to an accuracy of 7.6 parts in 10¹³ (Odom et al. 2006). As figure 1a indicates, this is a six-fold improvement on the last measurement of this moment made nearly 20 years ago (Van Dyck et al. 1987). The new measurement and the theory of quantum electrodynamics (QED) together determine the fine structure constant to 0.70 parts per billion (Gabrielse et al. 2006). This is nearly 10 times more accurate than has so far been possible with any rival method (figure 1b). Higher accuracies are expected, based upon convergence of many new techniques – the subject of a half-dozen Harvard PhD theses during the past 20 years. A one-electron quantum cyclotron, cavity-inhibited spontaneous emission, a self-excited oscillator and a cylindrical Penning trap contribute to the extremely small uncertainty. For the first time, researchers have achieved spectroscopy with the lowest cyclotron and spin levels of a single electron fully resolved via quantum non-demolition measurements, and a cavity shift of g has been directly observed.

Unusual features

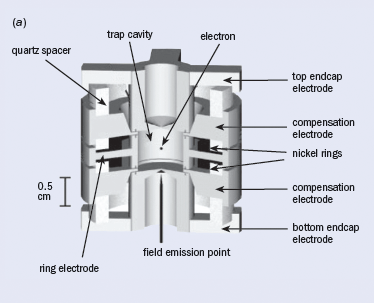
A circular storage ring is the key to these greatly improved measurements, but the storage ring is unusual compared with those at CERN, for example. To begin with it uses only one electron, stored and reused for months at a time. The radius of the storage ring is much less than 0.1 µm, and the electron energy is so low that we use temperature units to describe it – 100 mK. Furthermore, the electron does not orbit in a familiar circular orbit even though it is in a magnetic field; instead, it makes quantum jumps between only the ground state and the first excited states of its cyclotron motion – non-orbiting stationary states. It also makes quantum jumps between spin up and spin down states. Blackbody photons stimulate transitions between the two cyclotron ground states until we cool our storage ring to 100 mK to essentially eliminate them. The spontaneous emission of synchrotron radiation is suppressed because of its low energy and by locating the electron in the centre of a microwave cavity. The damping time is typically about 10 seconds, about 10²⁴ times slower than for a 104 GeV electron in the Large Electron–Positron collider (LEP). To confine the electron weakly we add an electrostatic quadrupole potential to the magnetic field by applying appropriate potentials to the surrounding electrodes of a Penning trap, which is also a microwave cavity (figure 2a).

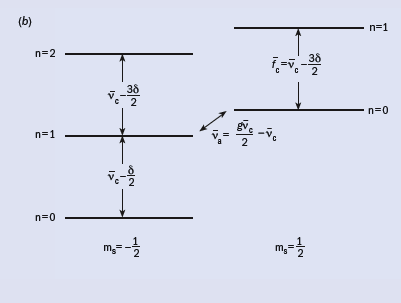
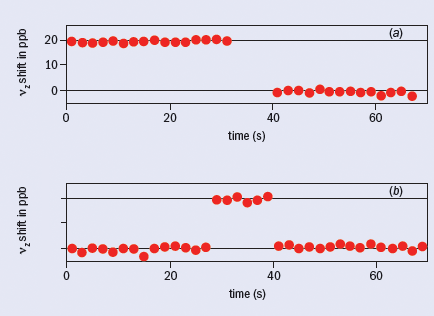
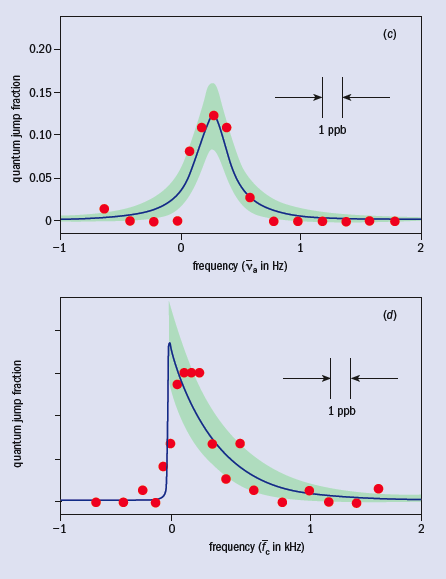
The lowest cyclotron and spin energy levels for an electron in a magnetic field are shown in figure 2b. (Very small changes to these levels from the electrostatic quadrupole and special relativity are well understood and measured, though they cannot be described in this short report.) Microwave photons introduced into our trap cavity stimulate cyclotron transitions from the ground state to the first excited state. The long cyclotron lifetime allows us to turn on a detector to count the number of quantum jumps for each attempt as a function of cyclotron frequency ν_c (figure 3d). A similar quantum jump spectroscopy is carried out as a function of the frequency of a radiofrequency drive at a frequency ν_a = ν_s – ν_c, which stimulates a simultaneous spin flip and cyclotron excitation, where ν_s is the spin precession frequency (figure 3c). The lineshapes are understood theoretically. One-quantum cyclotron transitions (figure 3b) and spin flips (figure 3a) are detected with good signal-to-noise from the small shifts that they cause to an orthogonal, classical electron oscillation that is self-excited.

The dimensionless electron magnetic moment is the magnetic moment in units of the Bohr magneton, ehbar/2m, where the electron has charge –e and mass m. The value of g is determined by a ratio of the frequencies that we measure, g/2 = 1 + νa/νc, with the result that g/2 = 1.00115965218085(76) [0.76 ppt]. The uncertainty is nearly six times smaller than in the past, and g is shifted downwards by 1.7 standard deviations (Odom et al. 2006).

What can be learned from the more accurate electron g? The first result beyond g itself is the fine structure constant, α = e²/4πε₀hbarc – the fundamental measure of the strength of the electromagnetic interaction, and also a crucial ingredient in our system of fundamental constants. A Dirac point particle has g = 2. QED predicts that vacuum fluctuations and polarization slightly increase this value. The result is an asymptotic series that relates g and α:

(Eq. 1)

g/2 = 1 + C₂(α/π) + C₄(α/π)² + C₆(α/π)³ + C₈(α/π)⁴
+ … a_µτ + a_hadronic + a_weak

According to the Standard Model, hadronic and weak contributions are very small and believed to be well understood at the accuracy needed. Impressive QED calculations give exact C₂, C₄ and C₆, a numerical value and uncertainty for C₈, and a small a_µτ. Using the newly measured g in equation 1 gives α^–1 = 137.035999710(96) [0.70 ppb] (Gabrielse et al. 2006). The total uncertainty of 0.70 ppb is 10 times smaller than for the next most precise methods (figure 1b), which determine α from measured mass ratios, optical frequencies, together with rubidium (Rb) or caesium (Cs) recoil velocities.

The second use of the newly measured electron g is in testing QED. The most stringent test of QED – which is one of the most demanding comparisons of any calculation and experiment – continues to come from comparing measured and calculated g-values, the latter using an independently measured α as an input. The new g, compared with equation 1 with α(Cs) or α(Rb), gives a difference δg/2 < 15 × 10sup>–12 (see Gabrielse 2006 for details and a discussion.) The small uncertainties in g/2 will allow a 10 times more demanding test if ever the large uncertainties in the independent α values can be reduced. The prototype of modern physics theories is thus tested far more stringently than its inventors ever envisioned – as Freeman Dyson remarks in his letter at the beginning of the article – with better tests to come.

The third use of the measured g is in probing the internal structure of the electron – limiting the electron to constituents with a mass m* > m/√(δg/2) = 130 GeV/c², corresponding to an electron radius R <1 × 10^–18 m. If this test was limited only by our experimental uncertainty in g, then we could set a limit m* > 600 GeV. This is not as stringent as the related limit set by LEP, which probes for a contact interaction at 10.3 TeV. However, the limit is obtained quite differently, and is somewhat remarkable for an experiment carried out at 100 mK.

The fourth use of the new electron g concerns measurements of the muon g – 2 as a way to search for physics beyond the Standard Model. Even though the muon g values have nearly 1000 times larger uncertainties than the new electron g, heavy particles – possibly unknown in the Standard Model – are expected to make a contribution that is much larger for the muon. However, this contribution would still be very small compared with the calculated QED contribution, which depends on α and must be subtracted out. The electron g provides α and a confidence-building test of the QED, both needed for the large subtraction.

CERN has long embraced particle physics at whatever energy scales are most appropriate for learning about fundamental reality. It is impressive that CERN is replacing the highest energy electron–positron collider, LEP, with the world’s highest energy proton collider, the Large Hadron Collider. Also at CERN, however, the lowest energy antiproton storage rings are also operating. One antiproton cooled to 4.2 K was used to show that the magnitudes of q/m for the proton and antiproton were the same to better than nine parts in 10¹¹ – the most stringent test of CPT invariance with a baryon system.

Now, these low-energy antiproton techniques are being used to make the coldest possible antihydrogen atoms, to be used for higher-precision tests of fundamental symmetries. It is fitting that the new measurement of the electron magnetic moment and the fine structure constant were carried out in the lab of a long-time CERN researcher, since they illustrate the power of low-energy techniques of the sort that we are applying to antihydrogen studies at CERN’s Antiproton Decelerator facility, the unique source of low-energy antiprotons.