The Daya Bay Reactor Neutrino Experiment has recently published a new measurement of the disappearance of electron antineutrinos emitted by nuclear reactors. The observation improves the precision of the mixing angle θ13 and the associated mass-squared difference |Δm2ee| by almost a factor of two.
This is the first measurement obtained with the completed Daya Bay detector configuration consisting of eight modular antineutrino detectors, providing a total target mass of 160 tonnes. The gadolinium-doped organic liquid scintillator detects electron antineutrinos via inverse beta decay (νe + p → e+ + n). Oscillation converts some of the νe to νμ and ντ, reducing the νe flux. Six commercial pressurised-water nuclear reactors (17.4 GW of thermal power in total) of the Daya Bay Nuclear Power Complex are an intense source, producing about 1021 electron antineutrinos per second. Four detectors located around 300 to 500 m from the reactors measure the initial νe rate from the reactors, while four detectors at around 1.6 km from the reactors observe the subsequent disappearance.
This result builds on previous measurements by the Daya Bay and RENO experiments, which provided the first proof that θ13 is nonzero. The improved statistical precision came from a 3.6 times increase in exposure, generating a data sample of 1.2 million νe interactions. The systematic uncertainties were also reduced through improved characterisation of the detectors and reduction of background.
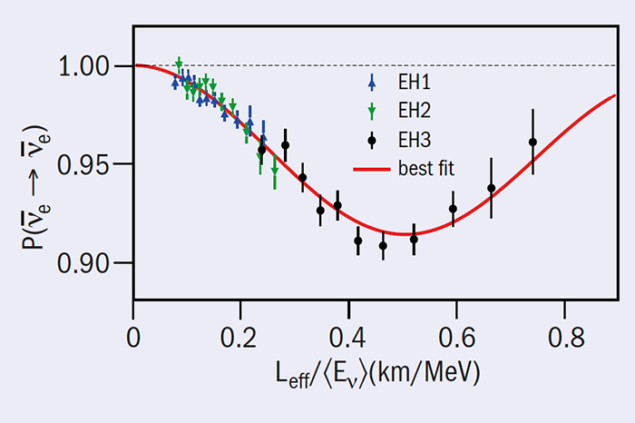
The analysis found sin2(2θ13) = 0.084±0.005 from the amplitude of anti-νe disappearance, while the energy dependence of this disappearance provided a measurement of oscillation frequency expressed in terms of the effective mass-squared difference |Δm2ee| = (2.42±0.11) × 10–3 eV2 (see figure 1). This is actually related to the two almost-equal neutrino mass-squared differences |Δm231| and |Δm231| = |Δm232 + Δm221|. One measure of how far neutrino physics has progressed is that the interpretation of this mixing parameter is now a step closer to being sensitive to the neutrino mass hierarchy. If the mass hierarchy is normal, then |Δm232| = (2.37±0.11) × 10–3 eV2, while if it is inverted, |Δm232| = (2.47±0.11) × 10–3 eV2.
The Daya Bay Reactor Neutrino Experiment continues to collect data, and aims at achiving a further factor of two improvement in precision by 2017.





