 Read article 'The coolest job in physics'
Read article 'The coolest job in physics'
 Read article 'The coolest job in physics'
Read article 'The coolest job in physics'
 Read article 'New pentaquark searches in beauty decays'
Read article 'New pentaquark searches in beauty decays'
A new analysis by LHCb of the open-charm hadrons in Λb decays was presented at the International Conference on Meson-Nucleon Physics and the Structure of the Nucleon
 Read article 'Pushing accelerator frontiers in Bern'
Read article 'Pushing accelerator frontiers in Bern'
The topical workshop “Gigahertz Rate and Rapid Muon Acceleration” showed how advanced accelerator concepts can jump-start dark-sector searches.
An iconic figure in modern science, Higgs in 1964 postulated the existence of the eponymous Higgs boson.
The directors of KEK, CERN, Fermilab and IHEP discussed a future global strategy at the 13th ICFA seminar.
A major upgrade to the AMS-02 tracking system planned for 2026 will bring key information relating to a mysterious excess of cosmic rays at high energies.
The oldest black hole found by the JWST and Chandra telescopes hints at the seeds of supermassive black-hole formation.
The papers assembled in this volume range in subject matter from dark-matter searches and gravitational waves to artistic and philosophical considerations.
 Read about 'CERN Courier magazine: get the latest issue'
Read about 'CERN Courier magazine: get the latest issue'
Browse the editor’s picks by downloading a PDF of the most recent issue of CERN Courier
 Read about 'In focus: enabling technologies'
Read about 'In focus: enabling technologies'
The platform technologies that underpin Europe’s large-scale research facilities
 Read article 'Tango for two: LHCb and theory'
Read article 'Tango for two: LHCb and theory'
The 13th Implications of LHCb measurements and future prospects workshop showcased mutual enthusiasm between the experimental and theoretical communities
 Read article 'Education and outreach in particle physics'
Read article 'Education and outreach in particle physics'
A celebration of the opening of CERN Science Gateway, a new flagship centre for science education and outreach.
 Read article 'Balancing matter and antimatter in Pb–Pb collisions'
Read article 'Balancing matter and antimatter in Pb–Pb collisions'
The ALICE collaboration has placed stringent limits on models describing baryon-number transport effects.
 Read article 'Belle II back in business'
Read article 'Belle II back in business'
Having emerged from a scheduled long shutdown, the upgraded Belle II detector in Japan recorded its first collisions on 20 February.
 Read article 'Iodine vapours impact climate modelling'
Read article 'Iodine vapours impact climate modelling'
Climate models are missing an important source of aerosol particles in polar and marine regions, according to new results from the CLOUD experiment at CERN.
 Read article 'The promise of laser-cooled positronium'
Read article 'The promise of laser-cooled positronium'
In demonstrating laser cooling of a purely leptonic matter-antimatter system, the AEgIS collaboration opens new possibilities for antimatter research.
 Read article 'Beams back for a bumper year'
Read article 'Beams back for a bumper year'
For the LHC, the aim during 2024 is to accumulate an integrated luminosity of up to 90 inverse femtobarns.
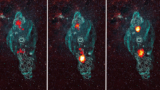 Read article 'Potent accelerators in microquasar jets'
Read article 'Potent accelerators in microquasar jets'
H.E.S.S opens exciting possibilities in the search for galactic cosmic-ray sources at PeV energies and extragalactic ones at EeV energies.
 Read article 'The people factor'
Read article 'The people factor'
The FCC collaboration beckons individuals and institutions to contribute to the next chapter in exploring the fundamental laws and building blocks of the universe.
 Read article 'Tunnelling to the future'
Read article 'Tunnelling to the future'
Weaving through the molasse and limestone beneath Lake Geneva and around Mont Salève, the Future Circular Collider would constitute a major global civil-engineering project in its...
 Read article 'Machine matters'
Read article 'Machine matters'
From the latest accelerator designs to their estimated cost and long-term societal returns, the Courier gathers the key takeaways so far from the Future Circular Collider feasibili...
 Read article 'Advancing hardware'
Read article 'Advancing hardware'
Snapshots of the latest developments in FCC-ee vacuum, radio-frequency, magnet and alignment technologies.