Johann Rafelski and Torleif Ericson recall Rolf Hagedorn’s discovery of a limiting temperature – in effect a melting point for hadrons – and its influence on the physics of strong interactions.

Collisions of particles at very high energies generally result in the production of many secondary particles. When first observed in cosmic-ray interactions this effect was unexpected, but it led to the idea of applying the wide body of knowledge of statistical thermodynamics to multiparticle production processes. Prominent physicists such as Enrico Fermi, Lev Landau and Isaak Pomeranchuk made pioneering contributions to this approach, but because difficulties soon arose it did not initially become the mainstream for the study of particle production. However, it was natural for Rolf Hagedorn to turn to the problem.
Hagedorn, who died earlier this year, had an unusually varied educational and research background, which included thermal, solid-state, particle and nuclear physics. His initial work on statistical particle production led to his prediction, in the 1960s, of particle yields at the highest accelerator energies at the time at CERN’s proton synchrotron. Though there were few clues on how to proceed, he began by making the most of the “fireball” concept, which was then supported by cosmic-ray studies. In this approach all the energy of the collision was regarded to be contained within a small space-time volume from which particles were radiated, as in a burning fireball.
Several key ingredients brought from early experiments helped him to refine the approach. Among these observations, the most noticeable was the limited transverse momentum of the overwhelming majority of the secondary particles. Also, the elastic scattering cross-section at large angles was found to drop exponentially as a function of incident energy. Such behaviour strongly suggested an inherently thermal momentum distribution.
However, many objections were raised in these pioneering days of the early 1960s. What might actually be “thermalized” in a high-energy collision? Applying straightforward statistical mechanics gave too small a yield of pions. Moreover, even if there was a thermalized system in the first place, why was the apparent temperature constant? Should it not rise with incident beam energy?
It is to Hagedorn’s great credit that he stayed with his thermal interpretation, solving the problems one after the other. His particle-production models turned out to be remarkably accurate at predicting yields for the many different types of secondaries that originate in high-energy collisions. He understood that the temperature governing particle spectra does not increase, because as more and more energy is poured into the system new particles are produced. It is the entropy that increases with the collision energy. If the number of particles of a given mass (or mass spectrum) increases exponentially, the temperature becomes stuck at a limiting value. This is the Hagedorn temperature TH. It is nearly 160 MeV, about 15% above the mass of the lightest hadron, the pion.
Since the more massive resonances eventually fragment into less massive ones to yield the observed secondary particles as the “bottom line”, this solved the problem of the pion yield. The factor 1/n!, which originated in the quantum indistinguishability of identical particles, had plagued the statistical calculations that focussed on pions only. Now it had become unimportant as each one of the many states was unlikely to have a population, n, exceeding 1. At long last agreement between experiment and statistical calculations prevailed.
The statistical bootstrap model
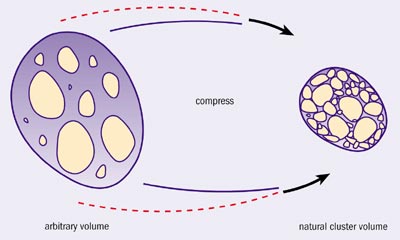
Once the physical facts had been assembled, Hagedorn turned his attention to improving their theoretical interpretation, and in considering the experimental finding that the formation of resonances dominates the scattering cross-section, he proposed the statistical bootstrap model (SBM). In a nutshell, in the SBM each of the many resonant states into which hadrons can be excited through a collision is itself a constituent of a still heavier resonance, whilst also being composed of lighter ones. In this way, when compressed to its natural volume, a matter cluster consisting of hadron resonances becomes a more massive resonance with lighter resonances as constituents, as shown in figure 1.
One day in 1964, one of us (TE) ran into Hagedorn, who was bubbling over to a degree we had not seen before. His eyes were lit up as he described all these fireballs: fireballs going into fireballs living on fireballs forever and all in a logically very consistent way. This must have been soon after he had invented the statistical bootstrap. He gave the impression of a man who had just found the famous philosophers’ stone, and that must have been exactly how he felt about it. Clearly Hagedorn immediately recognized the importance of the novel idea he had introduced. It was very interesting to observe how deeply he felt about it from the very beginning.
Using the SBM approach for a strongly interacting system, Hagedorn obtained an exponentially rising mass spectrum of resonant states. Today, experimental results on hadronic level counting reveal up to almost 5000 catalogued resonances. They agree beautifully with theoretical expectations from the SBM, and as our knowledge has increased, the observed mass spectrum has become a better exponential, as illustrated in figure 2. The solid blue line in figure 2 is the exponential fit to the smoothed hadron mass spectrum of the present day, which is represented by the short-dashed red line. Note that Hagedorn’s long-dashed green line of 1967 was already a remarkably good exponential. One can imagine that the remaining deviation at high mass in the top right corner of the figure originates in the experimental difficulties of discovering all these states.
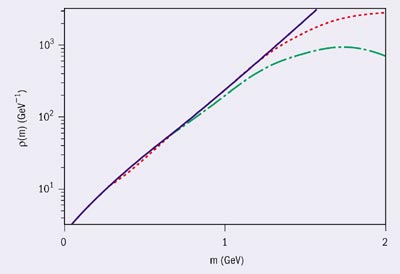
The important physics message of figure 2 is that the rising slope in the mass spectrum is the same as the falling slope of the particle momentum spectra. The momentum spectra originate in the thermalization process and thus in reaction dynamics; the mass spectrum is an elementary property of strong interactions. The SBM provides an explanation of the relationship between these slopes, and explains why the temperature is bounded from above. Moreover, since the smallest building block of all hadronic resonances is the pion, within the SBM one can also understand why the limiting temperature is of the same magnitude as the smallest hadron mass TH ≈ mπ.
Today the Hagedorn temperature TH is like a brand name, and the concept of an exponentially rising mass spectrum is part of our understanding of hadron phenomena, which can be understood using approaches different from the SBM, such as that offered by dual models. However, when first proposed the SBM was looked upon with considerable scepticism, even within the CERN Theory Division where Hagedorn worked. As time has gone by, the understanding of the particle-production process that Hagedorn brought about has grown in significance, such is the sign of truly original work, of something that really had influence on our thinking. Hagedorn’s article (Hagedorn 1965), which introduced the statistical bootstrap model of particle production and placed the maximum temperature in the vocabulary of particle physics, has found a place among the most cited physics papers.
The accurate description of particle production, through the conversion of energy into matter, has numerous practical implications. Even in the very early days, Hagedorn’s insight into the yields and spectra of the produced secondaries showed that neutrino beams would have sufficient flux to allow a fruitful experimental program, and this gave a theoretical basis for the planning of the first neutrino beams constructed at CERN.
Quark-gluon plasma
At the same time that the SBM was being developed, the newly discovered quarks were gaining acceptance as the building blocks of hadrons. While Hagedorn saw a compressed gas of hadrons as another hadron, in the quark picture it became a drop of quark matter. In quark matter at high temperatures gluons should also be present and as the temperature is increased asymptotic freedom ensures that all constituents are interacting relatively weakly. There seems to be nothing to stop a dense assembly of hadrons from deconfining into a plasma of quarks and gluons. It also seems that this new state of matter could be heated to a very high temperature, with no limit in sight. So what is the meaning of the Hagedorn temperature in this context?
In the SBM as conceived before quarks, hadrons were point particles. A subtle modification is required when considering quarks as building blocks. Hadrons made of quarks need a finite volume that grows with hadron mass. One of us (JR) worked on this extension of the SBM with Hagedorn at the end of the 1970s and in the early 1980s. We discovered that at the Hagedorn temperature, finite-size hadrons dissolve into a quark-gluon liquid. Both a phase transition and a smoother transformation are possible, depending on the precise nature of the mass spectrum. The most physically attractive alternative was a first-order phase transition. In this case the latent heat is delivered to the hadron phase at a constant Hagedorn temperature TH. A new phase is then reached wherein the hadron constituents – the quarks and the gluons – are no longer confined. The system temperature can now rise again.
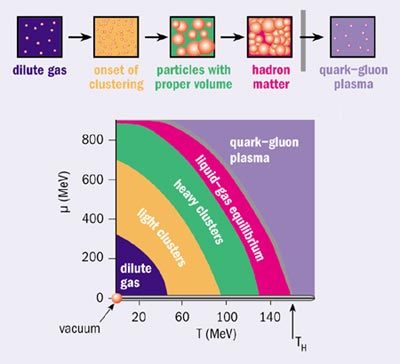
Within the study of hot hadronic matter today, the Hagedorn temperature is understood as the phase boundary temperature between the hadron gas phase and the deconfined state of mobile quarks and gluons (see figure 3). Several experiments involving high-energy nuclear collisions at CERN’s Super Proton Synchrotron (SPS) and at RHIC at the Brookhaven National Laboratory are testing these new concepts. Nuclei, rather than protons, are used in these experiments in order to maximize the volume of quark deconfinement. This allows a clearer study of the signature of the formation of a new phase of matter, the quark-gluon plasma (QGP).
The current experimental objective is the discovery of the deconfined QGP state in which the hadron constituents are dissolved. This requires the use of novel probes, which respond to a change in the nature of the state of matter within the short time available. More precisely, the heating of hadronic matter beyond the Hagedorn temperature is accompanied by a large collision compression pressure, which is the same in magnitude as the pressure in the very early universe. In the subsequent expansion, a collective flow velocity as large as 60% of the velocity of light is exceeded at RHIC. The expansion occurs on a timescale similar to that needed for light to transverse the interacting nuclei.
In the expansion-cooling process of QGP formed in nuclear collisions, the Hagedorn temperature is again reached after a time that corresponds to the lifespan of a short-lived hadron. A break up – that is, hadronization – then occurs and final-state hadrons emerge. Hagedorn was particularly interested in understanding the hadronic probes of QGP produced in hadronization. He participated in the initial exploration of the strangeness flavour as a signal of QGP formation.
In February 2000 the totality of intriguing experimental results obtained at the SPS over several years was folded into a public announcement stating that the formation of a new phase of matter was their best explanation. The key experimental results, including, in particular, strangeness and strange antibaryon enhancement, agreed with the theoretical expectations that were arrived at when one assumes that the QGP state was formed.

In mid-June 2003 the researchers at RHIC announced results that show that this new phase of matter is highly non-transparent to fast quarks, which is once more along the lines of what is expected for QGP. Many researchers believe that the deconfined phase has therefore been formed both at the SPS and at RHIC. The thrust of current research is to identify the conditions that are necessary for the onset of QGP, and to understand the initial reaction conditions in dense matter. In 2007 when a new domain of collision energy becomes accessible at CERN’s Large Hadron Collider, hot QGP in conditions similar to those present in the early universe will be studied.
In the next few years, the study of hadronic matter near the Hagedorn temperature will also dominate experimental efforts in the field of nuclear collisions, in particular at the new international experimental facility to be built at the GSI laboratory in Darmstadt, Germany. The richness of the physics at hand over the coming years is illustrated in the phase diagram in figure 3, which was obtained from the study of the SBM. Here, the domain is spanned by the temperature, T, and the baryochemical potential, µ, which regulates the baryon density.
In almost 50 years the understanding of the physics related to the Hagedorn temperature has changed. In the beginning it was merely the maximum temperature seen in proton-proton collisions. It then became the SBM inverse slope of the mass spectrum. Today, it denotes the phase boundary between hadron and quark matter. Moreover, as recent work in string theory has shown, Rolf Hagedorn will not only be remembered for the physics of hot hadronic matter: his name is already attached to a more general family of elementary phenomena that originate in the methods he developed in the study of strong interaction physics.
Further reading
R Hagedorn 1965 Nuovo Cim. Suppl. 3 147.





