Recent astronomical observations have raised the possibility that the natural constants are time-dependent. Harald Fritzsch considers the case for inconstant constants.
The natural constants are to some extent abnormal features of the theories considered today. On one hand they are needed to describe the theories, but on the other hand nobody understands their rather strange values. Indeed, no-one knows if they are accidents, or whether they can be calculated from some basic principles – a question that ranks in the top 10 unsolved problems for string theorists.

Recent observations in astrophysics suggest that α, the fine structure constant (see “The magic number ” box), which is of fundamental importance in describing the electromagnetic interaction, was in earlier periods a little smaller than today. A research group from Australia, the UK and the US analysed the spectra of distant objects, obtained in particular at the Keck I telescope in Hawaii. They studied around 150 quasars, some of them about 11 billion light-years away (Webb et al. 2001). The redshifts of the objects varied between 0.5 and 3.5, which corresponds to ages varying between 23 and 87% of the age of the universe. The team used the so-called “many multiplet” method – in particular on the spectra of iron, nickel, magnesium, zinc and aluminium – and found a value of α at early times of close to 1/137.037, as opposed to near 1/137.036, as is observed today. This is a small departure – the observations indicate Δα/α = (-0.72 ± 0.18) x 10-5 – but it could have important consequences for theory.

The idea that certain fundamental constants are not constant at all, but have a certain cosmological time dependence, is not new. In the 1930s, the idea was discussed by Paul Dirac (Dirac 1937) and by Arthur Milne (Milne 1937), but with respect to the gravitational constant. Dirac wrote his article at that time during the holiday following his marriage, prompting his colleague George Gamow to remark: “That happens if people get married.”
At around the same time, Pascal Jordan discussed the possibility that other constants could also be time-dependent (Jordan 1937; 1939), but he refused to consider that the constant of the weak interactions or the ratio of the electron and proton mass might be time-dependent. Later, Lev Landau considered the possibility of a time dependence of α in connection with the renormalization of the electric charge (Landau 1955).
We can also say something about the time dependence of α by studying the remains of the natural reactor found near Oklo in Gabon, West Africa, which was in operation about 2 billion years ago. The isotopes of the rare earths, for example of samarium, were produced by the fission of uranium. The observed distribution of the isotopes today is consistent with calculations, assuming that the isotopes were exposed to a strong neutron flux. The value of α that one can deduce agrees rather precisely with the value observed today. The change of α has to be smaller than about 10-17 per year, according to the calculations by Thibault Damour and Freeman Dyson (Damour and Dyson 1996). Taking the astrophysics values and the Oklo data together, one arrives at the curious possibility that the value of α increased in the early universe by a few 10-5, but has remained constant during the past 2 billion years.
However, the significance of the Oklo data becomes less clear if, besides a change of α, changes of other parameters are also considered, for example the parameters of the strong interaction. The limit for the change in α comes from the observation that the cross-section for the scattering of thermal neutrons off samarium-149 is dominated by a nuclear resonance. The position of this resonance cannot have changed during the past 2 billion years, according to experimental data, and this limits the change of α. Because of the Coulomb repulsion in the nucleus, an increase of α would lead to an increase in the energy of the resonance. However, a change of the strong coupling constant, αs, could easily compensate for this effect.
Observing a time dependence of α is certainly an important, if not spectacular result, but a certain measure of scepticism should be kept. If the fundamental constants really do depend on time, rather severe consequences are expected for cosmological evolution since the Big Bang. Nevertheless, the data should be taken seriously, as there are no strong theoretical arguments why the constants should really be absolutely constant.
Grand unification
In the Standard Model of the elementary particles, the overall gauge group is given by SU(3) x SU(2) x U(1), and the electromagnetic and weak interactions are described by the subgroup SU(2) x U(1). Both the Z boson and the photon are superpositions of the neutral SU(2) component and the U(1) boson. This means that the electromagnetic coupling constant e, i.e. the fine structure constant, is not a basic coupling constant. It is related to the basic coupling constant of the SU(2) theory by the relation: e = g/2 sinθw. Experiments give the value of the weak angle, renormalized at the mass of the Z boson, as sin2θw(Q2 =Mz2) = 0.2113 ± 0.00015.
The three coupling constants of the strong and the electroweak interactions vary with energy, but they converge if they are extrapolated to very high energies (about 1016 GeV). This is precisely what one expects if the three interactions are unified. Such a “grand unification” is realized if the gauge groups of the strong interactions, i.e. the colour group SU(3) and the two gauge groups of the electroweak interactions, SU(2) and U(1), are subgroups of a simple group that unifies the three interactions.

Two groups are of particular interest – SU(5) (Georgi and Glashow 1974) and SO(10) (Fritzsch and Minkowski 1975). The group SU(5) has the property that the fermions of one generation are described by two representations. The group SO(10) has an interesting property: the leptons and quarks of one generation can be described by a single representation, the so-called spinor representation or 16-representation. For example, for the fermions of the first generation, this contains six quarks (u and d in three colours) and six antiquarks, together with the electron, positron, a left-handed electron-neutrino and a right-handed electron-neutrino. Note the introduction, in addition to the normal left-handed neutrino, of a right-handed neutrino, which in the normal weak interaction does not appear. However, its existence is important for the appearance of a mass for the neutrino. In fact, in the SO(10) theory, one expects in general that neutrinos have a mass, in accordance with evidence from current experiments.
The coupling constants of the Standard Model seem to converge if extrapolated to high energies. It turns out that in the SU(5) model, they do not come together at one point, but in models based on the SO(10) group a convergence can be achieved, since in those theories a new energy scale besides the unification energy plays a role at high energies. However, one can also achieve a convergence of the coupling constants in the SU(5) model, if supersymmetry is realized at energies above about 1 TeV. The contributions of the supersymmetric particles change the renormalization coefficients so that a convergence takes place at about 1016 GeV.
If we take the idea of grand unification seriously, it implies that the variation of α in time should go parallel to a variation in time of the unifying coupling constant gun – otherwise the grand unification would only work at a particular time, which does not make much sense. Consequently we would expect that all three coupling constants g1, g2 and g3, would be time-dependent. Of particular interest here is a time dependence of the QCD coupling, i.e. of αs, since this coupling determines the hadronic mass scale and many other parameters in hadronic and nuclear physics.
Consider now the behaviour of αs in lowest order only. It is given by the renormalization group equations as follows:

Here µ is a reference scale, ß0 = -11 +2/3 x nf (nf is the number of quark flavours), and Λs is the QCD scale parameter.
Experiments, especially the measurements carried out at LEP, give αs = 0.116 + 0.003/-0.005 (exp.) ± 0.003 (theory). A typical value for the scale parameter is Λs = 213 + 38/-35 MeV. Of course, if αs is not only a function of the reference scale, but also of time, then the scale parameter Λs also varies with time. We find for the time dependence:
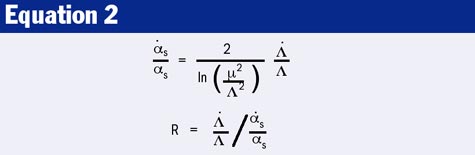
The relative time dependencies are related by: δΛ/Λ = (δαs/αs) ln (µ/Λ). It follows that the relative change of αs cannot be uniform, i.e. identical for all reference scales, but must change logarithmically if the reference scale changes. We could, for example, consider a relative change of αs at very high energies, for example close to the energy where the grand unification sets in. The corresponding change of Λ would then be larger by a factor ln (µ/Λ) =~ 38.
Further time dependencies
In QCD, the proton mass as well as all other hadronic mass scales are proportional to Λ, if the quark masses are neglected. In fact, the masses of the light quarks, mu, md and ms, are different from zero, but the mass terms contribute only a little to the total mass, typically less than 10%. We shall not consider these contributions, and we shall also neglect a small contribution of electromagnetic origin to the nucleon mass.
So if the QCD coupling or the QCD scale parameter changed in time, we would expect a corresponding change in time of the nucleon mass and of the masses of the atomic nuclei (Calmet and Fritzsch 2002). Such a change could be observed through a measurement of the mass ratio me/mp. Since a change in the QCD parameters would not influence the electron mass, the result would be a change in this mass ratio.
Independent of the details of the unification scheme, one would expect that a change in time would in particular imply a change in time of the unified coupling constant, defined for example at the point of unification. In order to be specific, consider as an example SU(5) theory with supersymmetry, which is broken at about 1 TeV to yield the Standard Model. The change in time of the three gauge couplings is given in figure 1. The unification takes place at ΛGUT = 1.5 x 1016 GeV, where the coupling constant is αun = 0.03853.
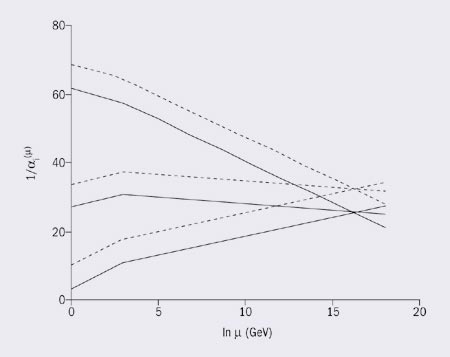
A variation in time can occur through a time dependence of the unified coupling constant, but also through a time dependence of the energy at which unification takes place. In the case where only the coupling constant varies with time, one finds that the time change of α and αs are related. In fact, both time changes are linked to each other by the ratio 8/3 x (α/αs), which is about 1/10. That is, the time change of the strong coupling constant is roughly an order of magnitude larger than the time change of the electromagnetic coupling constant.
In the case where the coupling constant remains invariant, but the energy at which the unification takes place depends on time, one finds that the time change of the scale Λ for the strong interactions is about 31 times larger than the time change of α, but has the opposite sign. This is interesting. While α increases with a rate of about 10-15 per year, Λ and the nucleon mass both decrease at a rate of about 2 x 10-14 per year. At the same time, the magnetic moments of the proton and of the nuclei would slowly increase, at a rate of about 3 x 10-14 per year.
Future observations
A change in time of the proton mass and of α could be observed through precise measurements in quantum optics. The wavelength of light emitted in hyperfine transitions, for example in the transitions that are measured in caesium clocks, is proportional to α4me/Λ, which would be time-dependent via both α and Λ. On the other hand, the wavelength of light that is generated in atomic transitions depends only on α, and would vary in time accordingly. We would expect that light emitted in hyperfine transitions should vary in time about 17 times more strongly than light emitted in normal atomic transitions, but in the opposite direction, i.e. the atomic wavelength becomes smaller with time, but the hyperfine wavelength increases.
The second is currently defined as the duration of 6,192,631,770 cycles of microwave light, which is emitted in the hyperfine transitions of caesium-133. If Λ were to change in time, it would mean that the flow of time, which is measured with caesium clocks, does not fully correspond to the flow of time tested in atomic transitions. Experiments to look for an effect of this kind will be carried out soon at the Max-Planck-Institute for Quantum Optics in Munich, under the leadership of Theodor Haensch.
If such an effect is discovered, it will be important to determine the sign and magnitude of the double ratio R (equation 2). If one obtains R ~ -20, it would be a strong indication for unification of the strong and electroweak interactions. Furthermore, this value would be of great interest in better understanding any changes in the constants of nature with time.

The fine structure constant α is composed of e, h/2π and c. Thus, if α depends on time, it would mean that at least one of these numbers depends on time. Today we usually start with the hypothesis that h/2π and c are fundamental unities, which in suitable systems can also be set to 1. Thus a change of time of α would correspond to a change of e.
In the theories of “superstrings”, one has, in fact, an additional motivation that fundamental constants are not really constant. In these theories, dimensionless coupling constants such as α are related to functions of vacuum expectation values of scalar fields, which could easily depend on time. Furthermore, a time dependence could also easily arise if, besides the three space dimensions, there are more hidden dimensions.
It would be particularly interesting to find information about the coupling constants such as α or αs in the early universe. A direct measurement is not possible, but recent measurements of the cosmic microwave background, which has its origin in the early universe, do not show within an accuracy of about 10% any time dependence of α. Data from the MAP satellite, launched in 2001, will allow us to improve this limit or to find an effect. Further hints towards a time dependence of α or αs, or both, will have important consequences.
Further reading
X Calmet and H Fritzsch 2002 Phys. Lett. 540 173.
T Damour and F Dyson 1996 Nucl. Phys. B 480 37.
P M Dirac 1937 Nature 192 (325) 8.
H Fritzsch and P Minkowski 1975 Annals Phys. 93 193.
H Georgi and S L Glashow 1974 Phys. Rev. Lett. 32 438.
P Jordan 1937 Naturwiss. 25 513.
P Jordan 1939 U. Physik 1113 660.
L D Landau 1955 in W Pauli (ed.) Niels Bohr and the Development of Physics (McGraw-Hill, New York) p52.
E A Milne 1937 Proc. Roy. Soc. A 3 242.
J K Webb et al. 2001 Phys. Rev. Lett. 67 091301.





