General relativity made Einstein an instant success. However, reconciling the theory with quantum mechanics has proved to be a formidable task, which is far from complete. Nick Mavromatos explains.
The theory of general relativity provides an appealing way of understanding gravitational dynamics, by perceiving the nature of the gravitational force as being due to a non-trivial geometry of space-time.
The predictions of this revolutionary theory were verified experimentally almost immediately after its proposition, making Einstein an instant success. However, general relativity is a purely classical theory. Quantizing it has so far proved to be a formidable task, which is far from complete. Due to the theory’s unconventional form, as compared with the rest of the fundamental interactions in nature, a mathematically consistent and complete theory of quantum gravity remains elusive.
Theoretical approaches
The discovery of string theory opened up novel and unconventional ways of attacking the problem. By viewing gravitons, the hypothesized carriers of the gravitational interaction, as one of the excitations of the (closed) superstring ground state, the first mathematically consistent framework of unification of gravity with the rest of the fundamental interactions (strong and electroweak) could be achieved. However, this approach is also incomplete. The last decade has revealed a much richer structure of the theory, consisting not only of one-spatial-dimensional objects (strings), but also of higher-dimensional membrane solitonic structures (such as D-branes) whose dynamics are still not well understood. String theory itself, however, has not yet given a complete answer to the question of what happens when quantum matter interacts with singular space-time backgrounds such as black holes.
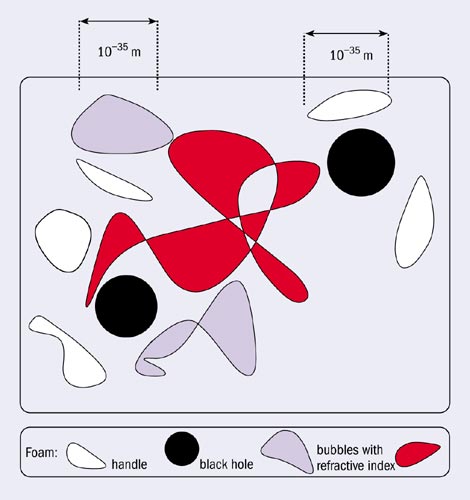
In the framework of local field theory, John Wheeler and Stephen Hawking have suggested that microscopic quantum space-time fluctuations of black hole type, with size of the order of the Planck length (10-35 m), characterize the quantum-gravity vacuum, giving it a “space-time foamy” nature (figure 1). Interaction of matter with such backgrounds may result in the loss of quantum coherence. This in turn could lead to significant deviations from the standard quantum-mechanical behaviour of matter particles, even at scales much lower than the characteristic quantum-gravity (Planck) energy scale of 1019 GeV. This is because gravity is a non-renormalizable interaction, with a dimensionful coupling constant, and so it may manifest itself at much lower scales. An example of such a phenomenon is provided by the so-called charge-parity (CP) discrete symmetry, whose violation manifests itself at scales much lower than the characteristic scale of the underlying weak interactions responsible for the effect.
However, the existence of space-time foam effects has been questioned, in particular by string theorists. In superstrings, for certain specific classes of black holes, it is possible to count precisely the microstates that constitute the internal black hole structure by virtue of string dualities (certain discrete gauge symmetries of strings). This has prompted the conjecture that in string theory there is no loss of information during the interaction of string matter with singular space-time backgrounds, and therefore no loss of quantum coherence. If this is true for every singular space-time background, it would be a manifestation of the so-called holographic conjecture of ‘t Hooft and Susskind, according to which any information that enters the horizon of a black hole (a sort of space-time boundary) is encoded on the boundary and no information is lost.
Unfortunately, the situation may not be that simple. Physicists have so far been unable to demonstrate the holographic principle rigorously outside certain restricted classes of stringy black hole backgrounds. Moreover, within the modern context of brane theory there have been theoretical arguments demonstrating that it is impossible to describe the formation of a black hole by collapsing string matter, or the final stage of its evaporation by purely unitary quantum methods.
Liouville strings
It is at this point that alternative paths within the string framework have been proposed. One is the so-called Liouville (non-critical) string, a sort of non-equilibrium string theory allowing for a stochastic description of space-time foam backgrounds. In such models, gravitational degrees of freedom, unobservable by low-energy observers, constitute an “environment” that results in the non-equilibrium nature of the underlying string theory. Technically speaking, the foam background is not conformal (its world-sheet dynamics are not invariant under special local-scale transformations). Nevertheless, with certain restrictions such theories are still mathematically consistent.
Time plays a particularly special role in Liouville strings, where it is identified with a world-sheet renormalization-group scale, the Liouville mode itself. In such a picture, the irreversibility of the temporal flow is guaranteed by powerful remormalization-group-flow theorems of the 2D world-sheet geometry. Such an irreversible flow has immediate consequences for entropy production, associated with the non-equilibrium nature of the Liouville string.
On the other hand, it has been argued that a Liouville-string irreversible time flow may play an important role in cosmological scenarios, in particular in relaxation models of the universe, allowing for the possibility of an exit from an accelerating universe (de Sitter) phase, as well as a relaxing-to-zero vacuum energy. Such models provide a natural explanation for the smallness of the present-era value of the cosmological constant, consistent with recent astrophysical claims. It is therefore interesting to note that the same mathematical framework of the Liouville string, which provides a picture for the space-time foam, can also describe a cosmological model of the universe with correct phenomenology.
The fundamental issue of the nature of time probably holds the key to unravelling a consistent theory of quantum gravity. The relevant phenomenology, therefore, which has already enjoyed almost two decades of intense research, may also contribute significantly to an understanding of such fundamental questions.
For the time being, however, string theories seem to suffer from an important drawback, which probably prevents a complete understanding of quantum gravity issues within this framework. This is their background dependence – the fact that the whole formalism of strings, at least so far, is based on specific space-time backgrounds. A satisfactory theory of quantum gravity is expected to be capable of describing the generation of the space-time structure in a dynamical way from more fundamental units. This may be possible in string field theory, but the subject is at present in its infancy.
This property of background independence seems to characterize another major approach towards the quantization of gravity, the so-called loop quantum gravity. This is a way of canonically quantizing gravity starting from a theory of abstract “spin-foam networks”. These are the fundamental units from which the fabric of space-time is generated dynamically in a mathematically self-consistent and elegant formalism, and hence the approach is background independent by design. At present it is not known whether the theory is related to (Liouville) string theory. Moreover, no significant progress has been made towards an understanding of issues relating to information loss in quantum black hole backgrounds or the unification of gravity with the rest of the interactions. There is intense ongoing research in this field, and such questions may soon be tackled. For our purposes it is sufficient to mention that loop quantum gravity, like Liouville strings, appears to provide a theoretical framework for a discussion of stochastic space-time foam dynamics.
Experimentally falsifiable predictions
It is of primary importance to attempt to make physical, experimentally falsifiable predictions from these different frameworks of quantum gravity. At first sight this may seem wishful thinking for any theory of quantum gravity, whose fundamental length scale is far too small to be directly visible. However, since gravity is a non-renormalizable interaction, effects associated with it might be visible at energy scales much lower than the Planck scale.

One possible imprint of quantum gravity at lower scales might be the loss of quantum coherence that characterizes certain models of quantum gravity. The imprint would be a violation of CPT symmetry (T=time reversal), whose conservation is a theorem of any local unitary field theory without gravity, but whose failure is almost guaranteed in a theory with highly curved space-time structure such as a space-time foam. The violation of such symmetry occurs through a modification of the standard quantum-mechanical evolution of matter, which is somewhat similar in nature to the behaviour characterizing open systems in stochastic media. One of the most sensitive probes for such effects is neutral kaons and other mesons. The recently completed CPLEAR experiment at CERN has sensitivity not far from the theoretically estimated magnitude of such CPT violating effects in minimal-suppression models. If the Planck energy scale minimally suppresses quantum-gravity effects, then such effects could be falsified at new experimental meson facilities, for example at Frascati in Italy and Fermilab in the US.
A second effect, which may also be falsified in the immediate future, is a sort of mean-field effect of quantum-gravity foamy situations, according to which the propagation of ordinary particles in this medium results in a modification of the particle’s dispersion relation. This effect was first predicted in the framework of Liouville strings. A similar effect has since been shown to characterize the loop-gravity approach. Modified dispersion relations have also been postulated independently at a phenomenological level by researchers proposing a thermal-like nature of the quantum gravity environment or inspired by condensed matter situations. A modification of the dispersion relation for photons or other particles with no mass implies a non-trivial refractive index in vacuo, in other words a frequency-dependent velocity of light. The origin of this effect can be traced back to the spontaneous violation of Lorentz invariance that may characterize the ground state of such theories.
Such effects are also known to describe local field theory situations in non-trivial vacua, such as thermal vacua, or quantum field theories in the vicinity of black hole backgrounds, even allowing for superluminal signals without violations of causality. However, the effect predicted by the stringy (Liouville) approach to quantum gravity has two distinctive features: the effect always leads to subluminal signals, and it is enhanced with increasing energy of the particle probe, in contradistinction to the field-theoretical cases where the effect decreases with energy. In contrast to the stringy case, the loop gravity approach predicts superluminal signals as well.
The Liouville approach to quantum gravity also predicts stochastic light-cone fluctuations. The latter have also been conjectured to characterize some non-trivial theories of local quantum gravity involving coherent gravitons. Light-cone fluctuations imply stochastic fluctuations of the speed of light in vacuo, which will imply stochastic fluctuations in the arrival times of photons of the same frequency in contrast to the refractive index effect, which implies arrival-time fluctuations for photons of different frequencies. The stochastic effect in string theory is suppressed (as compared with the refractive index effect) by powers of the (weak) string coupling expressing the strength of the interactions of string matter.
Astrophysical probes
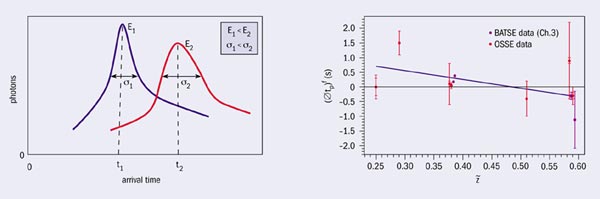
One of the first probes suggested for the experimental falsification of the refractive index and the stochastic light-cone fluctuation effects was gamma-ray bursts (GRBs). Experimental tests of such effects would look for microstructure in the arrival time of light beams from a GRB (figure 2) and a correlation with distance (redshift). If the emission of photons at various energies were simultaneous within the standard quantum mechanical limits, then a refractive index effect would imply differences in the arrival times of photons at different energies. In Liouville string models the subluminal nature of the effect implies that the higher energies would be delayed more. In contrast, loop-gravity-inspired models are characterized by both superluminal as well as subluminal propagation, and as a result there would be birefringence effects, which are absent in the stringy models. On the other hand, as far as stochastic light-cone fluctuations are concerned, there would be fluctuations in the arrival times of photons at the same energy. A systematic theoretical error analysis is needed, however, given that it is possible that photons at different energies are not emitted simultaneously.
Some of the GRBs observed so far are characterized by microstructures in their light curves of less than a millisecond, and are likely to emit gamma rays in the GeV or even TeV energy regions. Since many of these GRBs are known to be at cosmological distances (of the order of 3000 Mpc or larger), the sensitivity of these high-energy channels to the quantum-gravity refractive index and stochastic effects is such that they can be falsified with the next generation of satellite GRB-dedicated facilities, such as NASA’s Gamma-ray Large Area Space Telescope (GLAST) and the AMS experiment. Similar sensitivities might be achieved by terrestrial and extraterrestrial interferometric devices, which are also capable of detecting these stochastic quantum-gravity effects as part of the noise in the resulting interference patterns.

Other astrophysical probes of the stochastic quantum-gravity effects may be provided by ultra-high-energy cosmic rays (UHECR) with energies above 1019 eV, as well as by TeV photons. The presence of such events seems puzzling from the point of view of Lorentz invariance – standard kinematics imply the existence of energy thresholds, the Greisen, Zatsepin, Kuzmin (GZK) cut-off, above which certain reactions would prevent such energetic particles from reaching the observation point, assuming an extra-galactic origin. Some exotic suggestions have been made to relate Lorentz invariance violation associated with the quantum-gravity-induced modification of the particle’s dispersion relations with the existence of UHECR or TeV photons, in the form of an abolition of the GZK cut-off in such models.
High-energy cosmic neutrinos are also sensitive probes of quantum-gravity effects. For instance, if a minimally suppressed refractive index for neutrinos is valid, then ultra-high-energy neutrinos of 1019 eV, which may be emitted from GRBs, will be completely dispersed and thus unobservable, according to models with minimal Planck-scale suppression. The observation of such energetic particles would therefore exclude such models right away. Minimal suppression models of quantum-gravity foam with baryon-number violating interactions are in fact already excluded on the basis of solar and extra-galactic neutrino observations, since such effects would lead to neutrino oscillations in direct conflict with the experiment.
Last, but not least, bounds on stochastic effects significantly more stringent than those placed by astrophysical observations may be obtained by means of atomic physics experiments. Such experiments are mainly concerned with measurements of quantum-gravity induced corrections to the gyromagnetic ratio of charged particles, which can be measured with high accuracy.
In summary, a plethora of relatively low-energy measurements can be made, some of which are already on the verge of excluding Planckian physics models. Any future experimental attempt to bind models of quantum gravity should therefore be encouraged, since they present the only way to arrive at a true theory of quantum gravitation, which will probably lead to a better understanding of the structure of space-time itself. The concept of a phenomenology of quantum gravity may soon no longer be considered oxymoronic.
Further reading
R Adler et al. 1995 CPLEAR collaboration Phys. Lett. B364 239.
G Amelino-Camelia et al. 1998 Nature 393 763 (astro-ph/9712103 at http://www.arxiv.org/).
J Ellis, N E Mavromatos and D V Nanopoulos 1993 Erice Subnucl. Series 31 1 (hep-th/9304133 at http://www.arxiv.org/).
J Ellis, K Farakos, N E Mavromatos, V Mitsou and D V Nanopoulos 2000 Astrophys. J. 535 139.
J Ellis, N E Mavromatos and D V Nanopoulos 2000 Phys. Rev. D62 084019 (gr-qc/0006004 at http://www.arxiv.org/).
R Gamibini and J Pullin 1999 Phys. Rev. D59 124021. (gr-qc/9809038 at http://www.arxiv.org/).
R Gamibini and J Pullin 2001 gr-qc/0110054 at http://www.arxiv.org/.
L J Garay 1999 Int. J. Mod. Phys. A14 4079 (gr-qc/9911002 at http://www.arxiv.org/).
L Gonzalez-Mestres 1997 physics/9704017 at http://www.arxiv.org/.
Hong-wei Yu and L H Ford 1999 Phys. Rev. D60 084023 (gr-qc/9904082 at http://www.arxiv.org/).
N E Mavromatos 2000 Dark matter in astro and particle physics Proc. Heidelberg 2000 209 ed. H V Klapdor-Kleingrothaus (Springer, Berlin) (gr-qc/0009045 on http://www.arxiv.org/).
Subir Sarkar 2002 gr-qc/0204092 on http://www.arxiv.org/.





